What is called a Spring & Resilience?
A spring is a mechanical device used to store energy and subsequently to release it in need. The energy stored in the spring is called its resilience.
Springs are of two types –
- Leaf spring – A leaf spring is made up of elastic material shaped into flat rectangular leaf. One or more leaves are used together. Leaves are manufactured and shaped with initial bend in the opposite direction of loading. This is called initial camber. When the spring is loaded, spring leaf suffers bending moment. Hence, their characteristics depends upon Young’s modulus.
- Coil spring – Coil spring is made up of an elastic material and formed into the shape of a helix. When the spring is loaded, its coils undergo torsional stress. Hence, their characteristics depends upon Shear modulus.
Coil springs are further classified into two types –
- Close coiled springs – In this type of spring, the wire rounds of helix are wound closely packed with no space between coils. This type of spring is used where tensile loads are acting. The spring elongates on loading and returns to its normal length when unloaded.
- Open coiled springs – In this type of spring, the wire rounds of helix are wound with space between coils. It is used where compressive loads are acting. The spring shortens on loading and returns to its normal length when unloaded.
Use of Springs
Springs are used for the following purposes –
- Leaf springs are used in the suspension system of road vehicles such as cars, buses, trucks etc.
- Coil springs are mostly used in the primary suspension system of heavy vehicles such as railway coaches and wagons etc.
- Springs used in the suspension system of machine beds which are subjected to vibrations.
- Coil springs are used in damping system to absorb shocks.
- Spring is also used to maintain a force between two contacting surfaces such as in carbon brushes of generators, motors etc.
Vibrations of Springs
In this article we will discuss in detail about vibrations in coil springs.
When a body or mass is suspended with a coil spring and is set into vibrations, body undergoes oscillations which are simple harmonic motions.
Horizontal Oscillations
Consider about a mass-less spring lying on a friction less horizontal table as shown in figure. One end of the spring is attached to a rigid support and other end is attached with a body of mass ( m ) .
If the body is further pulled towards right for a small distance ( x ) and released, it will start oscillating “to and fro” about its equilibrium position.
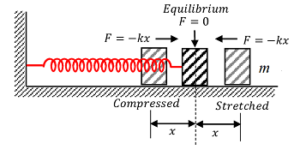
Restoring force acting on the mass body is ( F = - k x ) . Here, ( k ) is the force constant of spring.
The negative sign indicates that the force ( F ) is acting opposite to the direction of displacement ( x ) .
From definition of a force –
F = m a
Hence, \quad m a = - k x
Therefore, acceleration of mass will be –
a = - \left ( \frac { k }{ m } \right ) x
From above equation it is clear that, motion of the mass possess following characteristics –
- It is moving “to and fro” along the axis of the spring.
- Acceleration ( a \propto x ) Because ( k ) \ \text {and} \ ( m ) are constants.
- Acceleration, ( a ) is acting in a direction opposite to the direction of displacement ( x ) .
These are the required conditions of a simple harmonic motion. Hence, the motion of mass ( m ) is simple harmonic motion.
Therefore, we can write for simple harmonic motion –
\left ( \frac { k }{ m } \right ) = \omega ^ 2
Hence, time period of the motion will be –
T = \left ( \frac { 2 \pi }{ \omega } \right ) = 2 \pi \sqrt { \frac { m }{ k }}
And frequency of oscillations will be –
\nu = \left ( \frac { 1 }{ T } \right ) = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k }{ m }}
Vertical Oscillations
Consider about a mass-less spring suspended vertically from a rigid support with a body of mass ( m ) attached at other end as shown in figure. Due to the weight of the mass, the spring is stretched down to a distance ( d ) .
Due to elasticity of the spring a restoring force will act in upward direction. For equilibrium of mass –
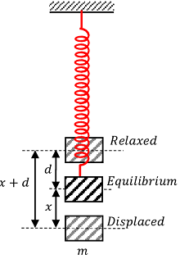
m g = k d
If the body is further pulled vertically downwards for a small distance ( x ) from its equilibrium position and released, it starts oscillating “up and down” about its equilibrium position.
Therefore, the resultant force acting on the body is –
F = m g - k ( d + x ) = k d - k d - k x = - k x
Or, \quad F = - k x
If, ( a ) is the linear acceleration of vertical oscillations of the mass. Then –
a = - \left ( \frac {k}{m} \right ) x
This is the required condition of a simple harmonic motion. Therefore, motion of mass ( m ) is a simple harmonic motion.
Obviously, the gravitational force has no effect on the force constant ( k ) and time period ( T ) of the oscillations.
Parallel combination of Spring
In a combination of springs, if one end of all the springs are connected with the mass body and other ends are connected to the supports, then it is called a parallel combination of springs.
- Figure (A) shows parallel combination of two springs for horizontal oscillations.
- Figure (B) shows parallel combination of two springs for vertical oscillations.
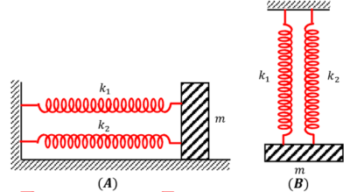
In parallel combination of springs, force ( F ) is different for different springs. But extension ( y ) is same for all springs.
Let, ( k _ 1 ) and ( k _ 2 ) are the spring constants and ( y ) be the extension produced in each spring. Therefore, restoring force produced in two springs will be –
( F _ 1 = k _ 1 y ) \quad and \quad ( F _ 2 = k _ 2 y )
Therefore, total restoring force is –
F = ( F _ 1 + F _ 2 ) = - \left ( k _ 1 + k _ 2 \right ) y ……… (1)
Let, ( k _ p ) is the equivalent spring constant for parallel combination of springs then –
F = k _ p y ………. (2)
Comparing equations (1) and (2), we will get –
k _ p = ( k _ 1 + k _ 2 )
Therefore, frequency of vibrations of parallel combination of springs will be –
\nu _ p = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k _ p }{ m }}
Or, \quad \nu_p = \left ( \frac { 1 }{ 2 \pi } \right ) \sqrt { \frac { k _ 1 + k _ 2 }{ m }}
Series combination of Spring
In a combination of springs if one end of first spring is connected with support and other end is connected with one end of second spring while other end of the last spring is connected to the vibrating mass body and remaining all other intermediate springs are connected end to end, then it is called a series combination of springs.
- Figure (A) shows series combination of two springs for horizontal oscillations.
- Figure (B) shows series combination of two springs for vertical oscillations.
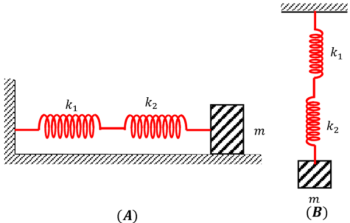
In series combination of springs, force ( F ) is same for all springs. But, extension or compression ( x ) is different for different springs.
Let, ( x _ 1 ) and ( x _ 2 ) are the extension or compression produced in individual springs. Restoring force for springs –
F = - k _ 1 x _ 1 = - k _ 2 x _ 2
Therefore, \quad x _ 1 = - \left ( \frac { F }{ k _ 1} \right ) . And \quad x _ 2 = - \left ( \frac { F }{ k _ 2 } \right )
Total extension of springs –
x = ( x _ 1 + x _ 2 )
Therefore, \quad x = \left [ - \left ( \frac { F }{ k _ 1 } \right ) - \left ( \frac { F }{ k _ 2 } \right ) \right ]
Or, \quad x = - F \left [ \left ( \frac { 1 }{ k _ 1} \right ) + \left ( \frac { 1 }{ k _ 2 } \right ) \right ] …….. (3)
Let, ( k _ s ) is the equivalent spring constant for the series combination. Then, \quad F = - k_s x
Or, \quad x = - F \left ( \frac {1}{k_s} \right ) ……….. (4)
Comparing equations (3) and (4), we will get –
\left ( \frac {1}{k _ s} \right ) = \left ( \frac {1}{k _ 1} \right ) + \left ( \frac {1}{k _ 2 } \right )
Or, \quad k_s = \left ( \frac {k_1 k_2}{k_1 + k_2} \right )
See numerical problems based on this article.
