Laws of Friction

What are Laws of Friction?

Friction is a natural phenomenon which resists the motion of a solid material body upon another solid surface or liquid mass or gaseous atmosphere. Therefore, if there is a relative motion between two surface, a frictional force is developed on the body surface in a direction opposite to the direction of movement of the body. Frictional force comes to play in action when any solid body moves or tend to move (1) upon another solid surface (2) in a liquid mass or (3) in a gaseous atmosphere. Frictional force also occurs when, one liquid layer slides or tends to slide over another layer.

Different laws have been formulated for analyzing the force of friction. Force of friction has five basic laws. These are –

1. First Law – When a body is moving on a surface, frictional force is directly proportional to the normal reaction on the surface of contact. Its direction is tangential to the surface of contact and act opposite to direction of movement.
2. Second Law – Friction doesn’t depend upon the area of contact between bodies.
3. Third Law – The co-efficient of static friction is slightly higher than the value of co-efficient of kinetic friction.
4. Fourth Law – Kinetic friction is independent of the velocity of a moving body.
5. Fifth Law – Friction depends upon the nature of surfaces in contact.

To be Noted –

Laws of friction are purely experimental and there is no mathematical proof for them.

Coefficient of Friction

According to the first law of friction –

When a body is moving on a surface, frictional force is directly proportional to the normal reaction to the surface of contact and its direction is tangential to surface and acting opposite to the direction of movement.

Consider about a solid block resting on a horizontal plane surface AB as shown in figure. Let, a pulling force ( P ) is applied on the block to move it. But the block remains in rest due to friction force.

If the pulling force is just enough such that, the block is just about to move, then developed frictional force ( f ) will act tangential to the surface of contact in a direction opposite to the tendency of movement of block. In this situation, the frictional force ( f ) acting on the block is limiting frictional force.

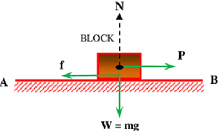
Let, ( N ) is the normal reaction acting on the surface of contact. Since plane AB is horizontal, therefore normal reaction N is equal to the weight ( mg ) of the block.

First law of friction states that, frictional force is directly proportional to the normal reaction.

Therefore, \quad \left ( \frac {f}{N} \right ) = \text {Constant} . This constant is called coefficient of friction. It is denoted by ( \mu )

Thus, coefficient of friction \quad \mu = \left ( \frac {f}{N} \right )             

Therefore, coefficient of friction can be defined as the ratio of frictional force to normal reaction for a given pair of surfaces in contact.

How value of Coefficient of Friction varies?

Value of co-efficient of friction depends upon –

1. Nature of body materials in contact.
2. Surface roughness of bodies in contact.

Value of co-efficient of friction doesn’t depends upon –

1. Area of contact between a given pair of bodies.
2. Acceleration due to gravity ( g ) .

For clear understanding of these facts, let us consider about an illustrative example discussed below.

Consider about the figure shown below. A wooden rectangular block A is kept on a plane surface. Let, length, breadth and height of block are ( l ), \ ( b ) \ \text {and} \ ( h ) respectively. Let, ( l > b > h ) .

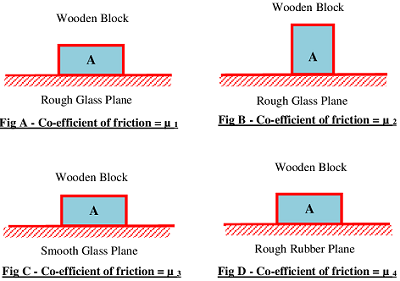
Now consider about placement of block on different surfaces in different manner –

Figure (A) – The wooden block A is placed on a rough glass plane surface. In this figure, major dimensions of the block are in contact i.e. major surface area \left ( l \times b \right ) of the block is in contact with glass plane surface. Assume that the co-efficient of friction for this combination of surfaces is ( \mu_1 ) and developed force of friction is ( f_1 )

Figure (B) – The same wooden block A is now placed on same rough glass plane surface. At this time the minor dimensions are in contact i.e. minor surface area \left ( b \times h \right ) of block is in contact with glass plane surface. Assume that the co-efficient of friction for this combination of surfaces is ( \mu_2 ) and developed force of friction is ( f_2 )

Figure (C) – The same wooden block A is now placed on another glass plane surface which is smooth. Again the major dimension i.e. major surface area \left ( l \times b \right ) is in contact with the glass plane. Assume that co-efficient of friction for this combination of surfaces is ( \mu_3 ) and developed force of friction is ( f_3 )

Figure (D) – The block A is now placed on a rough rubber plane surface. Again major dimension i.e. major surface area \left ( l \times b \right ) is in contact with the rubber plane. Let co-efficient of friction for this combination of surfaces is ( \mu_4 ) and developed force of friction is ( f_4 )

OBSERVATION – 1

Comparing between situations in figure (A) and (B) we have –

1. Nature of contact surfaces are same.
2. Area of contact surfaces are different.
3. Mass or weight of the body is same.

According to laws of friction, we have following observations –

1. ( \mu_1 ) = ( \mu_2 ) Because coefficient of friction depends upon the nature of material of two bodies in contact.
2. ( f_1 = f_2 ) Because friction doesn’t depend upon the area of contact. It only depends upon the mass of body i.e. normal reaction. Mass is not changing if the body is kept either with minor dimensions or major dimensions in contact with glass plane.

OBSERVATION – 2

Comparing between situations in figure (A) and (C) we have –

1. Nature of contact surfaces are different due to difference in surface roughness.
2. Area of contact surfaces are same.
3. Mass or weight of the body is same.

According to laws of friction, we have following conclusions –

1. ( \mu_3 ) < ( \mu_1 ) Because coefficient of friction depends upon roughness of surfaces in contact. Smooth glass surface has low roughness than rough glass.
2. ( f_3 < f_1 ) Due to decrease in coefficient of friction for smooth glass surface friction force has decreased.

OBSERVATION – 3

Comparing between situations in figure (A) and (D), we have –

1. Nature of contact surfaces are different due to different materials in contact.
2. Area of contact surfaces are same.
3. Mass or weight of the body is same.

According to laws of friction, we have following conclusions –

1. ( \mu_4 ) > ( \mu_1 ) Because coefficient of friction depends upon nature of material of surfaces in contact. Rubber has more coefficient of friction as compared to glass.
2. ( f_4 > f_1 ) Due to increase in coefficient of friction for rubber friction force has increased.

OBSERVATION – 4

Comparing between situations in figure (C) and (D) we have –

1. Nature of contact surfaces are different due to difference in materials in contact.
2. Area of contact surfaces are same.
3. Mass or weight of the body is same.

According to laws of friction, we have following conclusions –

1. ( \mu_4 ) > ( \mu_3 ) Because coefficient of friction depends upon nature of material of surfaces in contact. Rubber has more coefficient of friction as compared to glass.
2. ( f_4 > f_3 ) Due to increase in coefficient of friction for rubber friction force has increased.

Value of Coefficient of Friction may be greater than 1

Almost for all surfaces, co-efficient of friction is less than 1 .

Therefore, \quad ( \mu < 1 )

For a given pair of surfaces in contact, value of frictional force ( f ) is always less than value of normal reaction ( N ) . Therefore, for most of contact surfaces ( f < N )

In very rare cases, value of co-efficient of friction is found greater than unity. In this case frictional force is higher than normal reaction.

Example – Silicon rubber has value of co-efficient of friction ( \mu ) much greater than 1 .

Angle of Friction

Consider about a body of mass ( m ) which is resting on a rough plane surface AB as shown in figure. Body is applied with a pulling force ( P ) just to move on the plane.

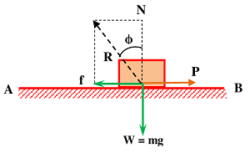
In limiting conditions, the body will be in equilibrium under the action of the following forces.

1. Weight of body ( W = mg ) ( Acting vertically downward. )
2. Pulling force ( P ) ( Acting horizontal. )
3. Normal reaction ( N ) ( Acting perpendicular to the contact surface. )
4. Frictional force ( f ) ( Acting opposite to the tendency of movement of body. )

Now, normal reaction ( N ) acting on the surface is –

N = ( mg )

Let, ( R ) is the resultant of normal reaction ( N ) and frictional force ( f ) . Let, it makes an angle ( \phi ) with normal reaction ( N ) in positive direction.

Angle of friction or Angle of repose is the angle made in positive direction by the resultant ( R ) with the normal ( N ) .

By completing parallelogram with sides ( f ) and ( N ) we have –

\tan \phi = \left ( \frac {f}{N} \right )

But, \quad \mu = \left ( \frac {f}{N} \right ) From definition of co-efficient of friction.

Therefore, \quad \mu = \tan \phi

Thus, tangent of angle of friction ( \phi ) is equal to co-efficient of friction ( \mu ) .

See numerical problems based on this article.

• P020106
• P020107
• P020108
• P020109
• P020110
• P020111
• P030121