Reflection of Waves

What are effects of boundary in Reflection of Waves?

When a progressive wave comes in contact with a boundary interface, then reflection of waves or refraction occur depending upon the nature of boundary conditions. 

Reflection or refraction of a wave mainly depends upon two factors. These are (1) Boundary conditions and (2) Medium.

(1) Boundary conditions – This is of two types.

1. Rigid boundary – It is a fixed and rigid boundary incapable to move such as a wall, tree etc.
2. Open boundary – It is a boundary which is free to move, flexible or open such as a diaphragm, movable ring or open atmosphere etc.

(2) Medium of propagation – This is of two types.

1. The medium which offers less resistance to the propagation of a wave is called Rarer medium.
2. The medium which offers high resistance to the propagation of a wave is called Denser medium.

TO BE NOTED –

1. Rarer or denser medium are only comparative features between two mediums through which a wave travels.
2. If a wave is travelling in one medium enters into another medium then the medium which has comparatively lighter density is referred as a rarer medium and the other medium is referred as denser medium.

Reflection of Waves from Rigid boundary

Consider about a crest of a wave which is travelling through a string AB as shown in figure. The string is attached to a rigid support such as a wall.

Here, the density of string is lighter than wall. Hence, string behaves as rarer medium and the wall behaves as a denser medium.

As the pulse reaches the wall, it exerts an upward force on the wall. By Newton’s third law of motion, the wall will exert an equal downward force on the string. This will produce a reflected pulse in the downward direction i.e. a trough of wave will generate which travels through the string in reverse direction.

Thus a crest is reflected back as a trough.

Therefore, when a travelling wave is reflected from a rigid boundary, it is reflected back with a phase difference of ( \pi ) radians.

If the incident wave is represented by the equation –

y_i = A \sin ( \omega t - k x )

Then the reflected wave will be represented by the equation –

y_r = - A \sin ( \omega t + k x )

Sign of ( y ) is changing because phase is changing by ( \pi ) sign of ( x ) is changing because direction of wave motion has reversed after reflection.

At the boundary, the incident pulse and the reflected pulse meet in opposite phases and so they cancel to each other. The amplitude of transverse vibration will be zero at this point. At the boundary interface, the net displacement is zero.  This point is called a node.

Reflection of Waves from Open boundary

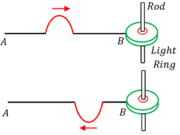
Consider about a crest of wave which is travelling through a string as shown in figure. The string is attached to a light ring which can slide up and down on a friction-less vertical rod.

Here, the string with light ring behaves as rarer medium and the rod behaves as a denser medium for the wave.

As the pulse reaches the end B  it meets no any resistance and exerts an upward force on the ring. The ring rises above its equilibrium position. As the ring moves up it stretches the string and produces a reflected pulse in the upward direction which travels back through the string as crest.

Thus a crest is reflected back as a crest.

Therefore, when a travelling wave is reflected from a free and flexible or open boundary, it is reflected back with no phase difference.

If the incident wave is represented by the equation –

y_i = A \sin ( \omega t - k x )

Then the reflected wave will be represented by the equation –

y_r = A \sin ( \omega t + k x )

Only sign of ( x ) is changing because the direction of wave motion has reversed but phase remains the same.

1. At the boundary, the incident pulse and the reflected pulse meet in same phases and so they added to each other. The amplitude of transverse vibration will be maximum at this point.
2. At the boundary interface, the displacement is maximum. This is called an antinode. Here, the amplitude is twice of the amplitude of either of pulses.

Refraction of Waves

Consider about a combination of a thin string A and a thick string B kept under the same tension as shown in figure.

Since, string A is thin its mass per unit length will be low. Hence, the wave travels faster in string A as compared to the string B . Therefore, string A acts as a rarer medium.

Refraction of Waves into Denser medium

Suppose a wave crest is moving from string A towards string B as shown in figure. The wave is moving from rarer medium to denser medium.

At the interface, it will partly refracted into string B and partly reflected back in string A at the interface. The reflected pulse travels back in string A and moves faster. It suffers a phase change of ( \pi ) radians similar to that of reflection from a rigid boundary discussed earlier.

The refracted pulse travels in string B and moves slower due to entering in denser medium. It does not suffer any phase change.

Refraction of Waves into Rarer medium

Suppose a wave crest is moving from string B towards string A as shown in figure. The wave is moving from denser medium to rarer medium.

At the interface, it will partly refracted into string A and partly reflected back into string B . The reflected pulse travels back in string B and moves slower. It does not suffer any phase change similar to that of reflection from open boundary discussed earlier.

The refracted pulse travels in string A and moves faster due to rarer medium. It does not suffer any phase change. From above discussions, it is narrated that –

A wave suffers no phase change during its refraction from one medium to another medium.