Buoyancy

What is called Buoyancy?

The upward force acting on a immersed body in a fluid is called upthrust or buoyant force and the phenomenon is called buoyancy.

The force of buoyancy acts through the centre of gravity of the fluid displaced by body which is called centre of buoyancy.

When a body is immersed in a fluid, the fluid exerts pressure on all faces of that body. This fluid pressure is called thrust which increases with depth of liquid. The upward thrust at the bottom is more than the downward thrust on the top. Because, the bottom face is at the greater depth than the top face. Hence, a resultant upward force acts on a body.

EXAMPLE –

A cork taken inside water experiences an upward thrust and comes to the surface due to buoyancy.
Similarly, while drawing water from a well, a bucket is found too much lighter when it is inside water than when it comes out of water.

Archemedes’ principle of buoyancy

Archemedes’ principle states that –

When a body is partially or fully immersed in a fluid, it will experience an upward thrust which is equal to the weight of the fluid displaced by that body. The upthrust acts through the centre of gravity of the displaced fluid.

Therefore, Archemedes’ principle is consists of the following statements –

When a body is partially or wholly immersed in a fluid it will experience an upward thrust which develops due to pressure exerted by the fluid.
When the body is immersed in fluid it will displace some fluid whose volume is equal to the volume of the body part immersed in the fluid.
The upward thrust exerted on body is equal to the weight of the volume of fluid displaced by that body.
The upthrust always acts through the centre of gravity of the displaced fluid.

This principle was discovered by the great Greek scientist Archimedes around 225 B.C and it gives the magnitude of buoyant force on a body.

Buoyant Force or Upthrust

Consider about a rectangular body of height $( h )$ lying inside a liquid mass of density $( \rho )$ at a depth $( x )$ below the free surface of the liquid as shown in figure.

Let, the area of cross section of body is $( a )$ .

Pressure at the upper face of the body will be –

$P_1 = x \rho g$

Therefore, thrust acting on the upper face of the body is –

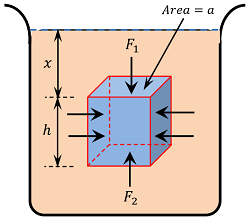
BUOYANCY & ARCHEMEDES' PRINCIPLE — 130701 BUOYANCY & ARCHEMEDES’ PRINCIPLE

$F_1 = P_1 a = x \rho g a \quad$ ( This is acting vertically downwards ).

Similarly, pressure at the lower face of the body will be –

$P_2 = (x + h ) \rho g$

Therefore, thrust acting on the lower face of the body is –

$F_2 = P_2 a = (x + h ) \rho g a \quad$ ( This is acting vertically upwards ).

The forces on the two side faces of the body will cancel to each other because they are of identical shape, size and are at same depth.

Since, the depth of the lower face is more than the depth of upper face, so $\quad (F_2 > F_1 )$

Thus, resultant force acting on the body is $( F_2 - F_1 )$

This thrust is acting on the body in the upward direction and is called upthrust $( U )$ .

Therefore, $\quad U= ( F_2 - F_1 )$

$= ( x + h ) \rho g a - x \rho g a$

$= a h \rho g$

But, $\quad a h = V$ ( Volume of the body )

Also volume of liquid displaced by the body will be $( V )$

Therefore, $\quad U = V \rho g = M g$

Since, $\quad V \rho = M$ ( Mass of liquid displaced ).

So, $\quad \text {Upthrust or buoyant force} = \text {Weight of liquid displaced}$

This proves the Archemedes’ principle.

Apparent weight of an immersed body

When a body is partially or fully immersed in a fluid, it will experience some loss in its weight. This loss in weight is in accordance with the Archemedes’ principle. Hence, the weight of a body immersed in a fluid is called apparent weight.

The actual weight $( W )$ of the immersed body acts downwards and the upthrust $( U )$ acts upwards.

Let –

$\rho =$ density of body material.
$\sigma =$ density of fluid.

We know that –

$\text {Apparent weight} = ( \text {Actual weight} - \text {Buoyant force} )$

Therefore, $\quad W_{app} = W - U$

$= V \sigma g - V \rho g$

$= V \sigma g \left ( 1 - \frac {\rho}{\sigma} \right )$

$= W \left ( 1 - \frac {\rho}{\sigma} \right )$

If the values for $( W ) \ \text {and} \ ( \sigma )$ are known, the value of density $( \rho )$ of a body can be obtained by using this equation.

Laws of flotation

Laws of flotation states that –

A body will float in a liquid if the weight of displaced liquid by the immersed part of the body is equal to or greater than the weight of body.

Explanation –

When a body is immersed fully or partially in a liquid the following two vertical forces act upon it –

True weight $( W )$ which acts vertically downwards through its centre of gravity.
Force of buoyancy or upthrust $( U )$ which acts vertically upwards through the centre of buoyancy.

Depending upon the values of $( W )$ and $( U )$ three conditions are possible –

Weight of body is greater than upthrust exerted by liquid i.e. $( W ) > ( U )$
Weight of body is equal to the upthrust exerted by liquid i.e. $( W ) = ( U )$
Weight of body is lower than upthrust exerted by liquid i.e. $( W ) < ( U )$

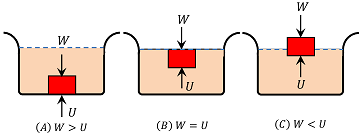
(A) When weight of body is greater than upthrust ( W > U )

The weight of the body is higher than the upthrust.

The net force $( W - U )$ acts in the downward direction. Hence, the body sinks.

$W > U$

Or, $\quad V \sigma g > V \rho g$

Or, $\quad \sigma > \rho$

Thus a body sinks in a liquid if its density is greater than the density of the liquid.

Example – An iron piece or a stone sinks in water.

(B) When weight of body is equal to the upthrust ( W = U )

The weight of the body is just balanced by the upthrust. No net force acts on the body. The body floats in fully immersed condition.

$W = U$

Or, $\quad V \sigma g = V \rho g$

Or, $\quad \sigma = \rho$

Example – A drop of olive oil stands at rest anywhere in a mixture of equal quantities of water and alcohol because, the density of olive oil is equal to that of the mixture.

(C) When weight of body is lower than upthrust ( W < U )

The gravitational force or weight of body, $( W )$ is less than the upward force $( U )$ . The body floats partly immersed in liquid. This is because, the body sinks only to the extent at which $( W = U )$ .

Here, $( \sigma < \rho )$ . The density of the floating body is less than the density of fluid.

Example – A piece of cork floats on water.

Fraction of submerged volume

We know that, when weight of body is less than the weight of the liquid displaced the body floats partially submerged under the liquid surface.

Let –

$V =$ Volume of body.
$V' =$ Volume of submerged part of body. This volume is also called wetted volume.

Then for equilibrium of body –

$\text {Weight of the body} = \text {Weight of liquid displaced}$

So, $\quad V \sigma g = V' \rho g$

Or, $\quad \left (\frac {V'}{V} \right ) = \left (\frac {\sigma}{\rho} \right )$

Hence, $\quad \left ( \frac {\text {Volume of submerged part}}{\text {Total volume of body}} \right ) = \left ( \frac {\text {Density of body}}{\text {Density of liquid}} \right )$

Examples of floating bodies

A ship is made of steel which is 8 times denser than water. But the interior of ship is made hollow by giving it a concave shape so that, it can displace much more water than its own weight. So the ship floats and can carry a lot of cargo due to buoyancy.
Ice floats on water because the density of ice is less than that of water.
Human body is slightly denser than water. An inflated rubber tube has low weight and large volume and increases the upthrust. It helps a person to float in water.
A person can swim in sea water more easily than in river water. The density of sea water is more than that of river water and so it exerts a greater upthrust.
The average density of a fish is slightly greater than water. Fishes have an anatomical attachment called swim bladder whose size they can adjust. With the help of this bladder, the fish is able to swim in water with ease.

See numerical problems based on this article.