What is a spherical Capacitor?
A capacitor consisting of two concentric spherical shells is called a spherical capacitor.
Electric Field between spherical surfaces
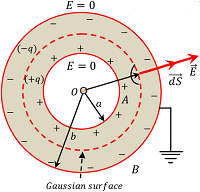
Consider a spherical capacitor as shown in figure. Let,
- Concentric inner and outer spherical shells are ( A ) \ \text {and} \ ( B ) respectively.
- Radii of shells are ( a ) \ \text {and} \ ( b ) .
- Charge on inner shell is ( + q ) and outer shell is ( - q ) .
- The outer shell is earthed.
A Gaussian surface is drawn as shown in figure in dotted circle. Let, the radius of the spherical Gaussian surface is ( r ) . Then, according to Gauss law –
\oint \vec {E} . d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
Because, ( \vec {E} ) and ( \vec {S} ) are along the same line, so ( \theta = 0 \degree ) . Therefore, \quad \oint \vec {E} . d \vec {S} = \oint E . d S \cos 0 \degree = \oint E . dS
Or, \quad \oint E . dS = \left ( \frac {q}{\epsilon_0} \right )
Since, ( E ) is uniform over the Gaussian surface due to symmetry. So, \quad E \oint d S = \left ( \frac {q}{\epsilon_0} \right )
Also, \quad \oint d S = \left ( 4 \pi r^2 \right ) ( Surface area of Gaussian surface ). Therefore, \quad E \times \left ( 4 \pi r^2 \right ) = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right ) ……….. (1)
Thus, intensity of electric field at a point of spherical capacitor is – (1) Proportional to the charge on the spherical surface and (2) inversely proportional to the square of the distance of point from the centre of spheres.
Potential difference between spherical surfaces
From relation between electric field and potential difference, we get –
\vec E = - \left ( \frac {dV}{\vec {dr}} \right )
Or, \quad dV = - \vec {E} \ ( \vec {dr} )
By integration, we get –
V = - \int\limits_{b}^{a} \vec {E} . d \vec {r}
Since, ( \vec {E} ) and ( \vec {r} ) are along the same line. So, \quad \vec {E} . d \vec {r} = E. dr \cos 0 \degree = E dr
Therefore, \quad V = - \int\limits_{b}^{a} E. dr = - \int\limits_{b}^{a} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2} \right ) dr
= \left ( \frac {- q}{4 \pi \epsilon_0} \right ) \int\limits_{b}^{a} r^{(- 2)} dr
= \left ( \frac {- q}{4 \pi \epsilon_0} \right ) \left [ \frac {r^{(-1)}}{(-1)} \right ]_{b}^{a}
= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {1}{r} \right ]_{b}^{a}
= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {1}{a} - \frac {1}{b} \right ]
= \left [ \frac {q ( b - a )}{4 \pi \epsilon_0 ab} \right ]
= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {( b - a )}{ab} \right ] ……….. (2)
Thus, potential difference between spherical surfaces is – (1) Proportional to the charge on the spherical surface and (2) proportional to the difference of inverse of radii of the spheres.
Capacitance of spherical Capacitor
By equation (2), the capacitance of spherical capacitor will be –
C = \left ( \frac {q}{V} \right )
= \left [ \frac {q}{\frac {q ( b - a )}{4 \pi \epsilon_0 ab}} \right ]
= \left [ \frac {4 \pi \epsilon_0 q ab}{q ( b - a )} \right ]
= 4 \pi \epsilon_0 \left [ \frac {ab}{( b - a )} \right ]
Therefore, capacitance of an spherical capacitor only depends upon the inner and outer radii of spheres.
Cylindrical Capacitor
A capacitor consisting of two concentric cylinders is called a cylindrical capacitor.
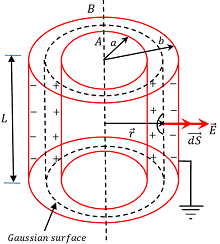
Consider a cylindrical capacitor as shown in figure. Let, –
- Inner and outer cylindrical shells of capacitor are ( A ) \ \text {and} \ ( B ) .
- Length of cylinders are ( L ) and radii are ( a ) and ( b ) respectively.
- Inner cylinder surface charge is ( + q ) and outer cylinder surface charge is ( - q ) .
- The outer cylindrical surface is earthed as shown in figure.
Electric Field between cylindrical surfaces
A Gaussian surface is drawn as shown in figure. According to Gauss law –
\oint \vec {E} . d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
So, \quad \oint E . d S \cos 0 \degree = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad \oint E. dS = \left ( \frac {q}{\epsilon_0} \right )
Since, ( \vec {E} ) and ( \vec {S} ) are along the same line, so ( \theta = 0 \degree )
Also, ( E ) is uniform over the Gaussian surface. So, \quad E \oint d S = \left ( \frac {q}{\epsilon_0} \right )
But, \quad \oint d S = \left ( 2 \pi r L \right ) (Area of curved surface of Gaussian cylinder).
Therefore, \quad E \times \left ( 2 \pi r L \right ) = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {q}{2 \pi \epsilon_0 r L} \right ) ………. (1)
Thus, intensity of electric field at a point of cylindrical capacitor is – (1) Proportional to the charge on the cylindrical surface and (2) inversely proportional to the distance of point from the centre of spheres and length of cylinder.
Potential difference between cylindrical surfaces
The potential difference between two cylindrical shells of radii ( a ) and ( b ) with charge ( + q ) and ( - q ) respectively is given by –
V = - \int\limits_{b}^{a} E . d r = \left ( \frac {q}{2 \pi \epsilon_0 L} \right ) \int\limits_{a}^{b} \frac {dr}{r}
= \left ( \frac {q}{2 \pi \epsilon_0 L} \right ) \left [ \log_e r \right ]_{a}^{b}
= \left ( \frac {q}{2 \pi \epsilon_0 L} \right ) \left [ \log_e b - \log_e a \right ]
Therefore, \quad V = \left ( \frac {q}{2 \pi \epsilon_0 L} \right ) \log_e \left ( \frac {b}{a} \right ) ……. (2)
Capacitance of cylindrical Capacitor
Using equation (2), capacitance of a cylindrical capacitor will be –
C = \left ( \frac {q}{V} \right )
= \left [ \frac {q }{\frac {q}{2 \pi \epsilon_0 L} \log_e \left ( \frac {b}{a} \right )} \right ]
= \left [ \frac {2 \pi \epsilon_0 L}{\log_e ( b / a )} \right ]
= \left [ \frac {2 \pi \epsilon_0 L}{2.303 \log_{10} ( b / a )} \right ] ……… (3)
Therefore, capacitance of a cylindrical capacitor only depends upon the length and inner and outer radii of cylindrical shells.
