10-Numerical Problems

“Material Strength” Numerical Problems

Try to solve the following “Material Strength” numerical problems to clear the concepts in solving the numerical problems.

First of all go to the theory portion of the respective topic and then try to solve the numerical problems by yourself. If facing problem in solving the numerical, click on the Go to solution button to see the ready made solution placed at the bottom of each numerical problem.

01. PROBLEM – P100101

Find the centre of gravity of $Z$ section as shown in figure below.

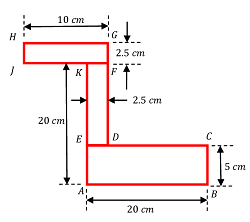
MOMENT OF INERTIA OF Z SECTION — PROBLEM FIGURE P100101

Go to solution –

Keywords related to this problem.

02. PROBLEM – P100102

A square hole is punched out of a circular lamina, the diagonal of the square being the radius of the circle as shown in figure.

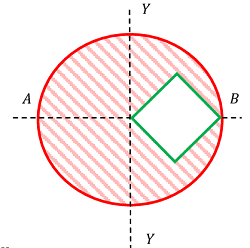
MOMENT OF INERTIA OF CIRCULAR SECTION — PROBLEM FIGURE P100102

Find the centre of gravity of remainder section if $( r )$ is the radius of circle.

Go to solution –

Keywords related to this problem.

03. PROBLEM – P100103

A frustum of a solid right circular cone has an axial hole of $( 50 \ cm )$ diameter as shown in figure.

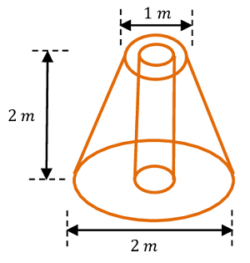
MOMENT OF INERTIA OF A TRUNCATED SOLID CONE — PROBLEM FIGURE P100103

Determine the centre of gravity of the body.

Go to solution –

Keywords related to this problem.

04. PROBLEM – P100104

Two halves of a round homogeneous cylinder are held together by a thread wrapped round the cylinder with two weights, each equal to $( P )$ , attached to its ends as shown in figure. The complete cylinder weighs $( W \ kgf )$ . The plane of contact of both of its halves is vertical.

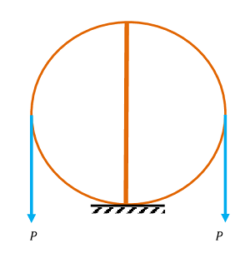
FRICTION BETWEEN TWO CYLINDRICAL HALVES — PROBLEM FIGURE P100104

Determine the minimum value of $( P )$ for which both halves of the cylinder will be in equilibrium on a horizontal plane.

Go to solution –

Keywords related to this problem.

05. PROBLEM – P100105

Three masses of $( 3 ), \ ( 4 ) \ \& \ ( 5 ) \ kg$ are located at the corners of an equilateral triangle of side $( 1 \ m )$ as shown in figure. Locate the centre of mass of the system.

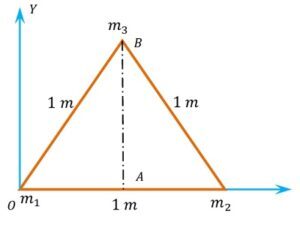
CENTRE OF MASS OF THREE POINT MASSES — PROBLEM FIGURE P100105

Go to solution –

Keywords related to this problem.

Centre of mass.

06. PROBLEM – P100106

A small sphere of radius $( R )$ is held against the inner surface of a larger sphere of radius $( 6 R )$ . The masses of larger sphere and smaller sphere are $( 4 M )$ and $( M )$ respectively. This arrangement is placed on a horizontal table. There is no friction between any surfaces of contact. The small sphere is now released. Find the co-ordinates of the centre of the larger sphere when the smaller sphere reaches the other extreme position?

Go to solution –

Keywords related to this problem.

07. PROBLEM – P100107

Find moment of inertia about the centroidal $XX$ and $YY$ axis of the angle section as shown in figure.

MOMENT OF INERTIA OF ANGLE SECTION — PROBLEM FIGURE P100107

Go to solution –

Keywords related to this problem.

08. PROBLEM – P100108

A rectangular hole is made in a triangular section as shown in figure.

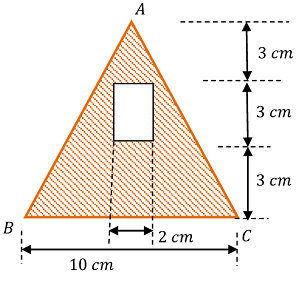
MOMENT OF INERTIA OF A TRIANGULAR SECTION — PROBLEM FIGURE P100108

Determine moment of inertia of the section about $XX$ axis passing through its centre of gravity and through the base $BC$ .

Go to solution –

Keywords related to this problem.

09. PROBLEM – P100109

Figure shows a built up section made of $( 12 \times 4 \ inch )$ channels and $( 12 \ inch \times 3/4 \ inch )$ plates. Find $( I_{xx} )$ and $I_{yy}$ through the centroidal axes, if $I_{yy}$ for channel is $( 12.12 \ inch^4 )$ .

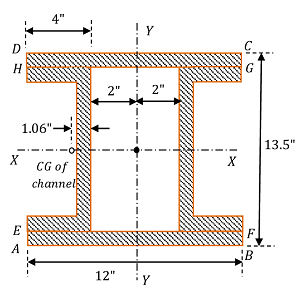
MOMENT OF INERTIA OF JOIST — PROBLEM FIGURE P100109

Area of channel section is $( 9.21 inch^2 )$ . Position of centre of gravity from back of channel is $( 1.06 \ inch )$ and $I_{xx}$ for channel is $( 66.7 \ inch^4 )$ .

Go to solution –

Keywords related to this problem.

10. PROBLEM – P100110

From a right circular cylinder a right cone of the same radius and altitude is cut out as shown in figure. If the radius is $( a )$ and the altitude is $( h )$ , find the moment of inertia of remaining solid about the axis of cylinder.

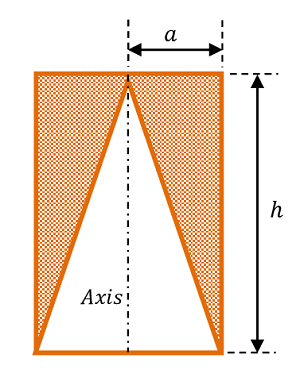
MOMENT OF INERTIA OF A RIGHT CIRCULAR CYLINDER — PROBLEM FIGURE P100110

Go to solution –

Keywords related to this problem.

11. PROBLEM – P100111

Four particles of masses of $( 4 \ kg ), \ ( 2 \ kg ), \ ( 3 \ kg ) \ \& \ ( 5 \ kg )$ are located at the corners $A, \ B, \ C \ \& \ D$ respectively of a square $ABCD$ as shown in figure.

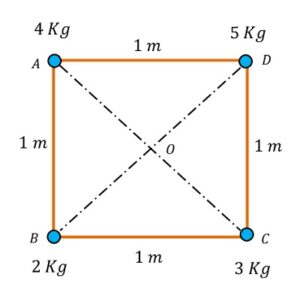
CENTRE OF GRAVITY OF FOUR MASSES — PROBLEM FIGURE P100111

Calculate the moment of inertia of the system about (1) an axis passing through the point of intersection of the diagonals and perpendicular to the plane of the square (2) the side $AB$ and (3) the diagonal $BD$ .

Go to solution –

Keywords related to this problem.

12. PROBLEM – P100112

A cantilever beam $AB$ of length $( l )$ is carrying a point load $( W )$ at its free end $B$ . Find and draw the shear force and bending moment diagram for the beam at important points.

Go to solution –

Keywords related to this problem.

13. PROBLEM – P100113

A cantilever beam $AB$ of length $( l )$ is carrying a uniformly distributed load of $( w )$ per unit length at its full length from $A$ to $B$ .

Find and draw the values of shear force and bending moment at important points and draw the diagram for the beam.

Go to solution –

Keywords related to this numerical problems.

14. PROBLEM – P100114

An overhang beam $AE$ of total length $( 15 \ m )$ is carrying a uniformly distributed load of $( 1000 \ kg / m )$ for $( 5 \ m )$ from end $A$ and $( 1600 \ kg / m )$ for $( 2.5 \ m )$ length from end $E$ . The beam is carrying two point loads of $( 8000 \ kg )$ and $( 4000 \ kg )$ at points $C \ \& \ D$ as shown in figure.

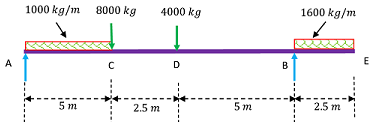
SHEAR FORCE AND BENDING MOMENT DIAGRAM OF A OVERHANG BEAM — PROBLEM FIGURE P100114

Draw the shear force and bending moment diagram for the beam. Also find the maximum bending moment acting any point of the beam.

Go to solution –

Keywords related to this numerical problems.

15. PROBLEM – P100115

An simply supported beam $AB$ of total length $( 5 \ m )$ is carrying a uniformly distributed load of $( 1000 \ N / m )$ for $( 2 \ m )$ from end $A$ and a clockwise couple of $( 1500 \ N \ m )$ at $( 2.5 \ m )$ from end $B$ .

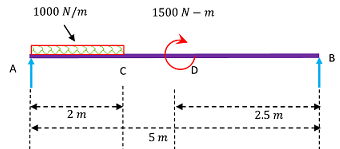
SHEAR FORCE AND BENDING MOMENT DIAGRAM OF A COUPLE LOADED BEAM — PROBLEM FIGURE P100115

Draw the shear force and bending moment diagram for the beam. Also find the maximum bending moment acting any point of the beam.

Go to solution –

Keywords related to this numerical problems.

16. PROBLEM – P100116

An $( I )$ section beam is subjected to a bending moment of $( 500 \ kg \ m )$ at its neutral axis. Section is shown in figure below.

MAXIMUM BENDING STRESS IN A I SECTION BEAM — PROBLEM FIGURE P100116

Find the maximum stress induced in beam.

Go to solution

Keywords related to this numerical problems.

17. PROBLEM – P100117

A timber beam of $( 100 \ mm )$ wide and $( 200 \ mm )$ depth is strengthen by a steel plate of $( 100 \ mm )$ wide and $( 10 \ mm )$ thick screwed at bottom surface of timber beam.

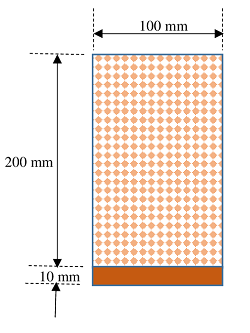
BENDING STRESS IN A FLITCHED BEAM SECTION — PROBLEM FIGURE P100117

Find the moment of resistance of section if allowable stresses in timber and steel are $( 10 \ N / mm^2 )$ and $( 150 \ N / mm^2 )$ respectively. Take $( E_s = 20 E_t )$

Go to solution –

Keywords related to this problem.

18. PROBLEM – P100118

A simply supported beam $( AB )$ of span $( 10 \ m )$ is carrying a point load of $( 10 \ kN )$ at a distance of $( 6 \ m )$ from left end support $A$ . Find out maximum deflection and slope of beam if $( E = 200 \ GN / m^2 )$ and $( I = 1000 \times 10^6 \ mm^4 )$

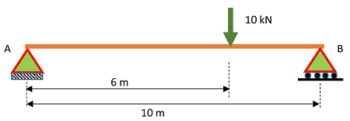
SLOPE AND DEFLECTION IN A POINT LOADED SIMPLY SUPPORTED BEAM — PROBLEM FIGURE P100118

Go to solution –

Keywords related to this problem.

19. PROBLEM – P100119

A cantilever $( 100 \ mm )$ wide and $( 200 \ mm )$ deep projects $( 2 \ m )$ from a wall. The cantilever carries a uniformly distributed load $( 2 \ kN / m )$ over a length of $( 1 \ m )$ from free end and a point load of $( 1 \ kN )$ at free end as shown in figure.

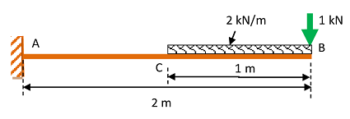
SLOPE AND DEFLECTION IN A UNIFORMLY DISTRIBUTED LOAD CARRYING CANTILEVER — PROBLEM FIGURE P100119

Find the slope and deflection at free end.

Go to solution –

Keywords related to this problem.

20. PROBLEM – P100120

A simply supported beam $AB$ of span $( 4 \ m )$ is loaded with uniformly distributed load of $( 2 \ kN / m )$ as shown in figure.

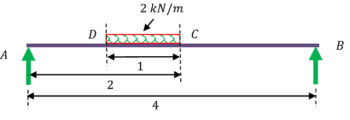
SLOPE AND DEFLECTION IN A UNIFORMLY DISTRIBUTED PART LOAD CARRYING SIMPLY SUPPORTED BEAM — PROBLEM FIGURE P100120

Determine deflection at $C$ and slope at $B$ by moment area method. Take $( EI = 12 \times 10^5 )$

Go to solution –

Keywords related to this problem.

21. PROBLEM – P100121

A beam $ABCD$ is simply supported beam supported at its ends $A$ and $D$ over a span of $( 30 \ m )$ . It is made up of $3$ portions $AB, \ BC \ \& \ CD$ each of $( 10 \ m )$ in length. The moment of inertia of section over each of these individual portions is uniform and moment of inertia $( I )$ values for them are $( I ), \ ( 3I ) \ \& \ ( 2I )$ respectively, where $( I = 2 \times 10^6 cm^4 )$ . Beam carries a point load of $( 15 )$ tonnes at $B$ and another load of $( 30 )$ tonnes at $C$ as shown in figure.

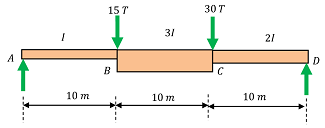
FINDING SLOPE AND DEFLECTION OF A SIMPLY SUPPORTED BEAM BY CONJUGATE BEAM METHOD — PROBLEM FIGURE P100121

Neglecting self weight of beam, calculate the deflection at $B$ and slope at $C$ . Take the values of $( E )$ , the modulus of material of beam $( E = 2 \times 10^6 kg/cm^2 )$ uniform throughout the length.