Centre of Mass of a Solid Cone
A solid cone may be considered to be constructed of numerous tiny particles. These tiny particles have their own masses. Hence, the total mass of the cone is equal to the sum of all tiny masses by which the cone is made up of.
By gravitational nature of earth, each of these tiny particles is attracted towards the centre of the earth with a gravitational force, which is proportional to its mass. This is called weight of particles.
Weight of each tiny particle acts towards the centre of the earth. Therefore, these tiny weights form a system of parallel forces whose direction is towards the centre of earth. The centre of these parallel forces is called the centre of mass of solid cone body.
Centre of mass of a right circular solid cone is determined by integration method.
How to find Centre of Mass of Solid Cone from vertex
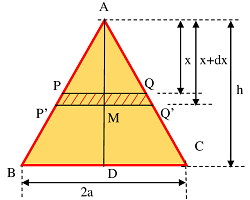
Consider about a right circular solid cone as shown in figure. For convenience, first we will find the centrre of mass of cone from its vertex.
STEP – 1
Let, height of the cone is ( AD = h ) and size of base of cone is ( BC = 2a ) .
Cone is symmetrical about vertical axis ( AD ) . Hence, ( \bar {x} ) co-ordinate of centre of mass will lie on line ( AD ) .
STEP – 2
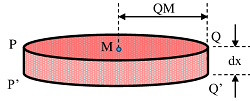
Two cutting planes PQ and P'Q' , separated by a distance ( dx ) and parallel to the base BC are used to cut an element circular disc PP'Q'Q from the cone. Let, the plane PQ is at a distance ( x ) from the vertex A of the cone.
- Therefore, thickness of the cut out circular element PP'Q'Q will be ( dx ) .
- Let, the centre of the cut out element is at M and its radius is ( r )
STEP – 3
From geometry of figure, ( \triangle APM ) and ( \triangle ABD ) are similar triangles.
Hence, from properties of similar triangles, we have –
\left ( \frac {AM}{PM} \right ) = \left ( \frac {AD}{BD} \right )
So, \quad \left ( \frac {x}{r} \right ) = \left ( \frac {h}{a} \right )
Or, \quad r = \left ( \frac {ax}{h} \right )
Let, ( \rho ) is the density of cone material. Then –
Then, \quad \text {Mass of element} = \text {Volume} \times \text {Density} = \text {Area} \times \text {Thickness} \times \text {Density}
Or, \quad dm = ( \pi \ r^2 ) \ ( dx ) \ ( \rho ) = \pi \left ( \frac {a^2}{h^2} \right ) \ x^2 \ \rho \ dx
Therefore, moment of this element about vertex A , will be –
dM = \pi \left ( \frac {a^2 x^2}{h^2} \right ) \rho \ x \ dx = \pi \left ( \frac {a^2}{h^2} \right ) x^3 \rho \ dx
The centre of mass of element will lie at its geometrical centroid at M .
STEP – 4
In similar manner, if cone is cut into more number of elementary circular discs taking the cutting planes at different distances from vertex A then, centre of mass of all such cut out elements will lie along the axis AD .
Here, distance ( x ) for cutting planes is varying from a value \left ( x = 0 \right ) to \left ( x = h \right )
STEP – 5
By applying integration, distance of centre of mass of whole cone from vertex A , is determine as follows.
From definition of centre of mass –
\bar {y} = \frac {\text {Moment of all elementary masses about point A}}{\text {Total mass}}
= \left [ \frac {\sum_{0}^{h} dM }{\sum_{0}^{h} dm} \right ]
= \left [ \sum_{0}^{h} \pi \left ( \frac {a^2}{h^2} \right ) x^3 \rho \ dx \right ] \div \left [ \sum_{0}^{h} \pi \left ( \frac {a^2}{h^2} \right ) \ x^2 \ \rho \ dx \right ]
= \left [ \int\limits_{0}^{h} x^3 \ dx \right ] \div \left [ \int\limits_{0}^{h} x^2 \ dx \right ]
= \left [ \left ( \frac {h^4}{4} \right ) \div \left ( \frac {h^3}{3} \right ) \right ]
= \left ( \frac {3h}{4} \right )
Therefore, centre of mass of solid cone from vertex A is at a distance of \left ( \frac {3h}{4} \right )
Centre of Mass of Solid Cone from base
Since, centre of mass of solid cone from vertex A is at a distance of \left ( \frac {3h}{4} \right )
Therefore, distance of centre of mass of solid cone from base BC will be \left ( \frac {h}{4} \right )
For a right circular solid cone, centre of mass lies at a height of \left ( \frac {h}{4} \right ) from its base.
Centre of Mass of a Hollow Cone
Centre of mass of hollow circular cone is determined by integration method.
Consider about a right circular solid cone as shown in figure. For convenience, first we will find the centrre of mass of cone from its vertex.
Centre of Mass from vertex
STEP – 1
Consider about a hollow right circular cone as shown in figure. Let, height of the cone is ( AD = h ) and size of base of cone is ( BC = 2a ) .
Cone is symmetrical about vertical axis ( AD ) . Hence, ( \bar {x} ) co-ordinate of centre of mass will lie on line ( AD ) .
STEP – 2
Two cutting planes PQ and P'Q' , separated by a distance ( dx ) and parallel to the base BC are used to cut an element circular disc PP'Q'Q from the cone. Let, the plane PQ is at a distance ( x ) from the vertex A of the cone.
- Therefore, width of the cut out circular element PP'Q'Q will be ( dx ) .
- Let, the centre of the cut out element is at M and its radius is ( r )
STEP – 3
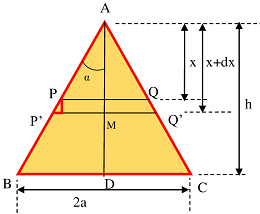
Let, centre of the cut out elementary ring is at M and its radius is ( r ) .
From geometry of cone, we get –
r = \left ( \frac {ax}{h} \right ) .
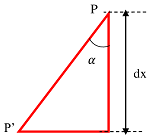
An enlarged view of edge of elementary ring is shown in figure.
Let, vertex angle of the cone is ( 2 \alpha ) .
Therefore, \quad \cos \alpha = \left ( \frac {dx}{PP'} \right )
Or, \quad PP' = dx \ \sec \alpha
Let, ( \sigma ) is the mass per unit area of cone material.
Then mass of elementary ring will be –
\text {Mass} = \text {Area of element} \times \text {Mass per unit area}
= \text {Circumference of element} \times \text {width} \times \text {Mass per unit area}
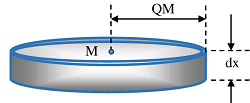
Therefore, \quad dm = ( 2 \pi r ) \times ( PP' ) \ \sigma = 2 \pi \left ( \frac {ax}{h} \right ) ( dx \ \sec \alpha ) \ \sigma
Moment of this elementary mass about vertex A will be –
dM = 2 \pi \left ( \frac {ax}{h} \right ) \ ( dx \ \sec \alpha ) \ x \ \sigma
STEP – 4 & 5
By definition, the distance of centre of mass of cone from vertex A will be –
\bar {y} = \frac {\text {Moment of all elementary masses about point A}}{\text {Total mass}}
= \left [ \frac {\sum_{0}^{h} dM }{\sum_{0}^{h} dm} \right ]
= \left [ \sum_{0}^{h} 2 \pi \left ( \frac {ax}{h} \right ) \ ( dx \ \sec \alpha ) \ x \ \sigma \right ] \div \left [ \sum_{0}^{h} 2 \pi \left ( \frac {ax}{h} \right ) \ ( dx \ \sec \alpha ) \ \sigma \right ]
= \left [ \int\limits_{0}^{h} x^2 \ dx \right ] \div \left [ \int\limits_{0}^{h} x \ dx \right ]
= \left [ \left ( \frac {h^3}{3} \right ) \div \left ( \frac {h^2}{2} \right ) \right ]
= \left ( \frac {2h}{3} \right )
Centre of Mass from base
Therefore, centre of mass from base BC of cone will be –
\bar {y_{base}} = \left [ h - \left ( \frac {2h}{3} \right ) \right ]
= \left ( \frac {h}{3} \right )
A right circular hollow cone has centre of mass at a height of \left ( \frac {h}{3} \right ) from its base.
Centre of Mass of Irregular Lamina
Centre of mass of irregular shaped solid laminar body is determined by vector addition of the position vectors for all tiny mass particles of that body.
Consider about a irregular lamina as shown in figure.
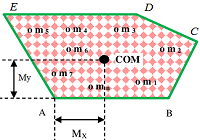
Assume that the lamina is made up of ( n ) numbers of tiny particles of masses ( m_1 ), \ ( m_2 ), \ ....... ( m_n ) etc.
Point ( A ) is taken as the reference point to locate the centre of mass of the body.
Let, the co-ordinates of tiny mass particles from reference point ( A ) are –
( x_1, \ y_1 ), \ ( x_2, \ y_2 ), \ ....... ( x_n, \ y_n ) etc.
These co-ordinates represent the position of centre of mass of individual tiny particles with respect to point ( A ) .
By taking vector sum of all the moments of tiny mass particles about point ( A ) , we will get the position of centre of mass for the whole body.
Therefore, x co-ordinate of centre of mass of body will be –
M_x = \left [ \frac {\left ( m_1 x_1 \right ) + \left ( m_2 x_2 \right ) + ....... + \left ( m_n x_n \right )}{\left (m_1 + m_2 + ..... + m_n \right )} \right ]
Similarly, y co-ordinate of centre of mass of body will be –
M_y = \left [ \frac {\left ( m_1 y_1 \right ) + \left ( m_2 y_2 \right ) + ....... + \left ( m_n x_n \right )}{\left (m_1 + m_2 + ..... + m_n \right )} \right ]
Therefore, whole mass of the body can be assumed to be concentrated at a point whose co-ordinate is \left ( M_x, \ M_y \right ) .
