What are Kinematic Equations of Motion?
The equations governing the motions of an object along a straight line path or a curved path are called Kinematic equations.
The kinematic equations are derived from the theories developed by Newton’s Laws of motion. These equations are of four types –
- Equation for velocity after certain time.
- Equation for displacement covered after certain time.
- Equation for velocity at a certain position.
- Equation for displacement in ( n_{th} ) second.
Derivation of Kinematic Equations
Kinematic equations are based on the Newton’s laws of motion. These equations are derived by two methods –
- Analytical method for derivation of Kinematic equations.
- Integration or Calculus method for derivation of Kinematic equations.
Analytical method for Kinematic Equations
Equations for linear motion and circular motion, both are identical. To determine these equations, first know about the following points –
For Linear motion –
Consider about an object moving with uniform acceleration ( \alpha ) along positive direction of X axis as shown in figure.
In the figure, let –
- x_0 is the position of particle at instant ( t = 0 )
- x is the position of particle at instant ( t = t )
- v_0 is the initial velocity of particle at instant ( t = 0 )
- v is the final velocity of particle at instant ( t = t )
- a is the acceleration acting on the particle.
- S is the displacement in time ( t ) second.

For Circular motion –
Consider about an object moving with angular velocity ( \omega ) in anti-clockwise direction in a circular path of radius ( r ) as shown in figure.
In the figure, let –
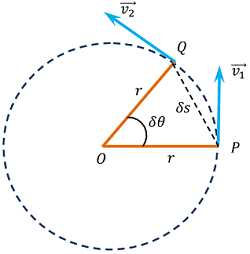
- Initial velocity of particle is ( \omega_0 ) at time ( t = 0 ) .
- Final velocity of particle is ( \omega ) at time ( t = t ) .
- Total angular displacement is ( \theta ) in time ( t ) .
- Angular acceleration acting on the particle is ( \alpha ) .
Now applying Newton’s laws of motion, kinematic equations are derived in following ways –
(1) Velocity after certain time
By definition, linear acceleration of a moving particle is given by –
a = \left ( \frac {\text {Change in velocity}}{\text {Time taken}} \right )
= \left ( \frac {v - v_0}{t - 0} \right )
Or, \quad a t = v - v_0
Or, \quad v = v_0 + a t ………… (1)
This equation gives the final velocity ( v ) of the object after time ( t ) when initial velocity ( v_0 ) is known.
In similar manner, for circular motion, this equation will be –
\omega = \omega_0 + \alpha t ……….. (1a)
(2) Distance covered in certain time
Average velocity of the particle in time interval 0 to t is given by –
v_{av} = \left ( \frac {\text {Displacement}}{\text {Time}} \right ) = \left ( \frac {x - x_0}{t} \right )
Or, \quad ( x - x_0 ) = v_{av} \times t
Or, \quad S = v_{av} \times t
But, \quad v_{av} = \left ( \frac {v_0 + v}{2} \right )
Therefore, \quad S = \left ( \frac {v_0 + v}{2} \right ) \times t
Putting \left [ v = v_0 + a t \right ] from equation (1), we will get –
S = \left [ v_0 t + \left ( \frac {1}{2} \right ) \alpha t^2 \right ]
Therefore, \quad S = v_0 t + \left ( \frac {1}{2} \right ) \ a t^2 ………. (2)
In similar manner, for circular motion this equation will be –
\theta = \omega_0 t + \left ( \frac {1}{2} \right ) \alpha t^2 ……… (2a)
(3) Velocity at a certain position
From equation (1), we have –
v = ( v_0 + a t )
Or, \quad ( v - v_0 ) = a t …………. (3)
Also, \quad \left [ S = v_{av} \times t \right ]
Or, \quad \left ( \frac {v + v_0}{2} \right ) \times t = S
Therefore, \quad ( v + v_0 ) = \left ( \frac {2S}{t} \right ) ………… (4)
Multiplying equations (3) with (4), we will get –
\left ( v + v_0 \right ) \left ( v - v_0 \right ) = \left ( \frac {2 S a t}{t} \right )
Or, \quad ( v^2 - v^2_0 ) = 2 \alpha S
Therefore, \quad v^2 = ( v^2_0 + 2 a S ) ………. (5)
In similar manner, for circular motion this equation will be –
\omega^2 = ( \omega^2_0 + 2 \alpha \theta ) …….… (5a)
(4) Distance covered in ( n_{th} ) second
Distance traveled in ( n_{th} ) second is obtained by the difference of distance traveled in ( n ) seconds and distance traveled in \left ( n - 1 \right ) seconds as shown in figure.
First, distance traveled in first ( n ) seconds is obtained from equation (2), will be –
S_n = v_0 n + \left ( \frac {1}{2} \right ) \ a n^2
And, distance traveled in first \left ( n - 1 \right ) seconds will be –
S_{( n - 1 )} = v_0 ( n - 1 ) + \left ( \frac {1}{2} \right ) \ a ( n - 1 )^2
Hence, distance traveled in ( n_{th} ) second will be –
S_{n_{th}} = S_n - S_{( n - 1 )}
Or, \quad S_{n_{th}} = \left [ v_0 n + \left ( \frac {1}{2} \right ) \ a n^2 \right ] - \left [ v_0 ( n - 1 ) + \left ( \frac {1}{2} \right ) \ a ( n - 1 )^2 \right ]
By simplification, we get –
S_{n_{th}} = v_0 n + \left ( \frac {a}{2} \right ) \left ( 2n - 1 \right ) ……… (6)
In similar manner, for circular motion this equation will be –
\theta_{n_{th}} = \omega_0 + \left ( \frac {\alpha}{2} \right ) \left ( 2n - 1 \right ) ………. (6a)
Integration or Calculus method for Kinematic Equations
Kinematic equations can be evaluated by calculus method as follows –
(1) Velocity after certain time
By definition of linear acceleration, we have –
a = \left ( \frac {dv}{dt} \right )
Or, \quad dv = a dt …….. (1)
Let, when time ( t = 0 ) , initial velocity is ( u )
And when time ( t = t ) , final velocity is ( v )
Integrating equation (1) within the above limits of time and velocity, we will get –
\int\limits_{u}^{v} dv = \int\limits_{0}^{t} a dt
= a \int\limits_{0}^{t} dt
So, \quad \left [ v \right ]_{u}^{v} = a \left [ t \right ]_{0}^{t}
Or, \quad ( v - u ) = a \left ( t - 0 \right )
Therefore, \quad v = ( u + a t ) ………… (2)
(2) Distance covered in a certain time
By definition of Velocity –
\quad v = \left ( \frac {dS}{dt} \right )
Or, \quad dS = v dt = ( u + a t ) dt ……. (3)
When time ( t = 0 ) , distance traveled is ( 0 )
When time ( t = t ) , distance traveled is ( S )
Integrating equation (3) within above limits of time and distance, we get –
\int\limits_{0}^{S} dS = \int\limits_{0}^{t} \left ( u + a t \right ) dt
Or, \quad \int\limits_{0}^{S} dS = u \int\limits_{0}^{t} + a \int\limits_{0}^{t} t dt
Or, \quad \left [ S \right ]_{0}^{S} = u \left [ t \right ]_{0}^{t} + a \left [ \frac {t^2}{2} \right ]_{0}^{t}
Or, \quad ( S - 0 ) = u ( t - 0 ) + a \left [ \frac {t^2}{2} - 0 \right ]
Therefore, \quad S = \left [ u t + \left ( \frac {1}{2} \right ) a t^2 \right ] ……. (4)
(3) Velocity at a certain position
By definition of acceleration and velocity, we have –
a = \left ( \frac {dv}{dt} \right )
= \left ( \frac {dv}{dS} \right ) \times \left ( \frac {dS}{dt} \right )
= \left ( \frac {dv}{dS} \right ) v
Or, \quad a \ dS = v \ dv ………. (5)
When time ( t = 0 ) , initial velocity is ( u ) and distance traveled is ( 0 )
When time ( t = t ) , final velocity is ( v ) and distance traveled is ( S )
Integrating equation (5) within above limits of velocity and distance, we will get –
\int\limits_{0}^{S} \alpha dS = \int\limits_{u}^{v} v dv
Or, \quad a \int\limits_{0}^{S} dS = \int\limits_{u}^{v} v dv
Or, \quad a [ S ]_{0}^{S} = \left [ \frac {v^2}{2} \right ]_{u}^{v}
Or, \quad a \left [ S - 0 \right ] = \left ( \frac {v^2}{2} - \frac {u^2}{2} \right )
Or, \quad 2 a S = ( v^2 - u^2 )
Therefore, \quad v^2 = ( u^2 + 2 a S ) …..…… (6)
(4) Distance covered in ( n_{th} ) second
By definition of velocity, we have –
v = \left ( \frac {dS}{dt} \right )
Or, \quad dS = v dt = ( u + a t ) dt …….. (7)
When time [ t = ( n - 1 ) ] , distance traveled is [ S_{(n - 1)} ]
When time ( t = n ) , distance traveled is ( S_{n} )
Integrating equation (7) within the limits of time and distance, we get –
\int\limits_{S_{(n-1)}}^{S_n} dS = \int\limits_{n}^{(n - 1)} ( u + a t ) dt
Or, \quad [ S ]_{S_{(n-1)}}^{S_n} = u [ t ]_{n}^{(n - 1)} + a \left [ \frac {t^2}{2} \right ]_{n}^{(n - 1)}
Or, \quad S_n - S_{(n - 1)} = u [ n - ( n - 1 ) ] + \frac {a}{2} [ n^2 - ( n - 1 )^2 ]
Or, \quad S_n - S_{(n - 1)} = u + \frac {a}{2} [ n^2 - ( n^2 - 2n + 1 ) ]
Therefore, \quad S_{n_{th}} = u + \frac {a}{2} ( 2n - 1 ) …….. (8)
See numerical problems based on this article.
