What is called Centripetal Acceleration?
Uniform circular motion is an accelerated motion. When a particle is in uniform circular motion, its speed remains constant but its velocity changes continuously due to the change in direction of motion. Hence, a circular motion is accelerated.
A body undergoing uniform circular motion is acted upon by an acceleration which is directed along the radius towards the centre of the circular path. This acceleration is called centripetal acceleration.
Magnitude of Centripetal Acceleration
Consider about a particle moving with a constant speed ( v ) in a circular path of radius ( r ) as shown in figure.
Suppose at time ( t ) the particle is at P and at time ( t + \delta t ) it is at Q . Let, ( v_1 ) and ( v_2 ) are the tangential velocities at points P and Q respectively.
Now, a velocity vector triangle is drawn as shown in figure. In vector triangle –
- Side AB represents velocity vector ( v_2 )
- Side BC represents velocity vector ( - v_1 ) .
Vector AC is now drawn to close the triangle. Then AC will represent the change in velocity [ \Delta v = ( v_2 - v_1 ) ] .
If ( \delta t ) is too small then, ( \text {chord} \ PQ \ \simeq \ \text {Arc} \ PQ . Then, sector OPQ can be considered as a triangle.
Now, in triangles \triangle {OPQ} and \triangle {ABC} , we have –
- \angle POQ = \angle ABC = \delta \theta
- \left ( \frac {OP}{OQ} \right ) = 1 ( each is equal to radius of circle r )
- \left ( \frac {AB}{BC} \right ) = 1 ( each is equal to linear velocity \omega r
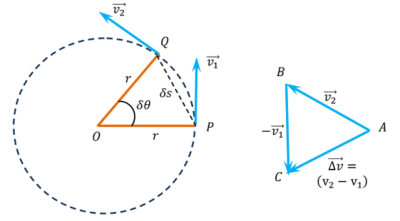
Hence, ( \triangle {OPQ} ) \ \text {and} \ ( \triangle {ABC} ) are congruent ( By SAS ).
Therefore, \quad \left ( \frac {\Delta v}{\delta s} \right ) = \left ( \frac {v}{r} \right )
Or, \quad \Delta v = \left ( \frac {v}{r} \right ) \delta s
Dividing both sides by ( \Delta t ) , we will get –
\left ( \frac {\delta v}{\delta t} \right ) = \left ( \frac {v}{r} \right ) \left ( \frac {\delta s}{\delta t} \right )
In limiting conditions \quad \left ( \frac {dv}{dt} \right ) = \left ( \frac {v}{r} \right ) \left ( \frac {ds}{dt} \right )
But, \quad \left ( \frac {dv}{dt} \right ) = a \quad and \quad \left ( \frac {ds}{dt} \right ) = v
Therefore, \quad a = \left ( \frac {v}{r} \right ) v
Or, \quad a = \left ( \frac {v^2}{r} \right ) = \omega^2 r \quad
Because, \quad ( v = \omega r )
Therefore, magnitude of centripetal acceleration is given by –
a = \left ( \frac {v^2}{r} \right ) \quad Or, \quad a = \omega^2 r
Direction of centripetal acceleration
Centripetal acceleration comes to action when a particle moves in curve or circular path. Uniform circular motion is an accelerated motion. It is the acceleration which keeps necessary force on the body to move in a circular path.
Hence, centripetal acceleration always acts radially to the path of motion and its direction is towards the centre of curve or circular path.
EXAMPLE –
Consider about the figure shown above. When the particle is at point ( P ) , the centripetal acceleration is acting in a direction from point ( P \rightarrow O ) and when the particle is at point ( Q ) , the centripetal acceleration is acting from point ( Q \rightarrow O ) .
Centripetal Force
Centripetal force is the force required to make a body to move along a circular path with a uniform speed. It always acts along the radius and towards the centre of circular path.
According to Newton’s second law of motion, the centripetal force required to move a body of mass ( m ) along a circular path of radius ( r ) is given by –
\text {Force} = \text {Mass} \ \times \ \text {Acceleration}
So, \quad F = m \times \left ( \frac {v^2}{r} \right ) = \left ( \frac {mv^2}{r} \right )
= \left [ \frac {m \left (r \omega \right )^2}{r} \right ] = m r \omega^2
Examples of centripetal forces are –
- When a stone is rotated in a circle, the tension in the string provides the centripetal force.
- For motion of planets around the sun, centripetal force for such motion is provided by gravitational force exerted by sun on the planet.
- When a car is taking a circular turn on a horizontal road, the centripetal force is provided by the force of friction between the tyres and the road.
- Electrostatic force between electron and nucleus provide necessary centripetal force for electrons to move around the nucleus.
See the numerical problems based on this article –
