Moment of Force

What is Moment of a Force?

If a body is free to move and a force is applied on that body, then the effect of this force will produce some action or movement in the body. The effect of force produces either turning tendency or translating tendency in the body. This is due to the effect of moment of a force.

Therefore, moment of a force at a point under consideration, is defined as the product of the magnitude of the force and perpendicular distance of line of action of force from that point under consideration.

The turning or translating tendency of the body depends upon the relative positions of following two points of the body –

The point through which the line of action of force passes.
Hinge point of body or centre of mass of the body.

TO BE NOTED –

If translating motion of a body is arrested by hinging the body at some point, then body will show only turning tendency about the hinge point. This turning effect produced by the force is called, moment of force.

Action of a Moment

To understand the action of a moment, consider about a block kept on a surface. Initially the block is at rest due to its mass inertia.

Now, let a force $( P )$ is applied at some point on block. Due to action of this force, the block will have a tendency to move. This movement of block will depend upon the point of application of force. The trajectory of point of application of the force is called the line of action of force.

The line of action of force may pass through the center of mass or through any other point. Therefore, according to the position of line of action of force, a moment can have two effect – (1) Translation effect of moment and (2) Rotational effect of moment.

Moment producing Translation effect

For a body which is free to move, the centre of mass acts as a pivot point. Depending upon the line of action of force, a free body will have tendency to move either in translation motion or in rotation.

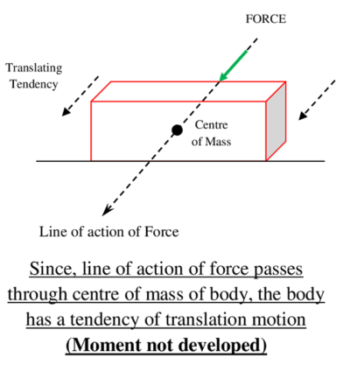
If the line of action of applied force passes through centre of mass, then moment of force will not develop and translation motion will occur. This is illustrated in figure.

Moment producing Rotation effect

If the line of action of force doesn’t passes through the center of mass of the body, a moment will develop that will cause a rotation motion. This is illustrated in figure.

020602 ROTATION EFFECT DUE TO MOMENT OF FORCE

Thus, we get the following conclusions –

Moment of a force is an agent which produces a turning effect or rotating effect on a body.
Position of line of action of force is the main cause which results in generation of a moment and the type of movement of a body.

Magnitude of Moment

Magnitude of moment of a force at a point, is determined by the turning effect produced by the force at that point.

Consider about the body as shown in figure.

Let $( P )$ is the magnitude of the applied force.
The perpendicular distance of line of action of force from center of mass of body is $( d )$ .

Then, product of force $( P )$ and its perpendicular distance $( d )$ will give the magnitude of moment. Therefore, moment of force about center of mass of body will be $( P \times d )$

Distance $( d )$ is called arm of moment.

Therefore, $\quad \text {Magnitude of moment} = \text {Force} \times \text {Perpendicular distance} = \text {Force} \times \text {Arm of moment}$

See numerical problems based on this article.

Direction of a Moment

If moment at a point has a tendency to rotate the point of application in clockwise direction, it is called a clockwise moment. A clockwise moment is taken as a positive quantity in computation of forces.

Similarly, if moment at a point has a tendency to rotate the point of application in anti-clockwise direction, it is called an anti-clockwise moment. An anti clockwise moment is taken as negative quantity in computation of forces.

Couple

A couple is a special case of moment of a force which produces a pure rotation effect.

Consider about a rod $AB$ of length $( d )$ . It is subjected to a pair of equal but opposite direction forces $( P_a )$ and $( P_b )$ acting at its two ends $A$ and $B$ .

Since, the rod is subjected to two forces separated by a distance $( d )$ , each of force will produce its own moment. The forces are acting perpendicular to the axis of rod therefore distance between line of action of forces will be equal to the length of rod.

Each force is producing its own moment. Therefore, rod will be acted upon by two equal moments.
Force $( P_a )$ acting upward at end $A$ will produce a clockwise moment and tend to rotate the rod in clockwise direction whereas, the force $( P_b )$ acting downward at end $B$ will also produce a clockwise moment and tend to rotate the rod in clockwise direction.

This type of action of forces is called a couple.

Two forces acting in a couple are of following nature –

Line of action of two forces are parallel to each other.
The two forces are equal in magnitude but opposite in direction.
Two forces simultaneously act through different lines of action on same body.
They produce a pure rotation of body. There is no translation motion.

Magnitude of Couple

Consider about the rod shown in figure.

$( P_a )$ and $( P_b )$ are the magnitudes of the applied force at the ends $A$ and $B$ respectively.
These forces are acting on the rod such that, the perpendicular distance between their line of actions is $( d )$ .

Then, product of magnitude of one of force $( P_a )$ or $( P_b )$ and perpendicular distance $( d )$ between their line of actions gives the magnitude of couple. Therefore, magnitude of couple will be –

$( P_a \times d )$ or $( P_b \times d )$ .

The distance $( d )$ is called arm of couple.

Therefore, $\quad \text {Magnitude of couple} = \text {Magnitude of any one force} \times \text {Perpendicular distance} = \text {Magnitude of any one force} \times \text {Arm of couple}$

Now consider about a different case as shown in figure.

In this case, forces are parallel to each other but they are not acting perpendicular to axis of the rod. The perpendicular distance between lines of action of forces is shown in figure.

Therefore, Magnitude of a couple is $( P_a \times d )$ or $( P_b \times d )$

See numerical problem based on this article.

P020105

Difference between a Moment & a Couple

We have learnt that, turning effect produced by a force is either a moment or a couple. Most frequently these two terms are used in place of other and seem to be similar. But these have following basic differences between them.

A moment is associated with a single force but a couple is associated with a pair of forces of equal in magnitude, opposite in direction which are acting on same body.
A moment can produce a translating or turning tendency but a couple always produces only turning tendency.