What is Electromotive Force?
Electromotive force of a source of electric current supply is defined as the potential difference between the terminals of the cell in open circuit i.e. when no current is drawn from the cell.
- In short form electromotive force is written as emf.
- Electromotive force is not a force, rather it is the work done by a cell to bring a unit positive charge from one terminal to the other terminal of the cell.
- In short form, electromotive force is written as EMF.
EMF of a cell doesn’t depends upon –
- Size of the electrodes of the cell.
- Distance between the electrodes of cell.
- Quantity of electrolyte used in the cell.
Terminal Potential Difference
Terminal potential difference of a cell is defined as the potential difference between the terminals of the cell when it is connected to a closed circuit i.e. when current is being drawn from the cell by circuit.
Cell
A cell is defined as a device which provides source of electric supply and uses chemical energy to convert it into electrical energy. It is also called a source of electromotive force.
- A cell has two terminals by which the external circuit is connected.
- The positive terminal is called anode and negative terminal is called a cathode.
- When a conductor is connected between these terminals, cell drives an electric current through it.
To get higher electromotive force or current in the circuit, many cells are collectively used in series or in parallel or in mixed combination. A combination of such cells is called a battery.
Internal Resistance
Internal resistance of a cell is defined as the opposition offered by the electrolyte and electrodes of a cell to the flow of electric current through it.
Consider a cell of e.m.f ( E ) and internal resistance ( r ) is connected to a circuit having external resistance ( R ) as shown in figure.
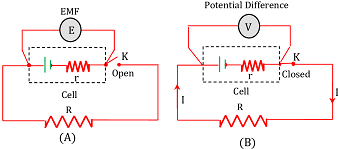
- When the key ( K ) is open no current is drawn from the cell. So, the voltmeter reads the value of EMF of the cell.
- When the key ( K ) is closed current is drawn from the cell in the circuit. So, the voltmeter will read potential difference of the cell.
Since, ( R ) and ( r ) are connected in series, therefore current through the circuit will be –
I = \left ( \frac { E }{ R + r } \right )
Or, \quad E = ( IR + Ir ) ………. (1)
Since external resistor ( R ) is also connected in parallel to the electrodes of the cell, so the terminal potential difference is the potential difference across the resistor ( R ) .
Therefore, \quad V = IR …….. (2)
Hence, equation (1) becomes –
E = V + Ir
Or, \quad V = E - Ir ……… (3)
This shows that terminal potential difference is less than the EMF of the cell.
Hence, now the voltmeter reads the value of terminal potential difference ( V ) of the cell which is less than initial reading of EMF ( E ) .
Electromotive Force & Potential Difference
| Sl. No. | Electromotive Force. | Potential Difference. |
| 1 | It is a measurable quantity when the circuit is open. | It is a measurable quantity when the circuit is closed. |
| 2 | Electromotive force is independent of any external resistance in the circuit. | Potential difference between two points in a circuit is proportional to the resistance between these points. |
| 3 | Electromotive force is greater than potential difference between two terminals of the cell. | Potential difference between two terminals of the cell is less than electromotive force. |
| 4 | Electromotive force is a term which is related to the source of supply of electric current. | Potential difference is a general term which indicates the effect of electric current in circuit. |
| 5 | Variation of electromotive force ( E ) with external resistance ( R ) is shown in figure (A). From graph it can be concluded that ( E ) is independent of external resistance ( R ) . | Variation of potential difference ( V ) with external resistance ( R ) is shown in figure (B). From graph it can be concluded that ( V ) is directly proportional to external resistance ( R ) . |
Following figures shows the effect of external resistance on EMF and potential difference of a cell.
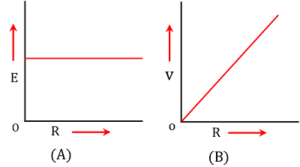
Figure (A) shows effect of external resistance on EMF of a cell and figure (B) shows effect of external resistance on terminal potential difference.
Charging of a Cell or Battery
Consider that a cell or battery of EMF ( E ) and internal resistance ( r ) is being charged by a charger.
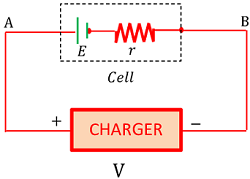
The charging voltage ( V ) is kept equal to or more than EMF ( E ) of the cell which is under charging.
Therefore, net potential difference across the cell will be ( V - E )
This net potential difference is equal to the voltage drop inside the cell.
Therefore, \quad ( V - E ) = Ir
Or, \quad V = ( E + Ir )
Therefore, charging voltage must be kept greater than the EMF of cell being charged at least by an amount ( Ir ) where ( I ) is the charging current and ( r ) is the internal resistance of the cell.
