What is Ohm’s law of electric current?
It states that –
The current flowing through a conductor is directly proportional to the applied potential difference across the ends of the conductor if other physical conditions such as temperature, pressure, strain etc. remain unchanged.
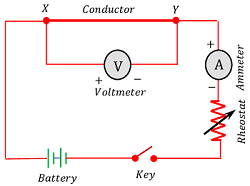
Consider that, ( I ) is current flowing through a conductor when a potential difference ( V ) is applied across the ends of conductor.
Then, by Ohm’s law –
I \propto V
Or, \quad V \propto I
- Therefore, \quad V = IR
Or, \quad \left ( \frac { V }{ I } \right ) = R
Where ( R ) is the constant of proportionality called electric resistance of conductor.
Ohm’s Law & Electric Resistance
From Ohm’s law, we have –
V \propto I
Or, \quad \left ( \frac { V }{ I } \right ) = \text {Constant} = R
Here, ( R ) is a constant of proportionality called electric resistance of conductor.
Therefore, resistance of a conductor is defined as the ratio of the potential difference across the ends of conductor to the current flowing through the conductor.
Ohm
- Ohm ( Ω ) is the SI unit of electric resistance.
1 \ \text {ohm ( Ω )} = \frac { 1 \ \text {volt ( V )}}{ 1 \ \text {Ampere ( A )}}
Therefore, one ohm is the resistance of a conductor if one ampere of current flows through that conductor when potential difference of one volt is applied across its ends.
See numerical problems based on this article.
Factors affecting Resistance of an element
The value of resistance ( R ) of a conductor depends upon the following factors –
- Nature of material of a conductor.
- Area of cross section of conductor.
- Length of the conductor.
- Temperature of the conductor.
Effect of nature of material
Different conductors at same temperature having same length and same cross sectional area but made of different materials will offer different resistance when applied across the terminals of equal potential differences.
Hence, resistance of a conductor depends upon the material chosen for conductor.
Effect of cross section
Different conductors made of same material and at same temperature having same length but of different cross sectional area, offer different resistances when applied across the terminals of equal potential difference.
Hence, resistance of a conductor depends upon the cross sectional area ( A ) chosen for the conductor.
The resistance of a conductor is inversely proportional to the cross sectional area ( A ) .
Therefore, \quad R \propto \left ( \frac { 1 }{ A } \right ) ………. (1)
Effect of length of conductor
Different conductors made of same material at same temperature having same cross sectional area but of different length will offer different resistance when applied across the terminals of equal potential differences.
Hence, resistance of a conductor depends upon length ( l ) chosen for the conductor.
The resistance of a conductor is directly proportional to the length ( l ) .
Therefore, \quad R \propto l …….. (2)
By combining equations (1) and (2) we get –
R \propto \left ( \frac { l }{ A } \right )
Or, \quad R = \rho \left ( \frac { l }{ A } \right ) …….. (3)
Where, \rho is a constant of proportionality which depends upon the material of the conductor. It is known as specific resistance or resistivity of the material.
Effect of temperature of conductor
Resistance offered by a metallic conductor is due to the collision between free electrons and the ions present in the metallic conductor. When temperature increases the amplitude of vibration of electrons or ions increases and hence the collisions between electrons and ions become more frequent. This leads to the increase in the resistance.
Thus, resistance of a conductor increases or decreases with increase or decrease in temperature.
Resistance of a conductor is directly proportional to the –
- Resistance of conductor at ( 0 \degree C )
- Increase in temperature.
Therefore, the relation between resistance and temperature of a conductor is given by –
R = R_0 \left ( 1 + \alpha \Delta \theta \right )
Where –
- ( R_0 ) and ( R ) are the resistances of conductor at ( 0 \degree C ) and ( \theta \degree C ) respectively.
- ( \Delta \theta ) is the raise in temperature of conductor and
- ( \alpha ) is a constant of proportionality called temperature coefficient of resistance.
Temperature coefficient of Resistance
Temperature coefficient of resistance is defined as the rate of change in resistance of a conductor per unit change in temperature per unit original resistance.
It is denoted by ( \alpha )
Therefore, \quad \alpha = \left [ \frac { \left ( R - R_0 \right )}{ R_0 \left ( T - T_0 \right )} \right ]
Or, \quad \alpha = \left [ \frac { \Delta R }{ R_0 \Delta T } \right ]
Temperature coefficient of resistivity ( \alpha ) is different for different materials.
- For good conducting metals, the value of temperature coefficient of resistance ( \alpha ) is positive. Hence the resistance of conductors increases with increase in temperature.
- For insulators and semiconductors, the value of temperature coefficient of resistance ( \alpha ) is negative. Hence the resistance of insulators and semiconductors decreases exponentially with increase in temperature.
Electric energy derivation from Ohm’s Law
Consider an electric circuit element through which a current ( I ) flows from one point to another point (say point A to B ) for time ( t ) . Let ( q ) is the charge flowing between these points in this time interval.
Then, \quad q = I t \quad
Because \quad I = \left ( \frac { q }{ t } \right )
If ( V ) be the terminal potential difference between the points A and B , then work done to carry the charge from point A to B is given by –
W = V q = V I t
This work done is equal to the electrical energy consumed in transferring charges from point A to B .
Therefore, \quad E = V I t = V \left ( \frac { V }{ R } \right ) t
Or, \quad E = \left ( \frac { V^2 }{ R } \right ) t
Also, \quad E = V I t = \left ( I R \right ) I t = I^2 R t
- SI unit of electrical energy is joule.
Electric Power derivation from Ohm’s Law
Electric power is defined as the rate of doing electrical work.
Therefore, Electric power \quad P = \left ( \frac {\text {energy produced}}{\text {time}} \right ) = \left ( \frac { E }{ t } \right )
Or, \quad P = \left ( \frac { E }{ t } \right ) = \left ( \frac { V^2 }{ R t } \right ) t
Or, \quad P = \left ( \frac { V^2 }{ R } \right ) = V \left ( \frac { V }{ R } \right ) = V I
Also, \quad P = \left ( \frac { E }{ t } \right ) = \left ( \frac { I^2 R t }{ t } \right ) = I^2 R
Thus, electric power is defined as the product of applied voltage and current flowing through the circuit.
Watt
SI unit of electric power is watt.
1 \ \text {watt} = 1 \ \text {Ampere} \ \times \ 1 \ \text {Volt}
If one ampere of current flows through a circuit having potential difference across its ends is one volt, the the power of the circuit is called one watt.
See numerical problems based on this article.
