What happens when a charge moves in Electric Field?
When a charge is projected to move in an electric field, it will experiences a force on it.
The projected charge while moving through the region of electric field, gets deflected from its original path of motion. The trajectory of the path of motion is a parabola.
From definition of electric field intensity, we know that –
Force experienced by a moving charge ( q ) in an electric field ( \vec {E} ) is –
\vec {F_e} = q \vec {E}
Direction of this electric force is same as that of the direction of electric field ( \vec {E} ) .
Motion of a charge in an Electric Field
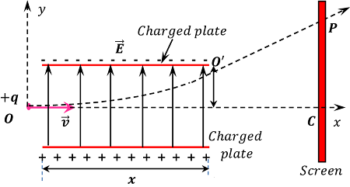
Consider that, an uniform electric field ( \vec {E} ) is set up between two oppositely charged parallel plates as shown in figure.
A proton or any other positively charged particle is projected from point O in the direction normal to the direction of magnetic field and allowed to move further. Let –
- Direction of magnetic field is along Y axis.
- Direction of projection of charged particle is along X axis.
- Magnitude of charge on the particle is (+ q) .
- Mass of the charged particle is ( m ) .
- Velocity of projection is ( \vec {v} )
- Intensity of electric field in the region is ( \vec {E} ) .
From Lorentz law, electric force acting on charge (+ q) due to electric field ( \vec {E} ) will be –
\vec {F} = q \vec {E}
Direction of electric force will be along the direction of ( \vec {E} ) . Hence, the charged particle is deflected in upward direction.
Thus, acceleration produced in the charged particle will be –
\vec {a} = \left ( \frac {\vec {F}}{m} \right )
= \left ( \frac {q \vec {E}}{m} \right )
The magnitude of this acceleration will be –
a = \left ( \frac {qE}{m} \right ) ……… (1)
Direction of acceleration will be in the direction of ( \vec {E} ) .
As soon as the charged particle leaves the region of electric field, it travels in a straight line due to inertia of motion and hits the screen at point P .
Let –
- Length of electric field region is ( x ) along X axis.
- Width of electric field region is ( y ) along Y axis.
- Time taken by the charged particle to travel the region of electric field is ( t ) .
Using kinematic equation of motion, we get the features for motion of the charged particle in electric field region –
S = ut + \frac {1}{2} at^2
1. Horizontal motion of charge in X direction –
For horizontal motion of the particle in X direction –
( S = x ) \quad ( u = v ) \quad \text {and} \quad ( a = 0 ) ( because no force is acting on the particle along X direction )
Hence, \quad x = vt
So, \quad t = \left ( \frac {x}{v} \right ) ………. (2)
2. Vertical motion of charge in Y direction –
For vertical motion of the particle in Y direction –
( S = y ) \quad ( u = 0 ) \quad \text {and} \quad \left ( a = \frac {qE}{m} \right ) ( because initially the particle was moving along X direction ).
y = \left ( \frac {1}{2} \right ) at^2
= \left ( \frac {1}{2} \right ) \left ( \frac {qE}{m} \right ) t^2
From equation (2), substituting the value of ( t ) , we get –
y = \left ( \frac {1}{2} \right ) \left ( \frac {q E}{m} \right ) \left ( \frac {x}{v} \right )^2
= \left ( \frac {q E x^2}{2 m v^2} \right ) ……. (3)
Since, ( q ), \ ( E ), \ ( m ) \ \text {and} \ ( v ) are constants for the charged particle, so \left ( \frac {qE}{2mv^2} \right ) becomes a constant. Let, it is represented as ( K )
Therefore, \quad y = K x^2
Hence, the trajectory of motion of the charged particle in the region of electric field can be represented as –
y \propto x^2 . ( This is the general equation of a parabola. )
Hence, a charged particle moving in a uniform electric field follows a parabolic path as shown in the figure.
Specific Charge
Charge per unit mass of a charged particle is called its specific charge.
\text {Specific charge} = \left ( \frac {\text {Magnitude of charge on charged particle}}{\text {Mass of charged particle}} \right )
If a charged particle has a charge ( q ) and mass ( m ) , then –
q_s = \left ( \frac {q}{m} \right )
For the charge moving in electric field from equation (3), we get –
y = \left ( \frac {q E x^2}{2 m v^2} \right )
By re-arranging the expression, we get –
y = \left ( \frac {1}{2} \right ) \left ( \frac {q}{m} \right ) \left ( \frac {Ex^2}{v^2} \right ) = K' \left ( \frac {q}{m} \right )
= \left ( \frac {1}{2} \right ) ( q_s ) \left ( \frac {Ex^2}{v^2} \right ) = K' \left ( \frac {q}{m} \right )
Therefore, motion of the charged particle in electric field is proportional to its specific charge. Its deflection depends upon the specific charge
y \propto q_s
Thus, if a charged particle has more specific charge, it will deflect more in the electric field.
SPECIAL CASES
- Force on a charged particle acts in the direction of electric field. Hence, when a positive charged particle moves along the direction of electric field its motion gets accelerated along a straight line in same direction.
- While passing through a potential difference ( V ) , energy gain by a charge ( q ) is given by \left [ KE = \left ( \frac {1}{2} \right ) mv^2 = qV \right ] .
- When a charged particle moves at right angle to a uniform electric field, it follows a parabolic path.
See numerical problems based on this article.
