What is the Second Law of Thermodynamics?
The first law of thermodynamics states that, energy can neither be created nor destroyed. The total quantity of energy in the universe remains same. The Second Law of Thermodynamics is telling about the nature of energy. It describes the relationships between thermal energy and other forms of energy.
The second law of thermodynamics tells that –
- Whenever energy is transferred or transformed into another form, some part of it goes wasted.
- There is a natural tendency of any isolated system to degenerate into a more disordered state.
- Entropy of a system always increases.
Second law of thermodynamics can be stated in two different ways, called –
- Kelvin Plank’s statement.
- Clausius statement.
Kelvin-plank Statement
According to Kelvin Plank statement, second law of thermodynamics is stated as –
It is impossible to construct an engine which will produce no effect other than extracting heat from a hot reservoir and converting it into an equivalent amount of work.
This law is applicable for heat engines.
Consider about a heat engine. Let –
- ( Q_1 ) is the heat absorbed from hot reservoir at temperature ( T_1 ) .
- ( Q_2 ) is the heat released to the cold sink at temperature ( T_2 )
- ( W ) is the work done by the engine.
- ( T_2 < T_1 )
Therefore, Kelvin Plank’s statement for second law of thermodynamic tells that –
- A working substance working in a cycle in an engine can’t convert all of the heat extracted from the source into an equivalent amount of work i.e. ( W < Q_1 )
- It must release some quantity of heat to a sink which is at comparatively low temperature i.e. ( Q_2 > 0 ) .
Clausius Statement
According to Clausius statement, second law of thermodynamic stated as –
It is impossible for a machine to work without the help of any external agency which transfer heat extracting from a cold reservoir and releasing it to a sink at higher temperature.
This law is applicable for heat pumps or refrigerators.
Consider about a heat pump. Let –
- ( Q_2 ) is the heat absorbed from cold reservoir at temperature ( T_2 ) .
- ( Q_1 ) is the heat released to the hot sink at temperature ( T_1 )
- ( W ) is the work input to the heat pump.
- ( T_2 < T_1 )
Therefore, Clausius statement for second law of thermodynamic tells that –
- A working substance working by itself in a cycle can’t extract heat from a source at low temperature and release it to a sink at higher temperature.
- Work must be supplied to the machine to work and absorb heat from cold reservoir and deliver it to the hot sink. This work is normally done by an electric compressor. Therefore, work done on machine must be positive i.e. ( W > 0 ) .
Significance of Second Law of Thermodynamics
Based on the statements for second law of thermodynamic it is concluded that –
- Second law of thermodynamic puts a fundamental limit on the working performance of a heat engine or a refrigerator.
- The efficiency of a heat engine can never be 100 \% .
- Maximum efficiency is achieved by a thermodynamic cycle which is a reversible cycle called Carnot cycle.
- The coefficient of performance of a refrigerator can never be infinite.
Heat Engine
Heat engine is a mechanical device which continuously converts heat energy into mechanical energy in a cyclic process.
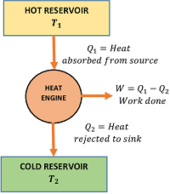
A typical heat engine is represented in figure. It has the following essential parts –
- It is a heat reservoir at higher temperature ( T_1 ) .
- It has infinite thermal capacity such that any amount of heat can be drawn from it and there will be no drop in temperature.
- It is a heat reservoir at a lower temperature ( T_2 ) .
- It has infinite thermal capacity such that any amount of heat can be added to it and there will be no rise in temperature.
- It is a substance which performs mechanical work when heat is supplied to it.
- It can be a solid, a liquid or a gaseous substance.
Example –
- Petrol or diesel is the working substance in an internal combustion engine.
- Freon or Ammonia is the working substance in a refrigerator or air conditioner.
Working principle of Heat Engine
A heat engine works in four steps in every cycle of operation. These are –
- The working substance absorbs heat ( Q_1 ) from the source at temperature ( T_1 ) .
- Then it converts a part of this heat energy into mechanical work ( W ) .
- The remaining amount of heat ( Q_2 ) is then released into the sink at temperature ( T_2 ) .
- The obtained work done ( W ) in each cycle is transferred to the environment by mechanical arrangement to get mechanical energy.
Efficiency of Heat Engine
The efficiency of a heat engine is defined as the ratio of net work done by the engine in one cycle to the amount of heat absorbed by the working substance from the source.
The working substance returns to its initial state after completing each cycle. Hence, there is no change in its internal energy.
By the first law of thermodynamics we have –
\text {Net heat absorbed in a cycle} = \text {Work done}
Or, \quad ( Q_1 - Q_2 ) = W
Therefore, efficiency of heat engine will be –
\eta = \left ( \frac {W}{Q_1} \right ) = \left ( \frac {Q_1 - Q_2}{Q_1} \right )
Or, \quad \eta = \left [ 1 - \left ( \frac {Q_2}{Q_1} \right ) \right ]
Therefore, efficiency of a heat engine is always less than unity.
Heat Pump
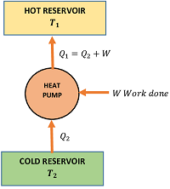
A heat pump or a refrigerator is a reversed Carnot’s heat engine. It works on the principle of Carnot engine working in the reverse direction.
Given figure shows a typical heat pump. It works in a cycle in following steps –
- The working substance absorbs an amount of heat ( Q_2 ) from a cold reservoir at temperature ( T_2 ) .
- An amount of work ( W ) is done on it by an external agency (a prime-mover or an electric motor).
- It rejects a larger quantity of heat ( Q_1 ) to the reservoir at temperature ( T_1 ) .
In domestic refrigerator work is done by an electric motor and refrigerant Freon ( CCl_2F_2 ) is used as a working substance.
Coefficient of Performance
Coefficient of performance of a heat pump or refrigerator is defined as the ratio of amount of heat removed ( Q_2 ) per cycle to the mechanical work ( W ) required to be done on it.
Therefore, \quad \beta = \left ( \frac {Q_2}{W} \right )
But, \quad Q_1 = ( Q_2 + W )
Therefore, \quad \beta = \left ( \frac {Q_2}{Q_1 - Q_2} \right )
Since \quad \left ( \frac {Q_1}{Q_2} \right ) = \left ( \frac {T_1}{T_2} \right )
Therefore, \quad \beta = \left ( \frac {T_2}{T_1 - T_2} \right )
Ideal Thermodynamic Cycle
A Carnot cycle is an ideal reversible heat engine cycle that operates between two temperatures ( T_1 ) and ( T_2 ) .
Carnot Cycle
Carnot cycle operates on ideal gas contained in a piston cylinder arrangement. It consists of 4 thermodynamic processes as shown in figure –
Step -1 Isothermal expansion.
Let, initial state of the gas in the cylinder is ( P_1, \ V_1, \ T_1 ) and final state is ( P_2, \ V_2, \ T_2 ) .
Since, the gas expands in isothermal process so ( T_1 = T_2 )
Let, ( Q_1 ) is heat absorbed from the source and ( W_1 ) is the work done by the gas in the isothermal expansion process. Then –
W_1 = Q_1 = n R T_1 \ln \left ( \frac {V_2}{V_1} \right )
Or, \quad W_1 = Q_1 = n R T_2 \ln \left ( \frac {V_2}{V_1} \right )
= \text {Area ABMKA} .
Step -2 Adiabatic expansion.
The gas is now allowed to expand in adiabatic process so that temperature falls to ( T_3 ) .
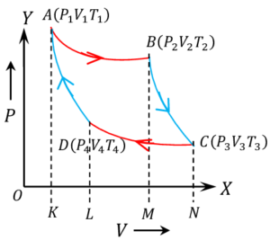
Let, ( W_2 ) work done by the gas in this expansion which takes to final state ( P_3, V_3, T_3 ) . Then –
W_2 = \left [ \frac {nR \left ( T_2 - T_3 \right )}{\gamma - 1} \right ]
= \left [ \frac {nR \left ( T_1 - T_3 \right )}{\gamma - 1} \right ]
Because \quad ( T_1 = T_2 )
So, \quad W_2 = \text {Area BCNMB} .
Step -3 Isothermal compression.
The gas is now allowed to compress in isothermal process from initial condition of ( P_3, \ V_3, \ T_3 ) to final state ( P_4, \ V_4, \ T_4 ) .
Since, the process is isothermal process so ( T_3 = T_4 )
Let, ( Q_2 ) heat is released by the gas to the sink and ( W_3 ) work done on the gas in compressing the gas. Then –
W_3 = Q_2 = n R T_3 \ln \left ( \frac {V_3}{V_4} \right )
= Q_2 = n R T_4 \ln \left ( \frac {V_3}{V_4} \right )
= \text {Area CDLNC} .
Step -4 Adiabatic compression.
The gas is now allowed to compress in adiabatic process so that temperature rises to ( T_1 ) .
Let, ( W_4 ) work done on the gas in this compression which takes to final state ( P_1, V_1, T_1 ) . Then –
W_4 = \left [ \frac {nR \left ( T_1 - T_4 \right )}{\gamma - 1} \right ]
= \left [ \frac {n R \left ( T_1 - T_3 \right )}{\gamma - 1} \right ]
Because, \quad ( T_4 = T_3 )
So, \quad W_4 = \text {Area DAKLD} .
Therefore, net work done = Total work done by the gas in expansion – Total work done to the gas in compression.
Or, \quad W = [ ( W_1 + W_2 ) - ( W_3 + W_4 ) ]
= [ W_1 + W_2 - W_3 - W_4 ]
But, \quad W_2 = W_4
Therefore, \quad W = ( W_1 - W_3 ) = ( Q_1 - Q_2 )
= \text {Area ABCDA}
Hence, work done by a Carnot cycle is numerically equal to the area enclosed by the Carnot cycle.
Carnot Efficiency
Efficiency of Carnot cycle engine is given by –
\eta = \left ( \frac {W}{Q_1} \right ) = \left ( \frac {Q_1 - Q_2}{Q_1} \right )
= \left [ 1 - \left ( \frac {Q_2}{Q_1} \right ) \right ]
But ( Q_1 ) is the heat added at constant temperature ( T_1 = T_2 ) and ( Q_2 ) is the heat rejected at constant temperature ( T_3 = T_4 )
Therefore, \quad \eta = \left [ 1 - \left ( \frac {Q_2}{Q_1} \right ) \right ]
= \left [ 1 - \frac {n R T_3 \ \ln \left ( V_3 / V_4 \right )}{nRT_1 \ \ln \left ( V_2 / V_1 \right )} \right ] ………. (1)
Since, step 2 and 4 are adiabatic processes –
Therefore, \quad T_2 V^{\gamma - 1}_2 = T_3 V^{\gamma - 1}_3 …….. (2)
And, \quad T_1 V^{\gamma - 1}_1 = T_4 V^{\gamma - 1}_4 …….. (3)
Dividing equation (2) by equation (3), we will get –
\left ( \frac {V_2}{V_1} \right )^{\gamma - 1} = \left ( \frac {V_3}{V_4} \right )^{\gamma - 1}
Because \quad ( T_1 = T_2 ) and \quad ( T_3 = T_4 )
Therefore, \quad \left ( \frac {V_2}{V_1} \right ) = \left ( \frac {V_3}{V_4} \right )
Putting this value in expression (1) for efficiency we get –
\eta = \left [ 1 - \left ( \frac {T_3}{T_1} \right ) \right ] ………… (4)
See numerical problems based on this article.
