Resolution of Forces

What is called Resolution of Forces?

In analyzing the force problems, sometimes we require to evaluate the effect of a force in a certain direction of our interest. This is done by resolution of forces in required directions. It is just an opposite process of addition of forces. The forces formed after splitting are called components of forces.

Therefore, resolution is the process of splitting of a force into two or more forces in such a way that, their combined effect is same as that of the given force.

In resolution process, a single unknown force is divided into two component forces in a suitable direction of our interest.
The resolution of a force is just opposite process to the addition of forces.
Resolution of a force means dividing a given force into two components.
It is very helpful in solving analytical numerical problems of complicated force system.
A component of a force in any direction gives a measure of the effect of the given force in that direction.

Component Forces

By resolution of a force, we get two forces in certain direction as per our requirement. The split out forces are called Components of Force.

Therefore, components of a force are the two or more split out forces whose in such a way that, their combined effect is same as that of the given force.

In solving the problems of a system of forces, it is very useful to split a single force into its component forces in desired directions in analytical analysis.

Resolution of a Force into two Components

The process of resolution of a force into two components, is just an opposite process of addition of forces by parallelogram law.

Consider about a force $( \vec R )$ , which is acting along line $OC$ as shown in figure. Suppose that, we have to find the components of this force along the directions $OX$ and $OY$ .

Let, the line of directions $OX$ and $OY$ are making angles $( \alpha )$ and $( \beta )$ respectively with the line of action $OC$ of force $( \vec R )$ .

Line $CA$ is drawn parallel to $OY$ meeting the line $OX$ at point $A$ .
Line $CB$ is drawn parallel to $OX$ meeting the line $OY$ at point $B$ .

Then, $OA$ and $OB$ will represent the components of force $( \vec R )$ along the directions $OX$ and $OY$ respectively.

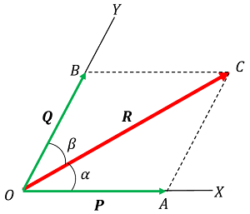
Let, the resolved components are $( OA = \vec P )$ and $( OB = \vec Q )$ as shown in vector diagram.

From geometry of the vector diagram, we have –

$\angle {OCA} = \angle {BOC}$ (Alternate angles).

That means, $\quad \angle {OAC} = \left [ 2 \pi - \left ( \alpha + \beta \right ) \right ]$

Let, $\quad \left ( \alpha + \beta \right ) = \theta$

Therefore, $\quad \angle {OAC} = \left ( 2 \pi - \theta \right )$

By applying sin law in $( \triangle OAC )$ , we will get –

$\left [ \frac { OA }{ \sin \beta } \right ] = \left [ \frac { AC }{ \sin \alpha } \right ] = \left [ \frac { OC }{ \sin ( 2 \pi - \theta ) } \right ]$

By trigonometrical ratios, we know –

$\sin ( 2 \pi - \theta ) = \sin \theta$

Application of Sin Law

By applying Sin Law, we will get –

Therefore, $\left [ \frac { P }{ \sin \beta } \right ] = \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \theta \right ) } \right ]$

$= \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]$

$= \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]$

Also, $\quad \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]$

Therefore, $\quad P = \left [ \frac { R \sin \beta }{ \sin \left ( \alpha + \beta \right )} \right ] \quad$ and $\quad Q = \left [ \frac { R \sin \alpha }{ \sin \left ( \alpha + \beta \right )} \right ]$

Rectangular Components

If we resolve a force in the direction of two mutually perpendicular directions by analytical or graphical methods, the component forces so obtained are called rectangular components.

Let, $OX$ and $OY$ are at right angles to each other as shown in figure.

Since, $( \angle XOY = 90 \degree )$ and $( \angle XOC = \alpha )$

That means $\quad \left [ \beta = \left ( 90 \degree - \alpha \right ) \right ]$

So, $\quad \left ( \frac{ P }{ R } \right ) = \cos \alpha$

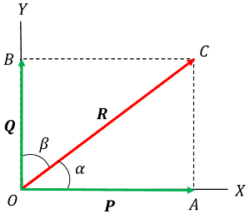
Or, $\quad P = R \cos \alpha$ ……. (1)

And, $\quad \left ( \frac{ Q }{ R } \right ) = \cos \beta = \cos \left ( 90 \degree - \alpha \right )$

By trigonometrical ratios, we have $\cos ( \pi - \alpha ) = \sin \alpha$

Therefore, $\quad \left ( \frac{ Q }{ R } \right ) = \sin \alpha$

Or, $\quad Q = R \sin \alpha$ ……. (2)

When the component forces $( P )$ and $( Q )$ are at right angles to each other, they are called rectangular components of force $( R )$ .

Therefore, from equation (1) and (2) we get –

Resolved component of force $( R )$ in a direction inclined at an angle $( \alpha )$ to $( R )$ is $( P = R \cos \alpha )$
Resolved component of force $( R )$ in a direction inclined at an angle $\left ( \beta )\right )$ to $( R )$ is $( Q = R \cos \beta = R \sin \alpha )$

See numerical problems based on this article.

How to resolve a force in Rectangular Components?

Technique of resolving a force into rectangular components is illustrated below.

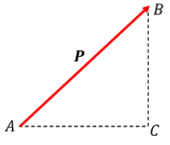
Consider about a force $( P )$ represented by $AB$ as shown in figure. We have to resolve this force into rectangular component forces in directions $AC$ and $CB$ .

While resolving a force following technique is followed –

A right angle triangle $( \triangle ABC )$ is drawn taking the force $( P )$ as hypotenuse as shown in figure.
020403 TECHNIQUE OF RESOLVING A FORCE
Other two sides i.e. base and perpendicular of triangle are drawn represented by $AC$ and $CB$ respectively. These sides will then represent the direction and magnitude of the component forces.
Now applying geometry, one of the known angles of $( \triangle ABC )$ is identified. Let, as per given data in the problem we are able to get the value of angle $( \angle BAC = \alpha )$
The side attached with the known angle i.e. side $AC$ will be considered as base of triangle.
Now apply trigonometry and find the magnitude of component forces in directions $AC$ and $CB$ as follows.