What is called Addition of Vectors?
A body may be subjected upon various vectors acting simultaneously upon it. It is very cumbersome and difficult to analyze the effect of each vector separately. So, the vectors are required to be added together to get the cumulative effect of all the vectors acting on that body. This is called “addition of vectors”.
Therefore, addition of Vectors is the operation of adding two or more vectors together, into a single vector whose effect is the same as that of the cumulative effect of component vectors before addition.
The single vector, which we will get after addition of many vectors, is called a “Resultant Vector”.
As the vectors have magnitude and direction both, so they cannot be added by using simple rules of algebra or arithmetic. Vectors can be added by two different methods. These are called as –
- Geometrical method of addition of vectors.
- Analytical methods of addition of vectors by resolving them into components.
Resultant Vector
A single vector, which we get after addition of many vectors by specified rules of vector addition, is called a Resultant Vector.
Therefore, the resultant vector of two or more vectors is defined as that single vector which will produce the same effect as if the individual vectors together would produce.
The process of adding of two or more vectors is also called as composition of vectors.
Geometrical Methods of Addition of Vectors
Geometrical or graphical method is conveniently used for addition of two or more vectors. Three laws of vector addition are used.
- Triangle law of vector addition for adding two vectors.
- Parallelogram law of vector addition for adding two vectors.
- Polygon law of vector addition for adding more than two vectors.
Triangle Law of Vector Addition
Triangle law of addition of vector is a convenient method to find the resultant of two vectors. It is stated as –
If two vectors can be represented in magnitude and direction both by the two sides of a triangle taken in same order, then their resultant is represented completely in magnitude and direction by the third side taken in opposite order.
Consider about the action of two vectors acting on a particle as shown in figure. We wish to add the vectors ( \vec {P} ) and ( \vec {Q} ) to find its resultant vector by following the graphical rules of vector addition.
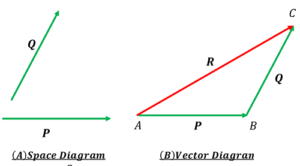
By taking a suitable scale called modulus for magnitude, we can draw a line AB parallel to the vector ( \vec {P} ) which will completely represent the vector ( \vec {P} ) in magnitude and direction both. Now line BC is drawn starting from point B and parallel to vector ( \vec {Q} ) which will completely represent the vector ( \vec {Q} ) in magnitude and direction both.
Now, if a triangle ( \triangle ABC ) is completed by drawing the third side AC , then the magnitude of side AC will give the magnitude of the resultant vector ( R ) and its direction will be from A to C i.e. in reverse order of completing the triangle.
This law is useful to find the resultant of two vectors.
Parallelogram Law of Vector Addition
Parallelogram law of vector addition is also used to find the resultant of two vectors.
It states that –
If two vectors are represented both in direction and magnitude by the two consecutive sides of a parallelogram drawn from a common point, then their resultant is completely represented by the diagonal of the parallelogram passing through that point.
Consider that, we have to add two vectors ( \vec { P } ) and ( \vec { Q } ) as shown in figure.
From a common point O , we draw a line ( OA ) equal and parallel to the vector ( \vec { P } ) and line ( OB ) equal and parallel to vector ( \vec { Q } ) . Now parallelogram OACB is completed. Then, diagonal OC will represent the resultant vector ( \vec { R } ) .
Therefore, \quad OC = OA + OB
So, \quad \vec { R } = \vec { P } + \vec { Q }
Polygon Law of Vector Addition
Polygon law of vector addition is useful to find the resultant of more than two vectors. Polygon law of addition of forces is stated as –
If a number of vectors are represented both in magnitude and direction by the sides of an open polygon taken in same order, then their resultant is represented both in magnitude and direction by closing side of the polygon taken in opposite order.
Suppose, we wish to add four vectors ( \vec {P_1} ), \ ( \vec {P_2} ), \ ( \vec {P_3} ) and ( \vec {P_4} ) as shown in figure.
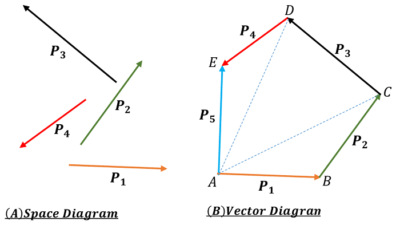
An open polygon ABCDE is drawn taking its sides in a scale proportional to the vectors and parallel to them. In the polygon ABCDE we have taken –
- Side AB = \left ( P_1 \right )
- Side BC = \left ( P_2 \right )
- Side CD = \left ( P_3 \right )
- Side DE = \left ( P_4 \right )
According to polygon law, the closing side AE of the polygon taken in the reverse order will represent the resultant ( \vec { R } ) .
Therefore, \quad AE = AB + BC + CD + DE
So, \quad \vec { R } = \vec { P_1 } + \vec { P_2 } + \vec { P_3 } + \vec { P_4 }
PROOF –
Here, we will apply triangle law of addition of vectors to different triangles of the polygon as shown in figure. In ( \triangle ABC ) we get –
AC = AB + BC = \vec {P_1} + \vec {P_2} .
Again, \quad AD = AC + CD = \vec {P_1} + \vec {P_2} + \vec {P_3}
And, \quad AE = AD + DE = \vec {P_1} + \vec {P_2} + \vec {P_3} + \vec {P_4}
Thus, \quad \vec {R} = \vec {P_1} + \vec {P_2} + \vec {P_3} + \vec {P_4}
Analytical Method of Addition of Vectors
In analytical method of addition of two or more vectors, trigonometrical relations are conveniently used to find the resultant vector. Before addition of the vectors, we require to resolve each vector in two common mutually perpendicular directions. This is called “Resolution of Vectors”.
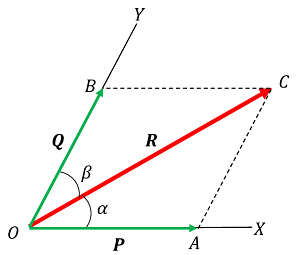
Consider about the parallelogram OACB drawn by two given vectors ( OA = \vec {P} ) and ( OB = \vec {Q} ) as shown in figure.
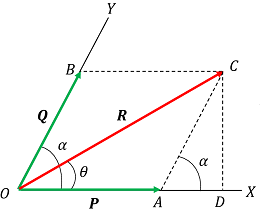
Let, ( \angle { AOB } = \alpha ) and ( \angle { AOC } = \theta ) . Perpendicular CD is drawn from point C which intersects at point D to the extension of side OA .
Since, AC is equal and parallel to OB , so we get AC = ( \vec {Q} )
Therefore, \quad \angle { DAC } = \angle { AOB } = \alpha
By trigonometric relations, we have –
AD = Q \cos \alpha \quad And \quad DC = Q \sin \alpha
Also, \quad OC^2 = ( OD^2 + DC^2 ) = \left [ \left ( OA + AD \right )^2 + DC^2 \right ]
Therefore, \quad R^2 = \left [ \left ( P + Q \cos \alpha \right )^2 + \left ( Q \sin \alpha \right )^2 \right ]
= \left [ P^2 + 2 P Q \cos \alpha + Q^2 \cos^2 \alpha + Q^2 \sin^2 \alpha \right ]
= \left [ P^2 + Q^2 + 2 P Q \cos \alpha \right ]
Therefore, \quad R = \sqrt {P^2 + Q^2 + 2 P Q \cos \alpha} . This equation gives the magnitude of resultant vector ( \vec {R} ) .
Now, let the resultant ( \vec {R} ) makes an angle ( \theta ) in positive direction with vector ( \vec {P} ) . Then –
\tan \theta = \left ( \frac{ DC }{ OD } \right ) = \left ( \frac { Q \sin \alpha }{ P + Q \cos \alpha } \right )
This equation gives the direction of resultant vector ( R ) with respect to the vector ( \vec {P} ) .
