“Gravitation” Numerical Problems
Try to solve the following “Gravitation” numerical problems to clear the concepts in solving the numerical problems.
First of all go to the theory portion of the respective topic and then try to solve the numerical problems by yourself. If facing problem in solving the numerical, click on the Go to solution button to see the ready made solution placed at the bottom of each numerical problem.
01) PROBLEM – P040101
Two lead spheres of ( 20 \ cm ) and ( 2 \ cm ) diameter respectively are placed with centres ( 100 \ cm ) apart. Calculate the attraction between them. Given the radius of the earth as ( 6.37 \times 10^{8} ) \ cm ) and its mean density as ( 5.53 \times 10^{3} kg \ m^{-3} ) . Specific gravity of lead is ( 11.5 ) .
What will happen if the lead spheres are replaced by brass spheres of same radii?
Keywords related to this problem.
02) PROBLEM – P040102
A body weighs ( 90 \ kgf ) on the earth surface. How much it will weigh on the surface of Mars whose mass is \left (\frac {1}{9} \right ) and radius is \left (\frac {1}{2} \right ) of that of the earth?
Keywords related to this problem.
03) PROBLEM – P040103
A man can jump ( 1.5 \ m ) high on the surface of earth. Calculate the approximate height he might be able to jump on a planet whose density is one-quarter that of the earth and whose radius is one-third of the earth’s radius.
Keywords related to this problem.
04) PROBLEM – P040104
Calculate the imaginary angular velocity of the earth for which effective acceleration due to gravity at the equator becomes zero. In this condition what will be the length of a day? Given, radius of the earth ( R = 6400 \ km ) and ( g = 10 \ m s^{-2} )
Keywords related to this problem.
05) PROBLEM – P040105
Two masses of ( 800 \ kg ) and ( 600 \ kg ) are at a distance of ( 0.25 \ m ) apart. Compute the magnitude of the intensity of the gravitational field at a point at distance ( 0.20 \ m ) from ( 800 \ kg ) mass and ( 0.15 \ m ) from the ( 600 \ kg ) mass.
Keywords related to this problem.
06) PROBLEM – P040106
Three point masses, each of mass ( m ) are placed at the vertices of an equilateral triangle of side ( l ) . What is the gravitational field and potential due to the three masses at the centroid of the triangle?
Keywords related to this problem.
07) PROBLEM – P040107
A remote sensing satellite of the earth revolves in a circular orbit at a height of ( 250 \ km ) above the earth’s surface. What is the (i) orbital speed and (ii) period of revolution of the satellite?
Take radius of the earth ( 6.38 \times 10^{6} m ) and acceleration due to gravity ( g = 9.8 \ m s^{-1} ) on the earth’s surface,
Keywords related to this problem.
08) PROBLEM – P040108
In a two stage launch of a satellite, the first stage brings the satellite to a height of ( 150 \ km ) and the second stage gives it the necessary critical speed to put it in a circular orbit around the earth. Which stage requires more expenditure of fuel? (Neglect damping due to air resistance, especially in the first stage).
Mass of the earth ( M = 6 \times 10^{24} kg ) . Radius of earth ( R = 6400 \ km ) and ( G = 6.67 \times 10^{-11} N m^2 kg^{-2} )
Keywords related to this problem.
09) PROBLEM – P040109
A ( 400 \ kg ) satellite is in a circular orbit of radius ( 2 R_E ) about the earth. How much energy is required to transfer it to a circular orbit of radius ( 4 R_E ) ? What are the changes in the kinetic and potential energies?
Keywords related to this problem.
10) PROBLEM – P040110
A cyclist comes to a skidding stop in ( 10 \ m ) . During this process, the force on the cycle due to the road is ( 200 \ N ) and is directly opposed to the motion.
(a) How much work does the road do on the cycle? (b) How much work does the cycle do on the road?
Keywords related to this problem.
11) PROBLEM – P040111
A woman pushes a trunk on railway platform which has a rough surface. She supplies a force of ( 100 \ N ) over a distance of ( 10 \ m ) . Thereafter she gets progressively tired and her applied force reduces linearly with distance to ( 50 \ N ) . The total distance by which the trunk has been moved is ( 20 \ m ) .
Plot the force applied by the woman and the frictional force which is ( 50 \ N ) . Calculate the work done by the two forces over ( 20 \ m ) .
Keywords related to this problem.
12) PROBLEM – P040112
If the linear momentum of a body increases by ( 20 \% ) , what will be the percentage increase in the kinetic energy of the body?
Keywords related to this problem.
13) PROBLEM – P040113
A ball is dropped to the ground from a height of ( 2 \ m ) . The coefficient of restitution is ( 0.6 ) .
To what height will the ball rebound?
Keywords related to this problem.
14) PROBLEM – P040114
A ball moving with a speed of ( 9 \ m / s ) strikes an identical ball such that after the collision the direction of each ball makes an angle 30 \degree with the original line of motion. Find the speeds of the two balls after the collision.
Is the kinetic energy conserved in the collision process?
Keywords related to this problem.
15) PROBLEM – P040115
A ( 0.5 \ kg ) mass particle moves along X axis from ( x = 5 \ m ) to ( x = 17.2 \ m ) under the influence of a force ( F_{(x)} ) . Where –
F_{(x)} = \left ( \frac {200}{2x + x^3} \right ) N
Estimate (at least 5 \% accuracy) the total work done by this force during this displacement.
Keywords related to this problem.
16) PROBLEM – P040116
A trolley of mass ( 200 \ kg ) moves with a uniform speed of ( 36 \ KMPH ) on a friction-less track. A child of mass ( 20 \ kg ) runs on the trolley from one end to the other ( 10 \ m ) away with a speed of ( 4 \ m / s ) relative to the trolley in a direction opposite to the trolley’s motion and jumps out of the trolley.
What is the final speed of the trolley? How much has the trolley moved from the time the child begins to run?
Keywords related to this problem.
17) PROBLEM – P040117
Two blocks A and B are connected to each other as shown in figure.
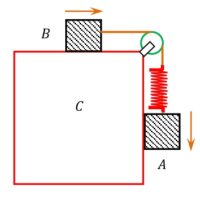
The string and spring are mass-less and pulley is friction-less. Block B slides over the horizontal top surface of stationary block C and the block A slides along the vertical slide of C both with same uniform speed. The coefficient of friction between the blocks is ( 0.2 ) and the spring constant of spring is ( 1960 \ N / m ) . If mass of block A is ( 2 \ kg ) , calculate (i) the mass of block B and (ii) energy stored in spring.
Keywords related to this problem.
18) PROBLEM – P040118
A ball moving on a horizontal friction-less plane hits an identical ball at rest with a velocity of ( 5 \ m \ s^{-1} ) . If the collision is elastic, calculate the speed imparted to the target ball if the speed of the projectile after the collision is ( 30 \ cm \ s^{-1} ) .
Show that the two balls will move at right angles to each other after the collision.
Keywords related to this problem.
