Doppler Effect

What is called “Doppler effect”?

If there is a relative motion between the source of sound and the observer, the frequency of sound felt by the observer is different from the frequency of sound emitted by the source. This phenomenon is popularly known as Doppler effect.

The apparent change in frequency of sound, when the sound source and the observer are in relative motion is called Doppler effect.

Let, us consider five different situations where Doppler effect is noticed –

Sound source is moving towards an stationary observer.
Source is moving away from an stationary observer.
Observer is moving towards an stationary sound source.
The observer is moving away from an stationary sound source.
Observer and sound source, both are moving towards each other.

Source is moving towards observer

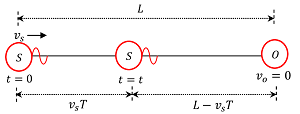
Consider about the figure shown below.

A sound source $S$ is moving with a speed $( v_s )$ towards an stationary observer at $O$ . Let –

$( \nu )$ is the frequency of vibration of the source.
$( v )$ is the velocity of sound in the medium.
$( v_s )$ is the velocity of sound source.
$( T )$ is the time period of the vibrations of sound source.

Assume that, at time $( t = 0 )$ , the sound source is at a distance $( L )$ from the observer.

Then, first sound pulse will reach the observer at time –

$t_1 = \left ( \frac { L }{ v } \right )$

The sound source will emit second pulse after time $( T )$ of the first pulse. In the mean time, the source will move a distance $( s = v_s T )$ towards the observer.

The distance between source and observer is now –

$L - s = L - v_s T$ .

So, the second pulse will reach the observer at time –

$t_2 = T + \left ( \frac {L - v_s T}{v} \right )$

061701 SOURCE IS MOVING TOWARDS STATIONARY OBSERVER

Therefore, time interval between two successive pulses felt by the observer will be –

$T' = ( t_2 - t_1 )$

$= \left [ T + \left ( \frac {L - v_s T}{v} \right ) - \left ( \frac {L}{v} \right ) \right ]$

$= \left [ T - \left ( \frac {v_s T}{v} \right ) \right ]$

$= T \left ( 1 - \frac {v_s}{v} \right ) = T \left ( \frac {v - v_s}{v} \right )$

Therefore, the apparent frequency of the sound felt by the observer will be –

$\nu' = \left ( \frac {1}{T'} \right ) = \left ( \frac {1}{T} \right ) \left ( \frac {v}{v - v_s} \right )$

$= \nu \left ( \frac {v}{v - v_s} \right )$ ……… (1)

So, $\quad \nu' > \nu \quad \text {because} \quad ( v - v_s ) < v$

Hence, the frequency of sound appears to increases when the source moves towards the stationary observer.

Source is moving away from observer

If the sound source is moving with speed $( v_s )$ away from the stationary observer then the apparent frequency of sound can be obtained by replacing $( v_s )$ by $( - v_s )$ in equation (1).

Therefore, $\quad \nu' = \nu \left ( \frac {v}{v + v_s} \right )$ ……… (2)

So, $\quad \nu' < \nu \quad \text {because} \quad ( v + v_s ) > v$

Hence, the frequency of sound appears to decreases when the source moves away from the stationary observer.

Observer is moving towards source

Consider about the figure shown below.

A sound source $S$ is stationary and a observer $O$ is moving towards the sound source. Let, $( v_o )$ is the velocity of moving observer.

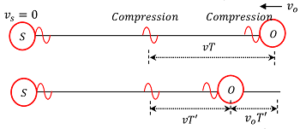
061702 OBSERVER IS MOVING TOWARDS STATIONARY SOURCE

At any instant the distance between two successive pulses will be $( \lambda = v T )$ . When the observer receives one pulse, the next pulse is at distance $( v T )$ away from him. The second pulse is moving towards observer with sound velocity $( v )$ . Also the observer is moving towards the pulse with a speed of $( v_o )$ .

Relative velocity of pulse with respect to observer will be $( v + v_o )$ . Therefore, time between two successive pulses received by the observer will be –

$T' = \left [ \frac {v T}{(v + v_o)} \right ]$

$= T \left [ \frac {v}{(v + v_o)} \right ]$

This is the time period of pulses felt by the observer. Hence, the apparent frequency of the sound heard by the observer will be –

$\nu' = \left ( \frac {1}{T'} \right ) = \left ( \frac {1}{T} \right ) \left ( \frac {v + v_o}{v} \right )$

$= \nu \left ( \frac {v + v_o}{v} \right )$ ………. (3)

Clearly $\quad \nu' > \nu \quad \text {because} \quad ( v + v_0 ) > v$

Hence, the frequency of sound appears to increases when the observer moves towards the stationary source.

Observer is moving away from source

If the observer is moving with speed $( v_o )$ away from the stationary source, then the apparent frequency of sound can be obtained by replacing $( v_o )$ by $( - v_o )$ in equation (3).

Therefore, $\quad \nu' = \nu \left ( \frac {v - v_o}{v} \right )$ ……… (4)

So, $\quad \nu' < \nu \quad \text {because} \quad ( v - v_o ) < v$ .

Hence, the frequency of sound appears to decreases when the observer moves away from the stationary source.

Observer and source both are moving to each other

Consider about the figure shown below. Observer and sound source both are moving towards each other. Let –

$( v_o )$ is the velocity of moving observer towards source.
$( v_s )$ is the velocity of moving sound source towards observer.

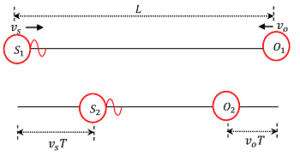
061703 SOURCE AND OBSERVER BOTH MOVING TO EACH OTHER

At time $( t = 0 )$ , the observer and the source are at positions $( O_1 )$ and $( S_1 )$ respectively. Assume that, the distance between them is $( L )$ . Since, the observer is moving towards the source, so the relative speed of the first pulse with respect to the observer will be $( v + v_o )$ .

Therefore, the observer will receive the first pulse at time –

$t_1 = \left ( \frac {L}{v + v_o} \right )$

Source will emit the second pulse after time $( T )$ . In time $( T )$ , the source has moved a distance of $( v_s T )$ and the observer has moved a distance of $( v_o T )$ . Hence, the new distance between them is now –

$L - T ( v_s + v_o )$

So, the second pulse will reach the observer after time –

$t_2 = T + \left [ \frac { L - T ( v_s + v_o ) }{ ( v + v_o ) } \right ]$

Thus, the time interval between two successive pulse received by the observer is –

$T' = ( t_2 - t_1 )$

$= T + \left [ \frac { L - T \left ( v_s + v_o \right ) }{ ( v + v_o ) } \right ] - \left ( \frac {L}{v + v_o} \right )$

$= T \left [ 1 - \left ( \frac { v_s + v_o }{ v + v_o } \right ) \right ]$

$= T \left ( \frac { v - v_s }{ v + v_o } \right )$

Hence, the apparent frequency of the sound felt by the observer is –

$\nu' = \left ( \frac { 1 }{ T' } \right )$

$= \left ( \frac { 1 }{ T } \right ) \left ( \frac { v + v_o }{ v - v_s } \right )$

$= \nu \left ( \frac { v + v_o }{ v - v_s } \right )$ ……… (5)

So, $\quad \nu' > \nu \quad \text {because} \quad ( v + v_o ) > ( v - v_s )$ .

Hence, the frequency of sound appears to increases when the observer and source both moves towards each other.

Asymmetrical Doppler effect

Doppler effect in case of sound wave is asymmetric in nature. From equations (1) and (2), we concluded that –

If the observer is stationary and sound source is moving with a speed of $( v' )$ towards the observer, then the apparent frequency is $\left [ \nu' = \nu \left ( \frac {v}{v - v'} \right ) \right ]$
In case the sound source is stationary and observer moves with the same speed of $( v' )$ towards the source, then the apparent frequency is $\left [ \nu " = \nu \left ( \frac {v + v'}{v} \right ) \right ]$
So we notice that $[ \nu' \ne \nu" ]$

This is called asymmetric Doppler effect.

For this reason the Doppler effect in sound is said to be asymmetric while Doppler effect in light is symmetric.

No Doppler effect

It is noticed that there is no change in observed frequency by an observer if –

Both the source and the observer move in the same direction with the same speed.
Either the source or the observer is at centre of a circle and the other is moving along the circumference with uniform speed.
Both source and observer are at rest and the medium moves ( i.e. when wind is blowing ).

This is called “No Doppler Effect.”

See numerical problems based on this article.