What is called a Vector?
In one dimensional motion, only two directions are possible. So, the directional aspect of the quantities like position, displacement, velocity and acceleration are taken care by using ( \pm ) signs before the quantities. But in case of motion in two dimensions ( i.e. a planer motion ) or three dimensions ( i.e. motion in space ), an object may have a different directions for different quantities simultaneously. In order to effectively dealing with such situations, we need to introduce the concept of a new physical quantity called vectors in which we take care of both the magnitude and direction of quantities.
Scalar & Vector Quantities
Physical quantities are of two types –
- Scalar quantity.
- Vector quantity.
Scalar Quantity
The physical quantities which have only magnitude and no direction are called scalar quantities or scalars.
A scalar quantity can be specified by a single number along with the unit of measurement. Examples – Mass, volume, density, time, temperature, electric current etc. are scalar quantities.
Vector Quantity
The physical quantities which have magnitude and direction both are called vector quantities or vectors.
A vector quantity is specified by a number with a unit of measurement and its direction. Examples – Displacement, velocity, force, momentum etc. are vector quantities.
Representation of a Vector
A vector quantity is represented by a straight line with an arrowhead over it. The length of the line gives the magnitude and the arrowhead gives the direction.
Suppose, a body has a velocity of ( 40 \ km \ h^{-1} ) towards East. If a length of ( 1 \ cm ) is chosen to represent a velocity of ( 10 \ km \ h^{-1} ) , then a line ( OA = 4 \ cm ) in length and drawn towards East with arrowhead at A will completely represent the velocity of the body as shown in figure.
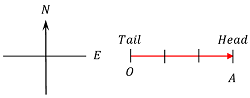
The point A is called head or terminal point of the vector and point O is called tail or initial point of the vector ( \vec {OA} ) .
In a simple notation a vector is represented by a single letter of alphabet with an arrow over it.
EXAMPLE –
A force vector can be represented as ( \vec {F} ) .
Types of Vectors
Vectors are broadly classified into two types –
- Polar vectors.
- Axial vectors.
Polar Vectors
The vectors which have a starting point or a point of application are called polar vectors.
Example – Displacement, velocity, force etc. are polar vectors.
Axial Vectors
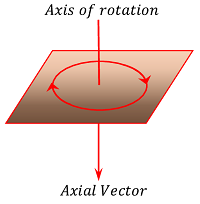
The vectors which represent rotational effect and act along the axis of rotation in accordance with right hand screw rule are called axial vectors.
Example – Angular velocity, torque, angular momentum, etc. are axial vectors.
As shown in figure, an axial vector will have its direction along its axis of rotation depending on its anticlockwise or clockwise rotational effect.
Vectors are further classified as –
- Position vector.
- Displacement vector.
Position Vectors
A vector which gives position of an object with reference to the origin of a co-ordinate system is called position vector.
The position vector provides two information –
- It tells about the straight line distance of the object from the origin O .
- It tells about the direction of the object with respect to the origin.
Displacement Vectors
It is a vector which tells that, how much and in which direction an object has changed its position in a given time interval.
The displacement vector provides two information –
- It tells about the straight line distance between the starting point and end point of journey of the object from the origin O .
- It tells the direction of the displacement of the object with respect to the origin.
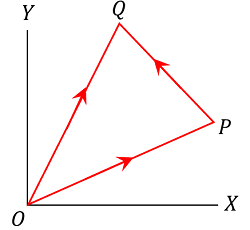
Consider about an object moving in XY plane. Suppose, initially at instant ( t = 0 ) , the object is at point P . Then OP will represent the position vector of object at instant ( t = 0 ) .
Let, in time interval ( t ) , the object has displaced and takes the final position at point Q as shown in figure. Then OQ will represent the position vector for final position of the object at instant ( t = t ) .
Then, vector PQ will represent the displacement vector of the object in time interval of ( t ) .
Therefore, \quad PQ = ( OQ - OP ) . Hence, displacement vector is obtained by subtracting the initial position vector from the final position vector.
Magnitude of Vectors
The magnitude of a vector is specified by the product of two quantities –
- Modulus of vector.
- Unit vector.
Modulus of a Vector
The modulus of a vector means the length or the magnitude of that vector. It is a scalar quantity.
Therefore, Modulus of vector \quad \vec {A} = | \vec {A} | = A
Unit Vector
A unit vector is a vector of unit magnitude drawn in the direction of a given vector.
A unit vector in the direction of a given vector is found by dividing the vector by its modulus.
Thus a unit vector in the direction of vector \vec {A} is given by –
\hat {A} = \left ( \frac { \vec {A}}{ | \vec {A} | } \right ) = \left ( \frac { \vec {A}}{A} \right )
A unit vector in the direction of a given vector \vec {A} is written as \hat {A} and is pronounced as ‘A carat’ or ‘A hat’ or ‘A cap’.
Any vector can be expressed as the modulus multiplied by the unit vector along its own direction.
Therefore, \quad \vec {A} = | \vec {A} | \times \hat {A}
Zero Vector
A zero vector or null vector is a vector that has zero magnitude and an arbitrary direction. It is represented by \vec {0} .
Properties of Zero Vectors
(1) When a vector is added to a zero vector, we will get the same vector.
Therefore, \quad \vec {A} + \vec {0} = \vec {A}
(2) When, a real number ( \lambda ) is multiplied by a zero vector, we will get a zero vector.
Therefore, \quad \lambda \times \vec {0} = \vec {0}
(3) When, a vector is multiplied by zero, we will get a zero vector.
Therefore, \quad \vec {A} \times 0 = \vec {0}
(4) If, ( \lambda ) and ( \mu ) are two different non zero real numbers, then the relation ( \lambda \vec {A} = \mu \vec {B} ) will be correct only if –
( \vec {A} ) \ \& \ ( \vec {B} ) both are zero vectors.
Examples of Zero Vector
- The position vector of a particle lying at the origin is a zero vector.
- The velocity vector of a stationary object is a zero vector.
- The acceleration vector of an object moving with uniform velocity is a zero vector.
Base Vector

In a right handed Cartesian coordinate system, three unit vectors ( \hat i ), \ ( \hat j ), \ ( \hat k ) are used to represent the positive directions of X axis, Y axis and Z axis respectively as shown in figure.
These three mutually perpendicular unit vectors are collectively known as orthogonal triad of unit vectors or base vectors.
Thus \quad | \hat i | = | \hat j | = | \hat k | = 1
Properties of Vectors
A vector has following properties –
Multiplication Law of Vector
When a vector ( \vec {A} ) is multiplied by a real number ( \lambda ) we get another vector ( \lambda \vec {A} ) .
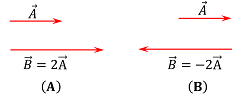
- The magnitude of ( \lambda \vec {A} ) is ( \lambda ) times the magnitude of vector ( \vec {A} ) .
- If ( \lambda ) is positive, then the direction of ( \lambda \vec {A} ) is same as that of ( \vec {A} ) .
- If ( \lambda ) is negative, then the direction of ( \lambda \vec {A} ) is opposite to that of ( \vec {A} ) .
Figure (A) shows multiplication of vector ( \vec {A} ) by a real positive number ( \lambda = 2 ) and figure (B) shows multiplication by a real negative number ( \lambda = - 2 )
If, ( \lambda ) is a pure number having no units or dimensions, then the unit of the product ( \lambda \vec {A} ) will be the same as that of ( \vec {A} ) .
However, when a vector ( \vec {A} ) is multiplied by a scalar ( \lambda ) which has certain units, then the units of product ( \lambda \vec {A} ) are obtained by multiplying the units of ( \vec {A} ) by the units of ( \lambda ) .
EXAMPLE –
When velocity vector is multiplied by mass (which is a scalar quantity having units), we get momentum. The units of momentum are obtained by multiplying the units of velocity and mass.
Commutative Law of Vector addition
Let two vectors ( \vec {A} ) and ( \vec {B} ) are added to get resultant vector ( \vec {C} ) .
Therefore, \quad \vec {A} + \vec {B} = \vec {C}
If we add the vectors in reverse manner in a way that ( \vec {B} + \vec {A} ) , we will get the same resultant vector ( \vec {C} )
Therefore, \quad \vec {A} + \vec {B} = \vec {B} + \vec {A}
This is called commutative law of vector addition.
Associative Law of Vector addition
Let, three vectors ( \vec {A} ), \ ( \vec {B} ) and ( \vec {C} ) are added to get resultant vector ( \vec {R} ) .
Therefore, \quad \vec {A} + \vec {B} + \vec {C} = \vec {R}
If we add any of two vectors first and then add their sum to the third vector in different manner, then we will get the same resultant vector ( \vec {R} ) .
Therefore, \quad ( \vec {A} + \vec {B} ) + \vec {C} = \vec {A} + ( \vec {B} + \vec {C} ) = \vec {R} .
This is called associative law of vector addition.
