What is called Amplitude of a Wave?
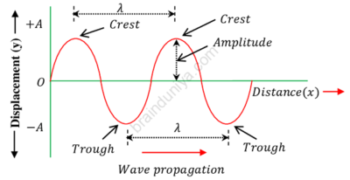
In a wave propagation, particles of the medium oscillates / vibrates to and fro about their mean position. The mean position is called equilibrium position. The displacement of the particle is measured by the distance from its mean position. When the particle is at mean position, its displacement is zero. The maximum displacement is at the extreme positions of the motion. Amplitude of a wave is the maximum distance covered on either side of the mean position by the medium particles.
Therefore, amplitude of a wave motion is defined as the maximum displacement made by the vibrating medium particles about their mean position.
Amplitude of wave is an important parameter by which properties of wave motions are specified. It is denoted by ( A ) . A medium particle covers a total distance of 4 / A , during one complete cycle of vibration.
Consider about the displacement-distance curve of a wave pulse as shown in figure. In the figure, ( O ) represents the mean position of vibrating medium particles. Therefore, amplitude of wave is the maximum displacement of vibrating medium particles. It is from ( O ) \ \text {to} \ ( + A ) in positive direction and from ( O ) \ \text {to} \ ( - A ) in negative direction of displacements from mean position.
Properties of Wave Motion
Along with amplitude of wave, some other parameters of wave motion are also important by which the properties of wave are specified. These are –
- Time period of wave motion.
- Frequency of wave motion.
- Wavelength of wave motion.
- Wave number.
- Propagation constant.
- Wave velocity etc.
Time Period of Wave Pulse
Consider about the displacement-distance curve of a wave pulse as shown in figure. In the figure, two complete cycles of wave pulses are shown.
Time period is the time taken to complete one complete cycle of oscillation or vibration by the medium particles.
It is denoted by ( T ) .
Frequency of Wave Pulse
Frequency is the number of waves produced per unit time. It is the reciprocal of time period and denoted by ( \nu )
Therefore, \quad \nu = \left ( \frac { 1 }{ T } \right )
Angular Frequency
The rate of change of phase with time is called angular frequency of the wave motion. It is denoted by ( \omega )
We know that, change in phase in time ( T ) is ( 2 \pi ) . Therefore, angular frequency will be –
\omega = \left ( \frac { 2 \pi }{ T } \right ) = 2 \pi \nu
When a wave propagates through a medium, all the medium particles oscillate about their mean position identically but they remain in different phases. Phase of one oscillating particle is different than the phase of its adjacent particles.
Wavelength
Wavelength is defined as the distance covered by a wave during the time in which the medium particle completes one cycle of vibration. It is denoted by ( \lambda )
It may also be defined as the distance between two nearest particles of the medium which are vibrating in the same phase.
Wave number
It is the count of number of waves present in unit distance of medium. It is denoted by ( \bar { \nu } ) .
Wave number is equal to the reciprocal of wavelength. Therefore, \quad \bar { \nu } = \left ( \frac { 1 }{ \lambda } \right ) .
Propagation constant
The quantity \left ( \frac { 2 \pi }{ \lambda } \right ) is called angular wave number or propagation constant of a wave. It is denoted by ( k ) .
Therefore, \quad k = \left ( \frac {2 \pi }{ \lambda } \right )
Wave Velocity
The distance covered by a wave per unit time is called wave velocity or phase velocity. It is denoted by ( v ) .
We know that, medium particle completes one cycle in time ( T ) . In this time interval, wave pulse travels a distance equal to the wavelength ( \lambda ) .
Therefore, wave velocity \quad v = \frac {\text {Distance}}{\text {Time}}
Or, \quad v = \left ( \frac { \lambda }{ T } \right )
But, \quad \nu = \left ( \frac { 1 }{ T } \right )
Therefore, \quad v = \nu \lambda
\text {Wave velocity} = \text {Frequency} \ \times \ \text {Wavelength}
Transverse Wave Motion in a Stretched String
Wave motion in a stretched string or rope is a transverse wave.
Hence, it is expressed by two factors –
- Tension ( T ) in the string which is the measure of elasticity in the string. Wave cannot propagate in a string without tension.
- Linear mass density ( m ) i.e. mass per unit length of the string which can store kinetic energy of wave propagation.
The speed of transverse wave through a stretched string is given by –
v = \sqrt { \frac { T }{ m }}
Ripples in a rope, vibration of guitar string etc. are examples of wave motion through a stretched string.
DIMENSIONAL CHECK
Dimension of tension ( T ) is [M L T ^ { - 2 }] . Dimension of mass per unit length ( m) is \left ( \frac { Mass }{ Length } \right ) = [M L ^ { - 1 }] .
Therefore, dimension of wave speed will be –
\sqrt { \frac { Dimension \ of \ T }{ Dimension \ of \ m }}
= \left ( \frac { M L T ^ { -2 } }{ M L ^ { - 1 } } \right ) ^ { \frac { 1 }{ 2 } }
= [ L T ^ { - 1 } ] = Dimension of linear speed.
Transverse Wave Motion through Solids
In solid bodies, a propagating wave can be a form of transverse wave.
The speed of transverse wave through a solid is expressed by two factors –
- Modulus of rigidity ( \eta ) of solid body.
- Mass per unit volume or density ( \rho ) .
The speed of transverse wave through a solid is given by –
v = \sqrt { \frac { \eta }{ \rho }}
Secondary waves or seismic waves during earthquake are the examples of transverse waves through solids.
DIMENSIONAL CHECK
Dimension of ( \eta ) is [M L ^ { - 1 } T ^ { - 2 }] . Dimension of ( \rho ) is \left ( \frac { Mass }{ Volume } \right ) = [M L ^ { - 3 }]
Therefore, dimension of wave speed will be –
\sqrt { \frac { \eta }{ \rho }} = \left ( \frac { M L ^ { - 1 } T ^ { - 2 } }{ M L ^ { - 3 } } \right ) ^ { \frac { 1 }{ 2 } }
= [ L T ^ { - 1 } ] = Dimension of linear speed.
Longitudinal Wave Motion through Solids
In solid bodies, a propagating wave can be a form of longitudinal wave.
The speed of longitudinal wave through a solid is expressed by two factors –
- Modulus of compression or elongation i.e., Young’s modulus of elasticity ( \gamma ) of the solid.
- Mass per unit volume or density ( \rho ) .
The speed of longitudinal wave through a solid is given by –
v = \sqrt { \frac { \gamma }{ \rho }}
Propagation of sound waves through solid materials, waves in helical springs etc. are examples of longitudinal waves through solids.
DIMENSIONAL CHECK
Dimension of ( \gamma ) is [M L ^ { - 1 } T ^ { - 2 }] . Dimension of ( \rho ) is \left ( \frac { Mass }{ Volume } \right ) = [M L ^ { - 3 }]
Therefore, dimension of wave speed will be –
\sqrt { \frac { \gamma }{ \rho }} = \left ( \frac { M L ^ { - 1 } T ^ { - 2 } }{ M L ^ { - 3 } } \right ) ^ { \frac { 1 }{ 2 } }
= [ L T ^ { - 1 } ] = Dimension of linear speed.
Longitudinal Wave Motion through Fluids
In fluid bodies, the propagating wave is a longitudinal wave.
The speed of longitudinal wave through liquids and gases are expressed by two factors –
- Volume elasticity or Bulk modulus ( k ) of the solid.
- Mass per unit volume or density ( \rho ) .
The speed of longitudinal waves through liquids and gases are given by –
v = \sqrt { \frac { k }{ \rho }}
Sound waves through liquids and gases are examples of longitudinal waves through fluids.
DIMENSIONAL CHECK
Dimension of Bulk modulus ( k ) is [M L ^ { - 1 } T ^ { - 2 }] . Dimension of density ( \rho ) is \left ( \frac { Mass }{ Volume } \right ) = [M L ^ { - 3 }]
Therefore, dimension of wave speed will be –
\sqrt { \frac { k }{ \rho }} = \left ( \frac { M L ^ { - 1 } T ^ { - 2 } }{ M L ^ { - 3 } } \right ) ^ { \frac { 1 }{ 2 } }
= [ L T ^ { - 1 } ] = Dimension of linear speed.
See numerical problems based on this article.
