What is called Resolution of Vectors?
In analyzing the vector problems, sometimes we require to evaluate the effect of a vector in certain directions of our interest. This is done by resolution of vector in required directions. It is just an opposite process of addition of vectors. The vectors formed after splitting are called component vectors.
Therefore, resolution is the process of splitting of a vector into two or more vectors in such a way that their combined effect is same as that of the given vector.
The resolution of a vector is just opposite to the addition of vectors. It means dividing the vector into components. A component of a vector in any direction gives a measure of the effect of the given vector in that direction.
Component Vectors
By resolution of a vector, we get two vectors in certain direction as per our requirement. The split out vectors are called component vectors.
Consider about a vector ( R ) which is acting along line OC as shown in figure. Suppose we have to find the components of this vector along the directions OX and OY .
Let, the line of directions OX and OY are making angles ( \alpha ) and ( \beta ) respectively with the line of action OC of vector ( R ) .
We draw the lines –
- CA parallel to OY meeting the line OX at point A .
- CB parallel to OX meeting the line OY at point B .
Then, OA and OB will represent the components of vector ( \vec {R} ) along the directions OX and OY respectively.
Let, ( OA = \vec {P} ) and ( OB = \vec {Q} ) are the components of vector ( \vec {R} ) as shown in vector diagram.
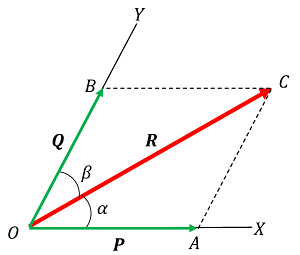
From geometry of the diagram, we have –
\angle {OCA} = \angle {BOC} (Alternate angles).
= \left [ 2 \pi - \left ( \alpha + \beta \right ) \right ]
Let, \quad \left ( \alpha + \beta \right ) = \theta
Therefore, \quad \angle {OAC} = \left ( 2 \pi - \theta \right )
Application of Sin Law
Applying sin law in ( \triangle OAC ) , we will get –
\left [ \frac { OA }{ \sin \beta } \right ] = \left [ \frac { AC }{ \sin \alpha } \right ] = \left [ \frac { OC }{ \sin ( 2 \pi - \theta ) } \right ]
By trigonometrical ratios, we have –
\sin ( 2 \pi - \theta ) = \sin \theta
Therefore, \left [ \frac { P }{ \sin \beta } \right ] = \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \theta \right ) } \right ]
= \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
= \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
Also, \quad \left [ \frac { Q }{ \sin \alpha } \right ] = \left [ \frac { R }{ \sin \left ( \alpha + \beta \right ) } \right ]
Therefore, \quad P = \left [ \frac { R \sin \beta }{ \sin \left ( \alpha + \beta \right )} \right ] \quad and \quad Q = \left [ \frac { R \sin \alpha }{ \sin \left ( \alpha + \beta \right )} \right ]
Rectangular Components of a Vector
If, a vector is resolved in two directions which are mutually perpendicular to each other, then the resolved components are called “Rectangular Components of Vector”.
Therefore, if we resolve a vector in the direction of two mutually perpendicular directions by analytical and graphical methods, then component vectors so obtained are called rectangular components.
Suppose, we wish to resolve the vector ( \vec {R} ) in rectangular components along the directions OX and OY .

Since, ( \angle XOY = 90 \degree ) and ( \angle XOC = \alpha ) .
Therefore, \quad \left [ \beta = \left ( 90 \degree - \alpha \right ) \right ]
Hence, \quad \left ( \frac{ P }{ R } \right ) = \cos \alpha
Or, \quad P = R \cos \alpha ……. (1)
And, \quad \left ( \frac{ Q }{ R } \right ) = \cos \beta = \cos \left ( 90 \degree - \alpha \right )
By trigonometrical ratios, we have –
\cos ( \pi - \alpha ) = \sin \alpha
Therefore, \quad \left ( \frac{ Q }{ R } \right ) = \sin \alpha
Or, \quad Q = R \sin \alpha ……. (2)
Therefore, from equation (1) and (2) we get –
- Rectangular component vector ( \vec {P} ) in a direction inclined at an angle ( \alpha ) to ( \vec {R} ) is ( P = R \cos \alpha )
- Rectangular component vector ( \vec {Q} ) in a direction inclined at an angle \left ( \beta )\right ) to ( \vec {R} ) is ( Q = R \cos \beta = R \sin \alpha )
Rectangular Components in three dimensions
If, a vector is resolved in three directions which are mutually perpendicular to each other, then the resolved components are called “Rectangular Components of Vector in three dimension”.
Therefore, if we resolve a vector in three directions, namely X, \ Y \ \& \ Z axes, which are mutually perpendicular to each other, then component vectors so obtained are called rectangular components in three dimensions.
Consider that a vector ( \vec {A} ) is represented by ( OP ) as shown in figure.

Taking O as origin, we construct a rectangular parallelopiped with its three edges along the three rectangular axes i.e. X, \ Y \ \& \ Z axes. Then, ( \vec {A} ) will represent the diagonal of the parallelopiped whose intercepts along X, \ Y \ \& \ Z axes are ( \vec {A_x} ), \ ( \vec {A_y} ) \ \& \ ( \vec {A_z} ) respectively.
Therefore, vectors ( \vec {A_x} ), \ ( \vec {A_y} ) \ \& \ ( \vec {A_z} ) are the three rectangular components of vector ( \vec {A} ) .
Applying triangle law of vectors, we will get –
OP = OT + TP
Applying parallelogram law of vectors, we will get –
OT = OR + OQ
Therefore, \quad OP = OR + OQ + TP
But, \quad TP = OS
Hence, \quad OP = OR + OQ + OS
So, \quad \vec {A} = \vec {A_x} + \vec {A_y} + \vec {A_z}
= A_x \hat i + A_y \hat j + A_z \hat k
Let, ( \alpha ), \ ( \beta ) and ( \gamma ) are the angles between the vector ( \vec {A} ) and X, \ Y \ \& \ Z axes respectively. Then we have –
- A_x = A \cos \alpha
- A_y = A \cos \beta
- A_z = A \cos \gamma
Magnitude of Vector in three dimension
From the geometry of the figure, we note that –
{OP}^2 = {OT}^2 + {TP}^2
= {OQ}^2 + {QT}^2 + {TP}^2
So, \quad {A}^2 = {A_x}^2 + {A_y}^2 + {A_z}^2
Or, \quad A = \sqrt {{A_x}^2 + {A_y}^2 + {A_z}^2}
Position of Vector in three dimension
A position vector ( \vec {r} ) in three dimensions can be expressed as –
\vec {r} = x \hat {i} + y \hat {j} + z \hat {k}
Where, ( x ), \ ( y ) \ \& \ ( z ) are the components of ( \vec {r} ) along X, \ Y \ \& \ Z axes respectively.
