What is meant by Thermal Conductivity?
Thermal conductivity is the property which regulates the process of heat transfer in solid objects by mode of heat conduction.
The fundamental law of thermal conductivity and heat conduction was presented by Fourier. Hence, the law is called, Fourier’s law of heat conduction.
Fourier’s law
Consider about a cubical block having cross section area ( A ) and thickness ( L ) .
Suppose, that the opposite faces of the cube are at temperatures ( T_1 ) and ( T_2 ) . Let, ( T_1 > T_2 ) .
Fourier’s law of heat conduction states that –
The amount of heat ( Q ) , that flows from hot surface at ( T_1 ) towards cold surface at ( T_2 ) during the steady state will be –
- Directly proportional to the cross sectional area ( A ) .
- Proportional to the temperature difference of the surfaces i.e. \left ( T_1 - T_2 \right ) .
- Directly proportional to the time ( t ) for which the heat flows.
- Inversely proportional to the thickness ( L ) of the block.
- Depends upon the nature of the material of the block.
Therefore, combining all of the the above conditions, we get –
Q \propto \left [ \frac{ A \left (T_1 - T_2 \right ) t }{ L } \right ]
Or, \quad Q = K \left [ \frac { A \left (T_1 - T_2 \right ) t }{ L } \right ]
Coefficient of Thermal Conductivity
From Fourier’s law of heat conduction, we get –
Q = K \left [ \frac { A \left (T_1 - T_2 \right ) t }{ L } \right ]
The proportionality constant K is called coefficient of thermal conductivity for the given material. Its value depends on the nature of the material of body.
If, \quad A = 1, \ ( T_1 - T_2 ) = 1, \ t = 1 and L = 1
Then, \quad Q = K
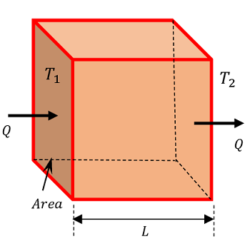
Hence, the coefficient of thermal conductivity of a material is defined as the quantity of heat that flows per unit time through a unit cube of the material, when its opposite faces are kept at a temperature difference of one degree.
Therefore, \quad K = \left [ \frac{ Q L }{ A \left (T_1 - T_2 \right ) t } \right ]
Units of coefficient of thermal conductivity are –
- In SI system \quad J s^{-1} m^{-1} K^{-1} \quad or \quad W m^{-1} K^{-1}
- In CGS system \quad cal \ s^{-1} cm^{-1} \degree C^{-1}
Application of Thermal Conduction
Some applications of thermal conductivity in our daily life are explained below.
- In winter, the human body is at higher temperature than surrounding. Hence, a metallic handle feels colder than a wooden door because heat flows from human body to metallic handle.
- Wood or Bakelite is bad conductor of heat. So handles for cooking utensils are made up of these materials for heat resisting and easy handling.
- Ice is packed in saw dust. Saw dust and air trapped in it are poor conductor of heat and prevent ice to melt from outside temperature.
- Copper is a good conductor of heat. Therefore when a wire gauge made of copper wire is placed over the burning Bunsen’s burner, the flame doesn’t go beyond the gauge because copper wire absorbs most of the heat.
- Fiber glass is poor conductor or insulator of heat. Hence the walls of refrigerator, heaters, coolers etc are packed with these type of materials to resist flow of heat to or from the atmosphere.
Heat Current
Flow of heat through a thermal conductor is very much similar to flow of electric current through an electric conductor. Similarities between these processes are –
- Electrical charge flows in a circuit due to potential difference between its two ends. Similarly heat flows in a conductor due to temperature difference between two points.
- The flow of charge per unit time is called electric current. Similarly the flow of heat per unit time is called heat current.
- Electrical resistance is the ratio of potential difference and electric current. Similarly thermal resistance is the ratio of temperature difference and heat current.
Therefore, the flow of heat per unit time is called heat current.
Thus, \quad H = \left ( \frac { Q }{ t } \right )
But, \quad Q = KA \left ( \frac { \Delta T }{ L } \right ) t
Therefore, \quad H = \left [ \frac { KA \left ( \frac { \Delta T }{ L } \right ) t}{t} \right ]
Or, \quad H = KA \left ( \frac {\Delta T}{ L } \right )
SI unit of heat current is ( Js^{-1} ) (joule per second) or ( W ) (Watt)
Thermal Resistance
The ratio of temperature difference to the heat current between two points of a heat conductor is called thermal resistance.
Therefore, \quad R_{H} = \left ( \frac { \Delta T }{ H } \right )
But, \quad H = KA \left ( \frac {\Delta T}{ L } \right )
Therefore, \quad R_{H} = \left [ \frac { \Delta T }{ KA \left ( \frac {\Delta T}{ L } \right ) } \right ]
Or, \quad R_{H} = \left ( \frac { L }{KA} \right )
Hence, greater the coefficient of thermal conductivity of a material smaller will be the thermal resistance of that material.
Series combination of Thermal Conductors
Let, ( n ) number of slabs each of cross sectional area ( A ) and lengths l_1, \ l_2 \ .... etc. are connected in series as shown in figure.
Let, thermal conductivity of these slabs are K_1, \ K_2 \ .... etc. respectively are connected in series as shown in figure.
Since same quantity of heat current is flowing through each of the conductors, so it is called a series combination of thermal conductors. Heat flowing through each slab is same.
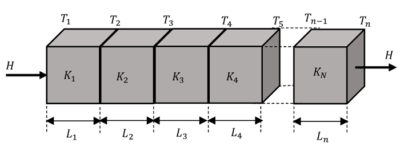
Therefore, for slabs –
H_1 = H_2 = ....... = \left ( \frac{ Q }{ t } \right )
Or, \quad \left [ \frac {K_1 A (T_1 - T_2 )}{l_1} \right ] = \left [ \frac {K_2 A (T_2 - T_3 )}{l_2} \right ] = \ ...... \ = \left [ \frac { Q }{ t } \right ]
Or, \quad \left [ \frac { (T_1 - T_2 )}{l_1 / K_1 A} \right ] = \left [ \frac {(T_2 - T_3 )}{l_2 / K_2 A} \right ] = \ ...... \ = \left [ \frac { Q }{ t } \right ]
But, \quad R = \left ( \frac {L}{KA} \right )
Therefore, \quad \left [ \frac {(T_1 - T_2 )}{R_1} \right ] = \left [ \frac {(T_2 - T_3 )}{R_2} \right ] = \ ...... \ = \left [ \frac { Q }{ t } \right ]
Hence, \quad (T_1 - T_2 ) = \left ( \frac {Q R_1}{t} \right ), \quad (T_2 - T_3 ) = \left ( \frac {Q R_2}{t} \right ) \ ......
Also, total temperature difference for the combined slab is –
( T_n - T_1 )
But, \quad ( T_n - T_1 ) = ( T_1 - T_2 ) + ( T_2 - T_3 ) + ......
Therefore, \quad ( T_n - T_1 ) = \left ( \frac {Q R_1}{t} \right ) + \left ( \frac {Q R_2}{t} \right ) + ......
Or, \quad ( T_n - T_1 ) = \left ( \frac {Q}{t} \right ) \left ( R_1 + R_2 + ...... \right )
Let, ( R_S ) is the equivalent thermal resistance of the combined slab. Then –
( T_n - T_1 ) = \left ( \frac {Q R_S}{t} \right )
Therefore, equivalent thermal resistance for a combination of thermal conductors in series will be –
R_S = ( R_1 + R_2 + ...... )
Equivalent Thermal Conductivity in Series
Assume that, ( K_S ) is the equivalent thermal conductivity for series combination of conductors.
Then, \left [ R_S = \left ( \frac {L}{K_S A} \right ) \right ]
Also, \quad R_1 = \left ( \frac {L_1}{K_1 A} \right ), \quad R_2 = \left ( \frac {L_2}{K_2 A} \right )
Therefore, \quad \left ( \frac {L}{K_S A} \right ) = \left ( \frac {L_1}{K_1 A} \right ) + \left ( \frac {L_2}{K_2 A} \right ) + \ .... \
Or, \quad K_S A = \left [ \frac { ( L_1 + L_2 + .... ) }{ \left ( \frac {L_1}{K_1 A} + \frac {L_2}{K_2 A} + ..... \right )} \right ]
= \left [ \frac { A L }{ \left ( \frac {L_1}{K_1 } + \frac {L_2}{K_2 } + ..... \right ) } \right ]
So, \quad K_S = \left [ \frac { L }{ \left ( \frac {L_1}{K_1 } + \frac {L_2}{K_2 } + ..... \right ) } \right ]
Therefore, equivalent thermal conductivity of combination of slabs in series is given by –
K_S = \left [ \frac { L }{ \left ( \frac {L_1}{K_1 } + \frac {L_2}{K_2 } + ..... \right ) } \right ]
Now, consider a series combination of thermal conductors in which the length of each slab is equal to ( L ) . Then total length of the slab will be ( n \ L )
Then, equivalent thermal conductivity of the combination will be –
K_S = \left [ \frac {n}{ \left ( \frac {1}{K_1 } + \frac {1}{K_2 } + ..... \right ) } \right ]
For two slabs of equal lengths –
K_S = \left [ \frac {2}{ \left ( \frac {1}{K_1 } + \frac {1}{K_2 } \right ) } \right ]
= \left [ \frac {2 K_1 K_2}{( K_1 + K_2 )} \right ]
Parallel combination of Thermal Conductors
Let, ( n ) number of slabs each of cross sectional area ( A_1, \ A_2, \ .... ) and each of length ( l ) and thermal conductivity ( K_1, \ K_2, \ .... ) respectively are connected as shown in figure.
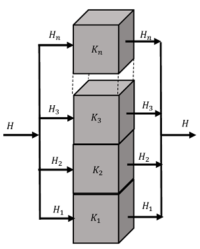
Since quantity of heat current flowing through each of the conductors is different, so it is called a parallel combination.
Difference in temperature ( \Delta T ) is same for all conductors and total heat flow ( H ) is divided into the slabs depending upon their thermal conductivity.
Let, equivalent thermal resistance of the parallel combination is ( R_P ) . Then –
H = ( H_1 + H_2 + ....... )
But, \quad H = \left ( \frac {\Delta T}{R_P} \right ) \quad H_1 = \left ( \frac {\Delta T}{R_1} \right ) and so on.
Therefore, \quad \left ( \frac {\Delta T}{R_P} \right ) = \left ( \frac {\Delta T}{R_1} \right ) + \left ( \frac {\Delta T}{R_2} \right ) + .......
Or, \quad \left ( \frac {1}{R_P} \right ) = \left ( \frac {1}{R_1} \right ) + \left ( \frac {1}{R_2} \right ) + .......
Therefore, equivalent thermal resistance for a combination of thermal conductors in parallel is given by –
\left ( \frac {1}{R_P} \right ) = \left ( \frac {1}{R_2} \right ) + \left ( \frac {1}{R_2} \right ) + .......
Equivalent Thermal Conductivity in Parallel
Let, ( K_P ) is the equivalent thermal conductivity of the parallel combination.
Then, from Fourier’s law –
H = K_P A \left ( \frac {\Delta T}{L} \right )
Also, \quad H_1 = K_1 A_1 \left ( \frac {\Delta T}{L} \right ) etc.
Therefore, \quad K_P A \left ( \frac {\Delta T}{L} \right ) = \left [ K_1 A_1 \left ( \frac {\Delta T}{L} \right ) + K_2 A_2 \left ( \frac {\Delta T}{L} \right ) + ...... \right ]
Or, \quad K_P A = ( K_1 A_1 + K_2 A_2 + ....... )
Also, \quad A = ( A_1 + A_2 + .... )
Therefore, \quad K_P ( A_1 + A_2 + ....... ) = ( K_1 A_1 + K_2 A_2 + ....... )
Or, \quad K_P = \left [ \frac { \left ( K_1 A_1 + K_2 A_2 + ..... \right ) }{\left ( A_1 + A_2 + .... \right ) } \right ]
For ( n ) slabs of equal area –
K_P = \left [ \frac { ( K_1 + K_2 + ..... ) }{n} \right ]
For ( n ) slabs of equal area and equal thermal conductivity –
K_P = \left ( \frac { ( nK ) }{n} \right ) = K
Equivalent thermal conductivity for two slabs of equal area will be –
K = \left [ \frac { ( K_1 + K_2 ) }{2} \right ]
See numerical problems based on this article.
