What is called Mechanical Advantage?
Mechanical advantage of machine is defined as the ratio of load lifted at output end to the effort applied at the input end of the machine.
Therefore, \quad \text {Mechanical Advantage} = \left ( \frac{\text {Output force}}{\text {Input force}} \right )
= \left ( \frac {\text {Load}}{\text {Effort}} \right )
Mechanical Advantage is simply written as MA.
Ideal Mechanical Advantage of machine
In ideal conditions, friction is neglected. But, all machines have some friction and a part of applied effort is lost in overcoming this friction.
Therefore, \quad \text {Actual effort} = \text {Ideal effort} + \text {Effort lost in friction}
Ideal mechanical advantage of a machine is defined as the ratio of load to the ideal effort for the machine.
Hence, \quad \text {Ideal Mechanical A} = \left ( \frac {\text {Load}}{\text {Ideal Effort}} \right )
- Ideal effort is less than actual effort.
- Therefore, Ideal MA of a machine is greater than actual MA.
Mechanical Advantage of Simple Machines
In this article, detail process is explained to find the MA of some simple machines.
MA of Wedge
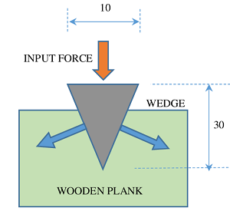
Woodcutter’s Axes is a simple example of a wedge.
Consider about an axes as shown in figure. When an effort is applied on the head of axes, it digs into the wood.
If we apply an effort ( P ) on axes head, it penetrates producing forces perpendicular to its inclined surfaces as shown in figure. Let, the resistance offered by the wood is ( W ) .
Let, the width of the head of axes is ( w ) and its length is ( h ) . Then, for complete digging of the axes, distance moved by the effort will be ( h ) and distance moved by the load will be ( w )
We know that, \quad \text {work done} = \text {Force} \ \times \ \text {displacement}
Then, work done by the effort is ( P \times h ) and work output in overcoming the resistance of wood is ( W \times w )
Therefore, by the law of conservation of energy we have –
\text {Work Input} = \text {Work Output}
So, \quad ( P \times h ) = ( W \times w )
Or, \quad \left ( \frac {W}{P} \right ) = \left ( \frac {h}{w} \right )
Hence, \quad MA = \left ( \frac {h}{w} \right )
Therefore, Mechanical advantage of a wedge is determined by dividing its length by its width.
MA = \left ( \frac{\text {Length of wedge}}{\text {Width of wedge}} \right )
Therefore, MA of axes shown in figure will be –
MA = \left ( \frac {30}{10} \right ) = 3
If angle of wedge is more acute or narrow, then ratio of its length and width will be greater and so, the mechanical advantage will be more.
MA of Inclined Plane
Consider about an inclined plane as shown in figure. A body of mass ( M ) is being lifted up to height ( H ) . For this purpose, the body is pushed along the slant surface of the inclined plane with a force ( F ) .
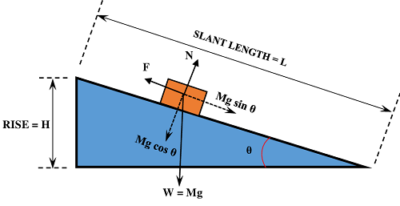
In ideal conditions if there is no friction force, the required push will be equal to the component ( Mg \sin \theta ) of weight of body which is parallel to slant surface.
So, \quad F = W \sin \theta = M g \sin \theta
Therefore, ideal MA of inclined plane will be –
MA = \left ( \frac {\text {Weight lifted}}{\text {Applied \ force}} \right )
= \left ( \frac { Mg }{ Mg \sin \theta } \right )
= \left ( \frac { 1 }{ \sin \theta } \right )
But, \quad \sin \theta = \left ( \frac{ H }{ L } \right )
Therefore, \quad MA = \left [ \frac { 1 }{ \left ( \frac { H }{ L } \right ) } \right ]
= \left ( \frac { L }{ H } \right )
So, ideal mechanical advantage of an inclined plane is also given by –
= \left ( \frac{\text {Slant length}}{\text {Height of plane}} \right )
MA of Wheel & Axle
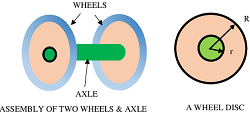
Consider about a wheel and axle arrangement as shown in figure.
Let, a force ( F_{Input} ) is applied tangentially to the surface of the wheel disc of radius ( R ) .
Then, turning effect or torque developed in disc will be –
T_{Wheel} = F_{Input} \times R
If, there is no friction, then same torque will be transmitted to the axle.
Therefore, \quad T_{Axle} = T_{Wheel}
Let, ( F_{Output} ) is the force developed at surface of axle.
Then, turning effect or torque developed in axle will be –
T_{Axle} = F_{Output} \times r
So, \quad F_{Output} \times r = F_{Input} \times R
Or, \quad \left ( \frac {F_{Output}}{F_{Input}} \right ) = \left ( \frac {R}{r} \right )
Therefore, MA of Wheel & Axle will be –
MA = \left ( \frac {F_{Output}}{F_{Input}} \right )
= \left ( \frac {R}{r} \right )
Mechanical advantage of wheel and axle is the ratio of radius of wheel over radius of axle.
MA of Screw
Consider about a screw as shown in figure. Diameter of the screw cylinder is ( d ) . On its body surface, an inclined plane is wrapped which forms thread on the cylinder surface.
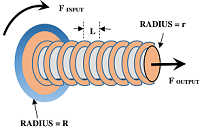
Let, radius of screw head is ( R ) . The lead or pitch of screw is ( L ) . ( Lead or pitch is the measure of axial distance of advancement of nut for one complete rotation of screw. )
In general, \quad \text {Lead of screw} = n \times \text {pitch} .
Where ( n ) is the number of starts of thread.
Since, lead or pitch of screw is similar to Rise or Height ( H ) of an inclined plane. Therefore, when screw is rotated for one complete turn, it advances or retracted about a distance ( L ) .
Let, a force ( F_{Input} ) is applied on the head of the screw. Then for one complete rotation of the screw –
Input work = F_{Input} \times 2 \pi R
If, ( F_{Output} ) is the generated force by screw then –
Output work = F_{Output} \times L
If, friction is negligible, then –
Output Work = Input Work.
Therefore, \quad F_{Output} \times L = F_{Input} \times 2 \pi R
Or, \quad \left ( \frac {F_{Output}}{F_{Input}} \right ) = 2 \pi \left ( \frac {R}{L} \right )
Therefore, MA of screw is given by –
MA = \left ( \frac {F_{Output}}{F_{Input}} \right )
= 2 \pi \left ( \frac {R}{L} \right )
MA of Compound Machines
A compound machine or a complex machine is made up of series of components. Each component is basically a simple machine. It may be a lever, a screw, a wedge, an inclined plane or a wheel & axle etc.
Thus, if a machine is a combination of 2 components, then its mechanical advantage will be –
MA_{compound} = MA of component 1 × MA of component 2
Similarly, if a machine is a combination of ( n ) components, then –
Mechanical advantage = MA of component 1 × MA of component 2 × ….. × MA of component ‘n’
Therefore, Mechanical Advantage of a compound machine = Product of individual Mechanical Advantages of each components.
