How to determine Intensity of electric field of a Dipole?
Intensity of an electric field produced by an electric dipole is called dipole field intensity.
Dipole field intensity of dipole is of great importance at a point which may lie –
- On axial position of dipole called – “End-on position”.
- On a perpendicular bisector of dipole length i.e. equatorial line called – “Broad-on position”.
Dipole Field Intensity at End-on position
Consider an electric dipole AB consisting of charge ( - q ) \text {and} ( + q ) . The distance between two charges is ( 2l ) as shown in figure.
Now, consider a point P at a distance ( r ) from the centre O of the dipole on axial line AB . Electric field intensity at point P due to the charge ( + q ) will be –
E_{( + q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{BP^2} \right )
But, \quad BP = ( r - l )
So, \quad E_{( + q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q}{( r - l )^2} \right ]
This is acting along the direction from B \ \text {to} \ P . Electric field intensity at point P due to charge ( - q ) will be –
E_{( - q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{AP^2} \right )
But, \quad AP = ( r + l )
So, \quad E_{( - q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q}{( r + l )^2} \right ]
This is acting along the direction from A \ \text {to} \ P
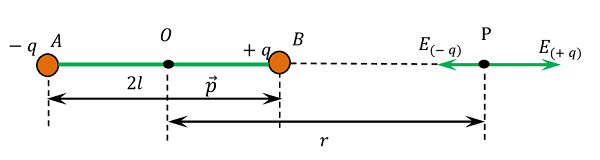
The net electric field intensity at P will be the vector sum of field intensities by individual charges.
So, \quad E = \left [ E_{( + q )} + E_{( - q )} \right ]
= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q}{( r - l )^2} + \frac {q}{( r + l )^2} \right ]
= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {( r + l )^2 - ( r - l )^2}{( r^2 - l^2 )^2} \right ]
= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {4 r l}{( r^2 - l^2 )^2} \right ]
= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {2 r ( q \times 2 l )}{( r^2 - l^2 )^2} \right ]
But \quad ( q \times 2 l ) = p (Dipole moment). Therefore, field intensity at end-on position of a dipole is given by –
E = \left [ \frac {2r p}{4 \pi \epsilon_0 ( r^2 - l^2 )^2} \right ] ……… (1)
Dipole Field Intensity at infinity of End-on position
When, the point P lies a far distance from the point O such that, ( r >> l ) . Then, \quad \left ( r \pm l \right ) \cong r
So, \quad \left ( r^2 - l^2 \right ) \cong r^2
Putting this value in equation (1), we will get –
E = \left ( \frac {2r p}{4 \pi \epsilon_0 r^4} \right )
= \left ( \frac {2p}{4 \pi \epsilon_0 r^3} \right ) ……… (2)
Hence, \quad E \propto \left ( \frac {1}{r^3} \right )
Dipole Field Intensity at Broad-on position
Consider about an electric dipole AB consisting of charge ( - q ) \ \text {and} \ ( + q ) separated by a distance ( 2l ) as shown in figure.
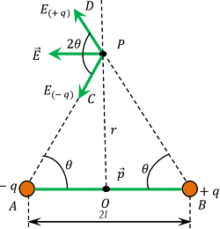
Now, consider about a point P on the equatorial line at a distance ( r ) from the centre O . Distance of point P from point A or B will be –
AP = BP = x
Also, \quad x^2 = ( r^2 + l^2 )
Electric field intensity at point P due to the charge ( + q ) will be –
E_{( + q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{x^2} \right )
= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q}{\left ( r^2 + l^2 \right )} \right ] ……… (1)
This is acting along the direction from P \ \text {to} \ D . Electric field intensity at point P due to the charge ( - q ) will be –
E_{( - q )} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{x^2} \right )
= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q}{\left ( r^2 + l^2 \right )} \right ] ……… (2)
This is acting along the direction from P \ \text {to} \ C .
From equation (1) and equation (2), we conclude that, forces E_{( + q )} and E_{( - q )} are equal and angle included between them is ( 2 \theta ) . So, the resultant can be find by using parallelogram law of addition of forces.
Therefore, \quad E = \sqrt {E^2_{( + q )} + E^2_{( - q )} + 2 \times E_{( + q )} \times E_{( - q )} \times \cos 2 \theta }
= \sqrt {2 E^2_{( + q )} + 2 E^2_{( + q )} . \cos 2 \theta }
= \sqrt {2E^2_{( + q )} \left ( 1 + \cos 2 \theta \right )} = \sqrt {2 E^2_{( + q )} \times 2 \cos^2 \theta }
= 2 E_{( + q )} \cos \theta = 2 \times \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2 + l^2} \right ) \cos \theta
Now, from triangle ( \triangle {OAP} ) , we will get –
\cos \theta = \left ( \frac {l}{\sqrt {r^2 + l^2}} \right )
Therefore, \quad E = 2 \times \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r^2 + l^2} \right ) \left ( \frac {l}{\sqrt {r^2 + l^2}} \right )
= \left [ \frac {q \times 2l}{4 \pi \epsilon_0 \left ( r^2 + l^2 \right )^{\frac {3}{2}}} \right ]
But, \quad \left ( q \times 2l \right ) = p . Therefore, field intensity at broad-on position of a dipole is given by –
E = \left [ \frac {p}{4 \pi \epsilon_0 \left ( r^2 + l^2 \right )^{\frac {3}{2}}} \right ] ……. (3)
Field Intensity at infinity in Broad-on position
When, the point P lies a far distance from the point O , then \left ( r >> l \right )
Then, \quad \left ( r^2 + l^2 \right ) \cong r^2
Putting this value in equation (3), we will get –
E = \left ( \frac {p}{4 \pi \epsilon_0 r^3} \right ) ……… (4)
Therefore, \quad E \propto \left ( \frac {1}{r^3} \right )
Dipole Field Intensity at arbitrary position
A general equation can be derived which gives the field intensity of a dipole at any arbitrary position.
Consider about an electric dipole AB having dipole moment ( \vec {p} ) . P is any point which is at a distance ( r ) from the centre O of the dipole. Let, the line OP makes an angle ( \theta ) with the direction of dipole moment as shown in figure.
Resolving dipole moment ( \vec {p} ) into components, we will get –
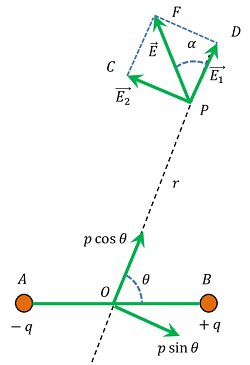
- Component ( p \cos \theta ) which is acting along OP
- Component ( p \sin \theta ) which is acting perpendicular to OP .
Point P is on axial line with respect to ( p \cos \theta ) . So electric field intensity at P due to this component will be –
E_1 = \left ( \frac {2 p \cos \theta}{4 \pi \epsilon_0 r^3} \right ) .
This is acting along direction from P \ \text {to} \ D as shown in figure. Point P is on equatorial line with respect to ( p \sin \theta ) . So electric field intensity at P due to this component will be –
E_2 = \left ( \frac {p \sin \theta}{4 \pi \epsilon_0 r^3} \right ) .
This is acting along direction from P \ \text {to} \ C as shown in figure. Since, ( E_1 ) and ( E_2 ) are perpendicular to each other, so the resultant electric field intensity at P will be –
E = \sqrt { E^2_1 + E^2_2 }
= \sqrt { \left ( \frac {2 p \cos \theta}{4 \pi \epsilon_0 r^3} \right )^2 + \left ( \frac {p \sin \theta}{4 \pi \epsilon_0 r^3} \right )^2 }
= \left ( \frac { p }{4 \pi \epsilon_0 r^3} \right ) \sqrt {\left (4 \cos^2 \theta + \sin^2 \theta \right )}
= \left ( \frac { p }{4 \pi \epsilon_0 r^3} \right ) \sqrt {\left (3 \cos^2 \theta + 1 \right )}
Direction of Dipole Electric Field
Let, the net electric field of dipole ( \vec {E} ) makes an angle ( \alpha ) with ( \vec {E_1} ) .
Then, \quad \tan \alpha = \left ( \frac {FD}{PD} \right ) = \left ( \frac {\vec {E_2}}{\vec {E_1}} \right ) .
= \left ( \frac {p \sin \theta}{4 \pi \epsilon_0 r^3} \right ) \left ( \frac {4 \pi \epsilon_0 r^3}{2 p \cos \theta} \right )
= \left ( \frac {1}{2} \right ) \tan \theta
This gives the direction of net electric field of dipole.
