What is meant by “Acceleration due to Gravity”?
Earth attracts all bodies near its surface by a force of gravity called gravitational force. The acceleration produced by this force is called earth’s acceleration due to gravity.
- By Newton’s laws of gravitational force, we have –
F = G \left ( \frac {m_1 m_2 }{ r ^2 } \right ) .
Consider that a body of mass ( m ) is kept on the earth’s surface. Radius and mass of the earth are ( R ) \ \text {and} \ ( M ) respectively.
- Then, earth’s gravitational pull on the body will be –
F = G \left ( \frac {M m }{ R ^2 } \right ) .
Let, earth’s gravitational pulling force produces an acceleration ( g ) on the body.
- Then by Newtons laws of motion, we get –
F = ( mg )
Therefore, \quad F = G \left ( \frac {M m }{ R^2 } \right ) = ( mg )
- Hence, acceleration produced by the earth is –
g = G \left ( \frac {M}{ R^2 } \right )
This acceleration is called acceleration due to gravity.
Variation of Acceleration due to Gravity
Value of acceleration due to gravity acting on a body varies with the location of body on the earth’s surface, above the earth’s surface or below it.
This variation is due to the following effects –
- Effect of location on earth’s surface.
- Effect of earth’s rotation.
- Effect of height from earth surface.
- Effect of depth under earth surface.
1.Effect of location on Earth’s surface
Acceleration due to gravity varies with the location on the earth’s surface.
Consider that a point mass ( m ) is situated on the earth’s surface. Then, its distance from earth’s centre will be ( r = R ) .
- Therefore, gravitational force on the point mass will be –
F = G \left ( \frac { M m }{ R^2 } \right )
Suppose the mass ( m ) experiences an acceleration of ( g ) .
- According to Newton’s Second Law of motion, we have –
\text {Force} = \text {Mass} \ \times \ \text {Acceleration}
Therefore, \quad F = mg
Or, \quad mg = G \left ( \frac { M m }{ R^2 } \right )
Therefore, \quad g = G \left ( \frac { M }{ R^2 } \right )
- This equation gives the acceleration due to gravity on the surface of earth. We see that –
g \propto \left ( \frac {1}{R} \right )
Earth is not a perfect sphere but it is flattened at the poles. So, the equatorial radius ( R_e ) of earth is greater than the polar radius ( R_p ) . It has found that [ ( R_e - R_p ) = 21 \ km ] .
This is the reason that, acceleration due to gravity at equator is less than acceleration due to gravity at poles.
- Therefore, \quad ( g_e < g_p )
Near the surface of earth, the standard value of acceleration due to gravity is taken as ( 9.8 \ ms^{ -2 } ) \quad or \quad ( 32 \ fts^{ -2 } )
2.Effect of Earth Rotation
Consider about the figure showing the rotation of earth.
As the earth rotates about its polar axis with angular velocity ( \omega ) , every particle laying on its surface also revolves along horizontal circles with the same angular velocity ( \omega ) .
Consider about a particle of mass ( m ) laying at point P whose latitude is ( \lambda ) .
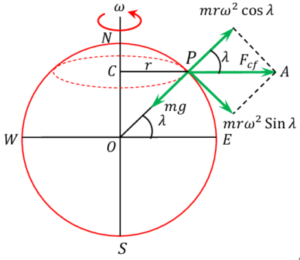
With rotation of earth, the particle P describes a horizontal circle of radius ( r ) where –
r = PC = R \cos \lambda
- The centrifugal force acting along PA on the particle is given by –
F_{cf} = ( mr \omega^2 )
This force has two components –
- Component force ( mr \omega^2 \cos \lambda ) – This force is acting opposite to the direction of weight ( mg ) of the particle.
- Component force ( mr \omega^2 \sin \lambda ) – This force is acting perpendicular to ( mg ) and has no effect on ( mg ) .
So, the apparent weight of the particle P is –
mg_{\lambda} = [ ( mg ) - ( mr \omega^2 \cos \lambda )
Or, \quad g_{\lambda} = ( g - r \omega^2 \cos \lambda )
But, \quad \left [ r = R \cos \lambda \right ]
- Therefore, \quad g_{\lambda} = ( g - R \omega^2 \cos^2 \lambda )
As ( \lambda ) increases, value of \left ( \cos \lambda \right ) decreases and ( g_{\lambda} ) increases.
So, as we move from equator to pole, the acceleration due to gravity increases. Therefore, acceleration due to gravity is minimum at the equator and maximum at the poles.
3.Effect of height from Earth surface
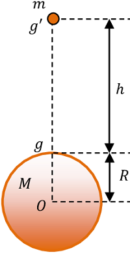
Consider about a point mass ( m ) situated at an height of ( h ) above the earth’s surface as shown in figure.
- The effective distance between centres of point mass and earth is –

040202 VARIATION OF GRAVITATIONAL ACCELERATION ON HEIGHT
r = \left ( R + h \right )
Therefore, the gravitational force on mass ( m ) will be –
F = G \left [ \frac { M m }{ \left ( R + h \right )^2 } \right ]
If ( g' ) is the acceleration due to gravity at that point, then –
m g' = G \left [ \frac { M m }{ \left ( R + h \right )^2 } \right ]
Or, \quad g' = \left [ \frac { G M }{ \left ( R + h \right )^2 } \right ]
- Dividing numerator and denominator by ( R^2 ) we have –
g' = \left [ \left ( \frac { G M }{ R^2} \right ) \right] \times \left [ \frac {1}{\frac {( R + h )^2}{R^2}} \right ]
= \left [ \left ( \frac { G M }{ R^2} \right ) \right] \times \left [ \frac {( R + h )}{R} \right ]^{-2}
= \left [ \frac { G M }{ R^2 } \left (1 + \frac { h }{ R } \right )^{-2} \right ]
= g \left [ 1 + \left ( \frac { h }{ R } \right ) \right ]^{ -2 }
Since, ( h << R ) so we can neglect higher power terms of \left ( \frac {h}{R} \right ) .
- Thus, \quad g' = g \left [ 1 - \left ( \frac { 2h }{ R } \right ) \right ]
Therefore –
- Value of acceleration due to gravity decreases with increase in height above the earth’s surface.
- When ( h ) is small i.e. \left ( h << R \right ) , then the fraction \left ( \frac { h }{ R } \right ) becomes negligible. Hence, the above equation reduces to ( g' = g )
4.Effect of depth under Earth surface
Consider that a point mass ( m ) is situated at a depth of ( h ) below the earth’s surface as shown in figure.
Then, according to Newton’s shell theorem, the outer shell has no effect on the point mass m kept at point P . Only the inner sphere of radius ( r ) will exert a force. Where ( r = R - h )
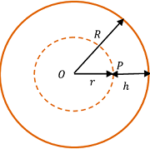
Then effective mass of earth ( m_r ) is concentrated at the centre.
- Thus, the gravitational force on mass ( m ) is –
F = G \left [ \frac { m_r m }{ \left ( R - h \right )^2 } \right ]
But, \quad m_r = \left ( \frac { 4 }{ 3 } \right ) \pi \left ( R - h \right )^3 \rho = \left ( \frac { 4 }{ 3 } \right ) \pi R^3 \rho \left ( \frac { R - h }{ R } \right )^3 = M \left ( \frac { R - h }{ R } \right )^3
Or, \quad m_r = M \left ( \frac { R - h }{ R } \right )^3
Therefore, gravitational force acting on the mass will be –
F = \left [ \frac { G m_r m }{ \left ( R - h \right )^2 } \right ]
= \left [ \frac { G m }{ \left ( R - h \right )^2 } \right ] \left [ M \left ( \frac { R - h }{ R } \right )^3 \right ]
= \left [ \frac { G M m }{ R^2 } \right ] \left [ \frac { R - h }{ R } \right ]
But, \quad F = m g' \quad And \quad \left [ \frac { G M }{ R^2 } \right ] = g
Therefore, \quad m g'= \left [ \frac { G M m }{ R^2 } \right ] \left [ \frac { R - h }{ R } \right ]
= m g \left [ \frac { R - h }{ R } \right ]
Or, \quad g' = g \left ( \frac { R - h }{ R } \right ) = g \left (1 - \frac { h }{ R } \right )
Therefore –
- Value of acceleration due to gravity decreases while going in depth inside earth.
- When ( h ) is small, i.e., \left ( h << R \right ) fraction \left ( \frac { h }{ R } \right ) becomes negligible. Hence, the above equation reduces to ( g' = g )
- At the centre of the earth ( h = R ) . Therefore, \left [ 1 - \left ( \frac { h }{ R } \right ) = 0 \right ] . Hence, at the centre of earth ( g' = g \times 0 = 0 ) . This is the reason that, weight of a body at earth’s centre becomes zero.
See numerical problems based on this article.