What are Sound Beats?
When two sound waves, having slightly different frequencies are made to travel along the same path in the same direction through same medium, they superpose upon each other and the intensity of the resultant sound increases and decreases with time in periodic fashion. This is called sound beats.
The periodic variations in the intensity of resultant sound caused by the superposing of two similar sound waves of slightly different frequencies are called sound beats.
One rise and one fall of intensity constitute one cycle of sound beats. The number of beats produced per second is called beat frequency.
Audible Sound Beats
Human brain retains the information received in it for some time. This is called persistence of hearing or persistence of vision etc.
Due to persistence of hearing, the sound signals received in brain remains for approximately \left ( \frac {1}{10} \right ) second. So human ear is not able to distinguish two different sounds if the time interval between them is less than \left ( \frac {1}{10} \right ) second.
Hence, beats heard will not be distinct if the number of sound beats produced per second is more than 10 . Thus for sound beats to be audible, the difference of frequencies of two superposing waves should not exceed 10 .
Formation of Sound Beats
Consider about the following figure. Two sound waves of frequencies ( \nu_1 ) and ( \nu_2 ) are made to superpose. Green colored time curve is the wave of frequency ( \nu_1 ) and red colored curve is for wave of frequency ( \nu_2 ) . Let, ( \nu_1 > \nu_2 ) .
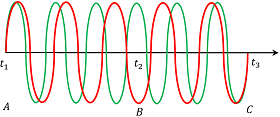
Assume that, at time ( t_1 ) , the two waves meet in the same phase. Hence, they will be constructive in nature and will produce maximum sound intensity.
With the pass of time, the phase difference between two waves increases gradually and a time ( t_2 ) , comes where two waves are exactly in opposite phases and will produce minimum sound intensity. Time interval ( t_2 ) is the time when one wave gains half of cycle of vibration over the other.
With more pass of time, the phase difference between two waves will goes on increasing and a time ( t_3 ) comes where two waves are again exactly in the same phase. This time ( t_3 ) is the time when one wave gains one full cycle of vibration over the other. At this instant, they will produce sound of maximum intensity again.
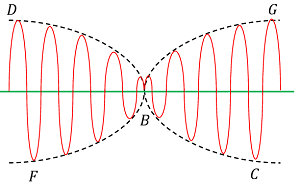
This process continues which results in producing sounds of varying intensity from maximum and minimum intensity in succession.
The displacement of the resultant wave is obtained by the principle of superposition given by –
y = ( y_1 + y_2 )
Beat Frequency
From discussion, time required to complete one beat cycle is time interval from ( t_1 ) to ( t_3 ) . This is called beat period.
In one beat period, the green wave has completed ( \nu + 1 ) cycles and red wave has completed ( \nu ) vibrations.
Therefore, 1 beat cycle = ( \nu + 1 ) cycles of green wave - ( \nu ) cycles of red wave.
\therefore \quad \text {Beat frequency} = \text {Difference in frequencies of the two superposing waves}Therefore, beat frequency is defined as the difference of frequencies of two superposing waves from which beat is produced.
Therefore, \quad \nu_{beat} = ( \nu_1 - \nu_2 )
Application of Sound Beats
Phenomenon of beat formation is useful in various applications. The most widely used applications are –
- Determination of unknown frequency of a tuning fork in laboratory.
- Tuning of musical instruments. Musicians use the beat phenomenon in tuning their musical instruments.
- Producing colorful effects in music.
- Detection of marsh gas in mines.
Determination of unknown frequency
Consider about an arrangement of two tuning forks A and B of nearly equal frequencies mounted on two sound boxes placed with their open ends facing to each other as shown in figure.
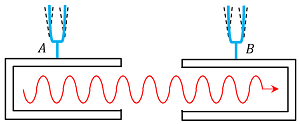
Suppose, \left ( \nu_1 \right ) is the known frequency of tuning fork A and ( \nu_2 ) is the unknown frequency of tuning fork B .
When the two tuning forks are sounded together let, they produce ( n ) beats per second.
Therefore, as per definition of beat frequency either ( \nu_2 ) is equal to ( \nu_1 + n ) or ( \nu_1 - n ) . This dilemma of frequency can be solved by one of the following two methods –
- Wax Loading Method.
- Filing Method.
Wax Loading Method
Attach a little wax to the prong of the tuning fork B and find the number of beats produced per second again.
Let, this time the number of beats produced per second is \left ( n' \right ) .
If, \quad \left ( n' < n \right ) \quad Then \quad \left ( \nu_2 = \nu_1 + n \right )
EXPLANATION
If, the frequency of B is greater than that of A , then the attaching of wax has resulted in lowering its frequency and in turn reduces the difference in frequencies of A and B . This would decrease the beat frequency.
Hence, after loading wax if the beat frequency decreases then the unknown frequency of tuning fork B is greater than the known frequency of tuning fork A .
Therefore, \nu_2 = ( \nu_1 + n )
Similarly, if the beat frequency increases after loading of wax then the unknown frequency of tuning fork B is lower than the known frequency of tuning fork A .
Therefore, \quad \nu_2 = ( \nu_1 - n )
Filing Method
In this method one prong of the tuning fork B is filed to increase its frequency. Again the number of beats produced per second ( n' ) is found out.
If, on filing of prong the beat frequency decreases i.e. if ( n' < n )
Then, \quad \nu_2 = ( \nu_1 - n )
EXPLANATION
If, the frequency of B is lesser than that of A then the filing of prong has resulted in increasing its frequency and in turn reduces the difference in frequencies of A and B . This would result decrease in the beat frequency.
Hence, if the beat frequency decreases after filing then the unknown frequency of tuning fork B is lesser than the known frequency of tuning fork A .
Therefore, \quad \nu_2 = ( \nu_1 - n )
Similarly if the beat frequency increases after filing, then the unknown frequency of tuning fork B is greater than the known frequency of tuning fork A.
Therefore, \quad \nu_2 = ( \nu_1 + n )
Music
The sound which has a pleasing sensation to the human ears is called a music.
Musical sound is produced by regular and periodic vibrations without any sudden change in amplitude e.g. sound produced by a violin, flute, tuning fork etc.
Noise
The sound which is harsh and has a non-pleasing sensation to the human ears is called a noise.
A noise consists of slow, irregular and non periodic vibrations, that may have a sudden change in amplitude e.g. sound produced by a gunshot, cracker bomb etc.
Characteristics of Sound
Different musical sounds are characterized and distinguished based upon the following parameters –
- Intensity.
- Threshold limit.
- Pitch.
- Quality.
- Loudness.
Intensity
Intensity of a sound at a point is defined as the amount of sound energy passing per unit time per unit area around that point in a perpendicular direction. It is denoted by ( I ) .
The intensity or loudness of a sound depends on the amplitude of vibrations. It determines the loudness or softness of a musical sound.
Threshold of hearing
The lowest intensity of sound that can be perceived by the human ear is called threshold of hearing. It is denoted by ( I_0 ) .
For a sound of frequency 1 \ k \ Hz , it is found that the threshold of hearing is 10^{- 12} \ W \ m^{- 2}
Pitch of Sound
It is the characteristic of musical sound that distinguish between a shrill note from a dull note.
Pitch determines the highness or lowness of a musical sound. It depends upon frequency of the vibration. The higher the frequency of vibration, the higher will be the tone.
Quality of Sound
It is the characteristic of musical sound that distinguish between two sounds from different sources but of same pitch and loudness.
Quality depends upon the nature of the vibrating body. It is dependent on the number and relative intensity of overtones produced by the vibrating body.
Loudness of Sound
Loudness is the characteristic of a musical sound by which we can distinguish between a loud sound and a faint sound.
It depends upon intensity of sound and denoted by ( L ) . The unit for loudness is bel.
The loudness of a sound is said to be 1 bel if its intensity is 10 times of threshold of hearing.
Therefore, loudness of sound of intensity ( I ) will be –
L = \log _ { 10 } \left ( \frac { I }{ I _ 0} \right )
Where, ( I_0 ) is the threshold of hearing. This is called Weber-Fechner law.
The practical unit of loudness is decibel (dB).
1 decibel = \left ( \frac {1}{10} \right ) bel.
Therefore, loudness of sound of intensity ( I ) in decibel will be –
L = 10 \log _ { 10 } \left ( \frac { I }{ I _ 0} \right )
See numerical problems based on this article.
