Laws of Cooling

What are Laws of Cooling of bodies?

If a material body is heated up to a very high temperature and then let to cool down, it will take a certain time to reach at a lower temperature. Amount of heat lost per unit time is called cooling rate or rate of cooling. For small temperature difference between a body and its surrounding, the rate of cooling of the body is directly proportional to the temperature difference and the surface area exposed.

The rate by which a body loses heat by radiation is called rate of cooling.

The rate of cooling depends upon the following factors –

1. Temperature of the cooling body.
2. Temperature of the surrounding.
3. Ambient conditions and wind speed.
4. Nature of surface of the body.
5. Surface area of the body.
6. Nature of material of the body.

Many laws have been formulated stating the time taken for cooling of a hot body in a given atmosphere. These are called laws of cooling. Among these laws, two are most important –

1. Newton’s laws of cooling.
2. Stefan Boltzmann’s law.

Newton’s Laws of Cooling

According to Newton’s Laws of Cooling, rate of cooling depends upon following factors –

1. Temperature of the body.
2. Temperature of the surrounding medium.
3. Nature and extent of exposed surface.

Let, a body of mass ( m ) at temperature ( T ) is kept in atmosphere at temperature ( T_0 ) .

Then, according to Newton’s law of cooling –

\text {Rate of loss of heat} \ \propto \ \text {Temperature difference}

So, \quad - \left ( \frac {dQ}{dt} \right ) \propto \left ( T - T_0 \right )

Thus, \quad - \left ( \frac {dQ}{dt} \right ) = k \left ( T - T_0 \right ) …….. (1)

From principle of calorimetry, expression for heat loss from a body is given by –

dQ = mc \ dT

Therefore, rate of heat loss or rate of cooling will be obtained by dividing both sides by ( dt ) . Thus –

\left ( \frac {dQ}{dt} \right ) = mc \left ( \frac {dT}{dt} \right ) ……… (2)

Comparing equations (1) and (2), we will get –

- mc \left ( \frac {dT}{dt} \right ) = k ( T - T_0 )

Or, \quad \left ( \frac {dT}{dt} \right ) = \left ( \frac {k}{mc} \right ) ( T - T_0 )

But \left ( \frac {k}{mc} \right ) is a constant. Let it is ( K ) . Then –

\left ( \frac {dT}{dt} \right ) = K ( T - T_0 )

Or, \quad \left [ \frac {dT}{( T - T_0 )} \right ] = - K \ dt

On integrating both sides, we will get –

\int \left [ \frac {1}{( T - T_0 )} \right ] dT = - K \int dt

Or, \quad \log \left ( T - T_0 \right ) = Kt + c ……. (3)

So, \quad ( T - T_0 ) = e^{- Kt + c}

Or, \quad T = T_0 + e^{c} e^{- Kt}

= T_0 + C e^{- Kt} ……. (4)

Equations (1), (2), (3) and (4) are different forms of mathematical representation of Newton’s law of cooling.

Cooling curves

Different curves obtained by following Newton’s laws of cooling are as follows –

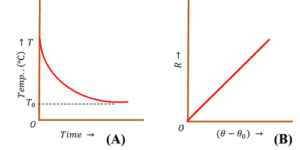
(A) Body Temperature and Time curve –

Consider about the “Body Temperature – Time curve” as shown in figure (A).

• Time is plotted along X axis and body temperature is plotted along Y axis.
• Clearly the rate of fall of body temperature is initially higher and decreases exponentially.
• Hence, cooling rate also decreases exponentially.

(B) Cooling Rate and Temperature difference curve –

Consider about the “Cooling Rate – Temperature difference” curve as shown in figure (B).

• Temperature difference ( \theta - \theta_0 ) is plotted along X axis and cooling rate ( R ) is plotted along Y axis.
• Clearly the relation is a straight line passing through origin.
• Rate of cooling is directly proportional to the temperature difference i.e. ( R \ \propto \ \Delta \theta )

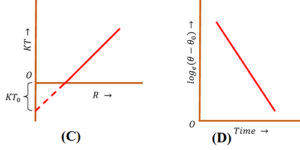
(C) Cooling Rate – Body Temperature curve –

Consider about the “Cooling Rate – Body Temperature” curve as shown in figure (C).

• Cooling rate ( R ) is plotted along X axis and body temperature ( KT ) is plotted along Y axis.
• Clearly the relation is a straight line which intercepts X axis.
• It indicates that rate of cooling is zero when ( T = T_0 )
• It also indicates that, cooling rate is negative when ( T < T_0 ) and for that portion of curve \left ( R = - KT_0 \right )

(D) Cooling Rate – Time curve –

Consider about the “Cooling Rate – Time” curve as shown in figure (D).

• Time is plotted along X axis and cooling rate in terms of \left [ \log_e \left ( T - T_0 \right ) \right ] is plotted along Y axis.
• Clearly the relation is a straight line with negative slope.
• It indicates that rate of cooling decreases with pass of time.

Stefan Boltzmann Law of Cooling

Stefan Boltzmann law states that –

The total radiant heat power emitted from a hot surface is proportional to the fourth power of its absolute temperature.

Consider about a black body which is kept in an enclosure at temperature ( T_0 ) . Then –

• Rate at which the black body will absorb radiation from the enclosure is ( \sigma T^{4}_0 )
• Rate at which the black body emits radiation to enclosure is ( \sigma T^{4} )
• Therefore, the net loss of energy by the black body per unit time per unit area is \left [ E = \sigma \left ( T^4 - T^{4}_0 \right ) \right ]

If the body is not a black body, then the equation becomes –

\left ( \frac {dQ}{dt} \right ) = \epsilon \sigma \left ( T^4 - T^{4}_0 \right )

= e A \sigma \left ( T^4 - T^{4}_0 \right ) ……. (1)

From principle of calorimetry, rate of loss of energy by the body is –

\left ( \frac {dQ}{dt} \right ) = m c \left ( \frac {dT}{dt} \right ) …….. (2)

From equation (1) and (2) we have –

mc \left ( \frac {dT}{dt} \right ) = e A \sigma \left ( T^4 - T^{4}_0 \right )

Or, \quad \left ( \frac {dT}{dt} \right ) = \left ( \frac {eA \sigma}{mc} \right ) \left ( T^4 - T^{4}_0 \right ) ……… (3)

This equation gives cooling rate of a body.