What is called Flexural Rigidity?
Rigidity is the property of any material by virtue of which it offers resistance to deformation due to an applied load. A body having good rigidity will resist any type of deformation under the influence of load. Solid bodies are said to be rigid but, in reality they are not perfectly rigid. They can be stretched, compressed and bent. Flexural Rigidity is the term which determines the strength of any structural member.
Flexural rigidity is defined as the bending moment required to produce unit curvature in a beam. It gives the resistance offered by a structural member while undergoing bending moment. Flexural stiffness is the measure of ability of a member undergoing deformation
Therefore, flexural rigidity of a beam is defined as the product of modulus of elasticity for the material of beam and moment of inertia for the section of the beam. It is denoted by \left ( EI \right ) .
Importance of Flexural Rigidity
Flexural rigidity determines the strength of a beam. It is the main point of consideration by the engineers and designers while designing of a beam.
From differential equation of flexure, we have got the relation –
M = EI \left ( \frac {d^2y}{dx^2} \right )
In this expression, the product ( EI ) is known as flexural rigidity. It is a constant term in the differential equation of flexure.
Flexural rigidity depends upon the material of beam and type of cross section of beam.
Differential equation of flexure can also be expressed as –
M = \text {Flexural Rigidity} \ \times \ \left ( \frac {d^2y}{dx^2} \right )
Therefore, flexural rigidity –
- – gives the bending moment required to produce unit curvature in a beam.
- – gives the resistance offered by a structure while undergoing bending.
- – its stiffness is the measure of ability of a member undergoing deformation.
Unit of Flexural Rigidity
Flexural rigidity is the product of two quantities –
- Young’s modulus of elasticity or modulus of rigidity ( E ) for the material of beam. In SI system, its unit is [\text {N-m}^{-2} \text {or Pascal ( Pa )} ]
- Moment of inertia or second moment of area of cross section of the beam section ( I ) . In SI system, its unit is ( \text {m}^4 )
Therefore, unit of flexural rigidity will be –
\text {N-m}^{-2} \ \times \ \text {m}^4 = \text {N-m}^{2}
Deduction of Differential Equation of Flexure
An expression representing a relationship between moment of inertia ( I ) of a section of beam, elastic modulus ( E ) , bending moment ( M ) and differential operator \left ( \frac {d^2y}{dx^2} \right ) for elastic curve of a loaded beam is called differential equation of flexure.
This expression is given by –
M = EI \left ( \frac {d^2y}{dx^2} \right )
This equation is used to find slope and deflection of a beam by integration method popularly known as Double integration method.
Consider about a small portion PQ of a beam which has bent into an arc of a circle. Let –
- Length of beam portion PQ is ( ds )
- Centre of the arc of curvature of bent beam is ( C )
- Radius of curvature is ( R )
- Angle made by the tangent at point P with X axis is ( \psi )
- Angle made by tangent at point Q with X axis is ( \psi + d \psi )
- Co-ordinates of the point P are ( x, \ y )
- Co-ordinates of the point Q are [( x + dx ), \ ( y + dy )]
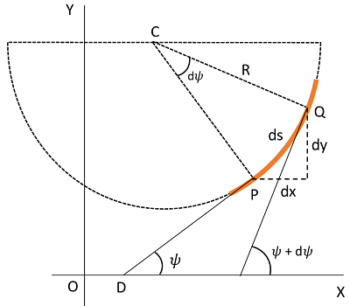
From geometry of the figure, we get –
\angle PCQ = d \psi
And length of arc PQ will be, \quad ds = R \ d \psi . Therefore, \quad R = \left ( \frac {ds}{d \psi} \right )
Since, bending is very small and points P and Q are very close, so we may assume ( ds = dx ) . Then –
\left ( \frac {ds}{d \psi} \right ) = \left ( \frac {dx}{d \psi} \right )
So, \quad R = \left ( \frac {dx}{d \psi} \right )
Or, \quad \left ( \frac {d \psi}{dx} \right ) = \left ( \frac {1}{R} \right )
An enlarged view of portion PQ of beam is shown in figure.
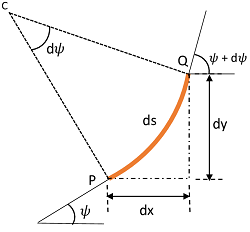
From geometry of the figure, we get –
\tan \psi = \left ( \frac {dy}{dx} \right )
Since, ( \psi ) is a very small angle, so –
\tan \psi = \psi ( in radians ).
- Therefore, \quad \psi = \left ( \frac {dy}{dx} \right )
Differentiating this expression with respect to ( x ) , we will get –
\frac {d}{dx} \left ( \psi \right ) = \frac {d}{dx} \left ( \frac {dy}{dx} \right )
= \left ( \frac {d^2y}{dx^2} \right )
But \quad \left ( \frac {d \psi}{dx} \right ) = \left ( \frac {1}{R} \right ) . Therefore, \quad \left ( \frac {1}{R} \right ) = \left ( \frac {d^2y}{dx^2} \right ) ……….. (6)
In article for bending stress, we have got the relation –
\left ( \frac {M}{I} \right ) = \left ( \frac {E}{R} \right )
= \left ( \frac {EI}{R} \right )
= EI \left ( \frac {1}{R} \right )
Using equation (6), we will get –
M = EI \left ( \frac {d^2y}{dx^2} \right ) ………. (7)
This expression is known as differential equation of flexure.
Methods to find Slope & Deflection
Many methods are available to determine the deflection and slope at a section of a loaded beam. The most important methods are –
- Double integration method.
- Moment area method.
- Macaulay’s method.
- Conjugate beam method.
In this article, we have discussed in detail for “Double integration method”. For other methods, we will discuss in detail on their respective articles.
Double Integration Method
Double integration method is used to find the slope and deflection at a point of a cantilever or a simply supported beam loaded with a single point load only.
In this method, we use differential equation of flexure, to find the slope and deflection by successive integration.
From differential equation of flexure, we have –
M = EI \left ( \frac {d^2y}{dx^2} \right ) …….. (7)
Integrating equation (7), we will get –
\int M = EI \left ( \frac {dy}{dx} \right ) + C_1 ………. (8)
Therefore, \quad \left ( \frac {dy}{dx} \right ) = \left ( \frac {1}{EI} \right ) \int M - C'_1 ……… (9)
Equation (9) gives slope, at any section of a beam.
Integrating equation (8) once again, we will get –
\iint M = EI \ y + C_2
Therefore, \quad y = \left ( \frac {1}{EI} \right ) \iint M - C'_2 ………… (10)
Equation (10) gives deflection at any section of a beam.
In equations (9) and (10) the values of integration constants ( C'_1 \ \& \ C'_2 ) are obtained from given end conditions of beam.
We will learn in detail about the procedure of application of “Double integration method” to find slope and deflection in beams in following numerical problems.
See numerical problems based on this article.
