Electric Field

What is called Electric Field of a Charge?

Electric field of a charged body is defined as the region or space around the body within which the influence of its static charge can be felt by another small test charge.

Every charged body produces its own field around itself.

Electric Field Intensity

The field intensity at a point in the electric field of a charged body is defined as the force experienced by a unit positive charge ( i.e. test charge ) placed at that point.

Let, a test charge $( q_0 )$ is placed at a point $P$ in the electric field of a source charge $( Q )$ . If, $( F )$ is the force experienced by the test charge in the field of the source charge, then field intensity at point $P$ will be –

$\vec {E} = \left ( \frac {F}{q_0} \right )$

Where, $( q_0 )$ is infinitesimally small so that, presence of this charge may not disturb the charge distribution of source charge $( Q )$ producing electric field.

Hence, field intensity can be written as –

$\vec {E} = \quad \lim\limits_{{ q_0} \longrightarrow 0 } \left ( \frac {F}{q_0} \right )$

Thus, electric force acting on a charge $( q )$ in the field $\vec {E}$ of a source charge $( Q )$ is given by –

$\vec {F} = q \vec {E}$

Electric field intensity is a vector quantity. Its direction is in the way in which a free unit positive charge tends to move in the electric field. The $SI$ unit of electric field intensity is newton per coulomb i.e. $N \ C^{-1}$

Electric Field by a Point Charge

Consider about a source charge $( Q )$ kept at point $A$ as shown in figure. This charge will create its own electric field $\vec {E}$ around itself.

To find the field intensity $\vec {E}$ at point $P$ at a distance $( r )$ from charge $( Q )$ , a test charge $( q_0 )$ is brought at point $P$ .

070301 ELECTRIC FIELD DUE TO A SINGLE CHARGE

Force experienced by the test charge at $P$ by the influence of electric field $\vec {E}$ of source charge $( Q )$ will be –

$\vec {F} = q_0 \vec {E}$

From Coulomb’s law, the electrostatic force on the test charge will be –

$\vec {F} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {Q q_0}{r^2} \right )$

Equating these forces, we will get –

$q_0 \vec {E} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {Q q_0}{r^2} \right )$

Therefore, electric field at point $P$ will be –

$\vec {E} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {Q}{r^2} \right )$

Principle of Superposition of Charges

The electric field at a point in space due to a set of charges may be obtained by finding the fields at that point due to each individual charge and then adding them according to the rules of vector addition. This is called principle of superposition of charges.

The principle of superposition of charges states that –

Net electric field strength at a point due to a set of charges is equal to the vector sum of all the electric field strengths produced due to individual charges at that point.

Electric Field by a Charged Ring

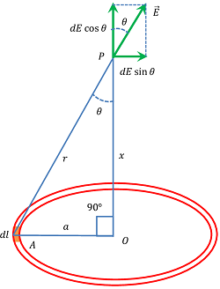
Consider about a uniformly charged thin ring as shown in figure. Let –

Radius of ring is $( a )$ .
$( \lambda )$ is the linear charge density on ring.
$P$ is a point on the axis of the ring at a distance $( x )$ from the centre of the ring.

Consider a small element of length $( dl )$ at distance $( r )$ from point $P$ . Charge on the element will be –

$dq = \lambda dl$ ……… (1)

Electric field intensity due to this element at point $P$ , will be –

$dE = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {dq}{r^2} \right )$

Using equation (1), we will get –

$dE = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {\lambda dl}{r^2} \right )$

Now, from right angled triangle $( \triangle {AOP} )$ we get –

$r^2 = ( x^2 + a^2 )$

Therefore, $\quad dE = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {\lambda dl}{(x^2 + a^2)} \right ]$ ………. (2)

Where $( dE )$ makes an angle $( \theta )$ with the axis of the ring. Resolving it into rectangular components we get –

Component $( dE \cos \theta )$ is acting parallel to the axis of the ring.
Component $( dE \sin \theta )$ is acting perpendicular to the axis of the ring.

The ring is considered to be consists of numerous such elements. Horizontal components $( dE \cos \theta )$ of all elements are added up as they are in the same direction. Perpendicular components $( dE \sin \theta )$ of one element is cancelled by $( dE \sin \theta )$ component of other element which is at just diametrically opposite of the ring.

In such a way, all perpendicular components will be cancelled out. Therefore, net electric field intensity will be –

$E = \sum {( dE \cos \theta )} = \int\limits_{ring} ( dE \cos \theta )$

Using equation (2), we will get –

$E = \int\limits_{ring} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {\lambda dl}{(x^2 + a^2)} \right ] \cos \theta$

Now, from $( \triangle {AOP} )$ we will get –

$\cos \theta = \left ( \frac {x}{r} \right ) = \left [ \frac {x}{(x^2 + a^2)^{\frac {1}{2}}} \right ]$

Therefore, $\quad E = \int\limits_{ring} \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {\lambda dl}{(x^2 + a^2)} \right ] \times \left [ \frac {x}{(x^2 + a^2)^{\frac {1}{2}}} \right ]$

Or, $\quad E = \left [ \frac {\lambda x}{4 \pi \epsilon_0 (x^2 + a^2)^{\frac {3}{2}}} \right ] \int\limits_{ring} dl$

But, $\quad \int\limits_{ring} dl = 2 \pi a =$ Circumference of the ring. Therefore, $\quad E = \left [ \frac {\lambda x}{4 \pi \epsilon_0 (x^2 + a^2)^{\frac {3}{2}}} \right ] \times 2 \pi a$

But, total charge on the ring $\quad Q = ( 2 \pi a ) \lambda$

Therefore, $\quad E = \left [ \frac {Q x}{4 \pi \epsilon_0 (x^2 + a^2)^{\frac {3}{2}}} \right ]$ ………. (3)

Direction of net field intensity is along the axis of the ring.

1. Field Intensity at infinite distance on axis of Charged Ring

Consider that the point $P$ is at an infinite distance on the axis of the charged ring. Then $( x >> a )$ . Therefore, $\quad ( x^2 + a^2 ) \cong x^2$ .

Putting this value in equation (3), we will get –

$E = \left ( \frac {Q}{4 \pi \epsilon_0 x^2} \right )$ . This will be acting along $OP$ .

This expression is the same as that of the electric field intensity at a distance $( x )$ from a single point charge $( Q )$ .

Thus ring behaves as a point charge kept at the centre of the ring if the point of observation is far away from the centre of the ring.

2. Field Intensity at centre of Charged ring

When point $P$ lies at the centre of the ring, then $( x = 0 )$ . Putting this value in equation (3) we will get –

$E = 0$ .

Thus electric field intensity at the centre of a charged ring is zero.

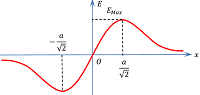
3. Maximum Field Intensity of Charged ring

For $( E )$ to be maximum $\left ( \frac {dE}{dx} \right )$ must be minimum.

But minimum value of $\left ( \frac {dE}{dx} \right ) = 0$

070303 MAXIMUM FIELD INTENSITY DUE TO A CHARGED RING

Therefore, $\quad \left ( \frac {d}{dx} \right ) \left [ \frac {Qx}{4 \pi \epsilon_0 ( x^2 + a^2 )^{\frac {3}{2}}} \right ] = 0$

Or, $\quad \left ( \frac {Q}{4 \pi \epsilon_0} \right ) \left ( \frac {d}{dx} \right ) \left [ \frac {x}{( x^2 + a^2 )^{\frac {3}{2}}} \right ] = 0$

Or, $\quad \left ( \frac {Q}{4 \pi \epsilon_0} \right ) \left [ \frac {- 3x^2}{( x^2 + a^2 )^{\frac {5}{2}}} + ( x^2 + a^2 )^{ (\frac {- 3}{2})} \right ] = 0$

Because $\left [ \left ( \frac {d}{dx} \right ) u^n = n \ u^{(n - 1)} \left ( \frac {du}{dx} \right ) \right ]$

By solving we will get –

$x = \pm \left ( \frac {a}{\sqrt {2}} \right )$

Thus electric field intensity due to a uniformly charged ring will be maximum at a distance of $\left ( x = \pm \frac {a}{\sqrt {2}} \right )$ from its centre on either side of the ring as shown in figure.

See numerical problems based on this article.