What is called Work?
Work is a form of energy. Work is said to be done by a force, if the force applied on a body resulting in the movement of body by some distance in the direction of applied force.
Therefore, for work done the following conditions must be fulfilled –
- A force acts on the body.
- The point of application of force on the body must have some displacement.
EXAMPLE –
- A man is trying to push a heavy load but fails to displace the load from its position. In this case, work is not being done, because point of application of force has no displacement.
- Another man is trying to pull the same load and in this case he succeeded in pulling it for some distance from its place. In this case work is being done, because point of application of force has some displacement.
Magnitude of Work
- The magnitude of work is given by the product of force and displacement.
Therefore, \quad \text {Work done} = \text {Force} \ \times \text {Displacement in the direction of force}
So, \quad W = ( F \times s )
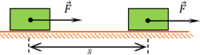
Consider about a block which is acted upon by a force ( F ) as shown in figure.
- In the figure, the force is acting horizontally.
- The point of application of force on the body moves through a distance ( s ) in the direction of application of force.

040501 WORK DONE BY A FORCE
Therefore, \quad W = F s
- Now let, the force is acting at an angle ( \theta ) from horizontal.
- The point of application of force on the body moves horizontally through a distance ( s ) as shown in figure.
Therefore, \quad W = \text {Component of force in the direction of displacement} \ \times \ \text {Displacement} .
Or, \quad W = ( F \cos \theta ) \times \ s = F s \cos \theta
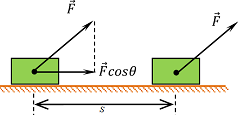
Also \quad F s \cos \theta = F \ \times \ ( s \cos \theta )
Therefore, \quad W = \text {Force} \ \times \ \text {Component of displacement in the direction of force} .
- Work is a scalar quantity and its magnitude may be positive, zero or negative.
Positive Work
If a force is acting on a body and the body moves in the direction of force, then the work done is positive.
Examples are –
- For a freely falling body, work done by gravity is positive.
- Work done by horse pulling a cart is positive.
- Work done by a stretched spring is positive.
Negative Work
If a force is acting on a body and the body moves in opposite to the direction of force, then the work done is negative.
Examples are –
- When a body slides on a rough horizontal plane, its displacement is opposite to the frictional force. Hence, work done by frictional force is negative.
- When braking of a car is done, the work done by braking force is negative.
- When a positive charge is moved towards another positive charge, work done by the force of repulsion is negative.
Zero Work
If a body gets displaced along a direction perpendicular to the direction of the applied force, then the work done is zero.
Also, the work done will be zero if either ( F = 0 ) or ( s = 0 ) .
Examples are –
- For a body moving in a circular path, work done by centripetal force is zero.
- In string of a simple pendulum, work done by the tension is zero.
- In pushing a immovable stone, the work done is zero.
Units of Work
In SI system, unit of work is ( \text {Joule} ) .
Joule
One joule of work is said to be done when a force of one newton displaces a body through a distance of one metre.
Therefore, \quad 1 \ \text {joule} = 1 \ \text {newton} \ \times \ \ 1 \ \text {metre} = 1 \ \text {N-m}
Erg
In CGS system, the unit of work is \text {erg} .
One erg of work is said to be done when a force of one dyne displaces a body through a distance of one centimetre.
Therefore, \quad 1 \ \text {erg} = 1 \ \text {dyne} \ \times \ 1 \ \text {cm}
Now, \quad 1 \ \text {joule} = 1 \ \text {newton} \ \times \ 1 \ \text {metre} = 10^5 \ \text {dyne} \ \times \ 10^2 \ \text {cm} = 10^7 \ \text {erg}
Work-Energy Theorem
Work energy theorem states that –
The work done by a force acting on a body is equal to the change in kinetic energy of that body.
1. Work-Energy Theorem for Constant Force
Consider that a constant force ( F ) is acting on a body of mass ( m ) which produces an acceleration ( a ) . This acceleration results in change of velocity from ( u ) to ( v ) .
- Then by Kinematic equations of motion, we have –
( v^2 - u^2 ) = 2as
Multiplying both sides by \left ( \frac {1}{2} m \right ) , we will get –
\left ( \frac {1}{2} m \right ) v^2 - \left ( \frac {1}{2} m\right ) u^2 = \left ( \frac {1}{2} m\right ) 2as
Or, \quad \left ( \frac {1}{2} \right ) m v^2 - \left ( \frac {1}{2} \right ) m u^2 = m a s
- But \quad \left ( \frac {1}{2} \right ) m u^2 is the initial kinetic energy ( K_i )
- And \quad \left ( \frac {1}{2} \right ) m v^2 is the final kinetic energy ( K_f )
Therefore, \quad ( K_f - K_i ) = m a s
- Also from Newton’s second law of motion, we have –
F = ma .
Therefore, \quad ( K_f - K_i ) = F \ s
Or, \quad ( K_f - K_i ) = W
Therefore, for a constant force, we have –
\text {Work done} = \text {Change in Kinetic Energy}
2. Work-Energy Theorem for Variable Force
Consider that a variable force ( \vec {F} ) is acting on a body of mass ( m ) which produces a displacement ( \vec {ds} ) . Let, the velocity of the body change from ( u ) to ( v ) .
- Then small work done –
dW = ( \vec {F} \times \vec {ds} ) = F ds
- According to Newton’s second law of motion, we have –
F = m a = \left [ m \left ( \frac {dv}{dt} \right ) \right ]
Therefore, \quad dW = \left [ m \left ( \frac {dv}{dt} \right ) \right ] ds = m \left ( \frac {ds}{dt} \right ) dv
But \left [ \left ( \frac {ds}{dt} \right ) = v \right ]
So, \quad dW = m v dv
- Therefore, total work done will be obtained by integration –
W = \int dW = \int\limits_{u}^{v} m v \ dv
= m \int\limits_{u}^{v} v \ dv
= m \left [ \frac {v^2}{2} \right ]_{u}^{v}
= \left ( \frac {1}{2} \right ) m v^2 - \left ( \frac {1}{2} \right ) m u^2
= ( K_f - K_i )
Therefore, for a variable force also we get –
\text {Work done} = \text {Change in Kinetic Energy}
See numerical problems based on this article.