What is Biot-savart Law?
If an electric current is passes through a conductor, it start to behave like a magnet. This means that, the current carrying conductor get magnetized due to current flowing through it. Using this property of a material, Biot-savart law states about the method of production of magnetic field by flow of a current through a conductor.
According to this law –
A magnetic field can be produced by a moving charges.
In other words, Biot-savart Law states that –
A magnetic field is produced by electric current flowing through a conductor.
Application of Biot-savart Law
Biot-savart law is very useful in finding the magnetic field in following cases –
- Magnetic field intensity developed by a current carrying wire of infinite length.
- Field intensity by a current wire of definite length.
- Magnetic field intensity developed by a circular loop at any point on its axis.
- Field intensity of a coil at any point on its axis.
- Magnetic field at centre of an arc etc.
Equation of a Biot-savart Law
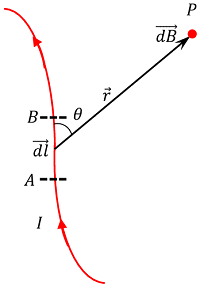
Consider about a point P near a current carrying conductor as shown in figure. Let –
- AB is a very small element of length ( dl ) of the conductor.
- Current in the conductor is ( I ) .
- Distance of point P from the centre of element is ( r ) .
- At point P , the intensity of magnetic field due to current in the element is ( dB ) .
- Angle between ( \vec {dl} ) and ( \vec {r} ) is ( \theta ) .

091201 BIOT-SAVART LAW OF MAGNETIC FIELD
According to Biot – savart law, the strength of magnetic field ( dB ) at a point P will be –
- Proportional to the length of current element i.e. ( dB \propto dl )
- Inversely proportional to the square of the distance of point P from the current element i.e. \left [ dB \propto \left ( \frac {1}{r^2} \right ) \right ]
- Proportional to the magnitude of current in the element i.e. ( dB \propto I )
- Depends upon the angle between flow of current and radial distance i.e. ( dB \propto \sin \theta ) .
Combining all of the above relations, we will get –
dB \propto \left ( \frac {I dl \sin \theta }{r^2} \right )
= k \left ( \frac {I dl \sin \theta }{r^2} \right ) .
Here, ( k ) is a constant of proportionality. This constant depends upon absolute permeability of free space ( \mu _0 ) .
k = \left ( \frac {\mu_0}{4 \pi} \right )
In SI system, its value is ( 10^{-7} \ \text {weber per ampere-metre} ) \ \text {or} \ ( 10^{-7} \ \text {tesla-meter per ampere} )
Therefore, \quad dB = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I dl \sin \theta }{r^2} \right ) …….. (1)
In vector form, the magnetic field at point P is given by –
d \vec {B} = \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {I \left ( \vec {dl} \times \vec {r} \right ) }{r^3} \right ] …….. (2)
Direction of ( d \vec {B} ) is same as that of cross product ( d \vec {l} ) \times ( \vec {r} ) . This direction can also be obtained from Right hand screw rule or Right hand thumb rule.
The net magnetic field at point P due to the whole conductor is now obtained by integrating equation (2).
Magnetic Field produced by a straight wire
Consider about a long straight wire AB carrying a current ( I ) as shown in figure. Now consider about a point P at a distance ( x ) from the wire.
Consider a small current element of length ( dl ) at a distance ( l ) from the centre O of the wire. Let, ( r ) is the distance of point P from the current element ( dl ) .
According to Biot-savart law, magnetic field at point P due to the small current element ( dl ) will be –
dB = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I dl \sin \phi }{r^2} \right ) ……….. (1)
From right angled triangle \triangle POC , we will get –
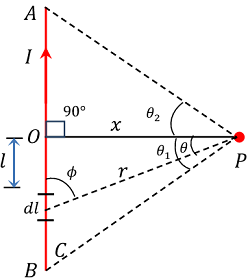
\sin \phi = \left ( \frac {x}{r} \right ) = \cos \theta ………. (2)
So, \quad r = \left ( \frac {x}{\cos \theta } \right ) ………. (3)
Also, \quad \tan \theta = \left ( \frac {l}{x} \right )
Or, \quad l = x \tan \theta
Since, ( x ) is fixed, so differentiating above equation, we will get –
dl = x \ {\sec}^2 \ \theta \ d \theta ………. (4)
Now, substituting the values from equations (2), (3) and (4) in equation (1), we will get –
dB = \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {I \left ( x \sec^2 \theta d \theta \right ) \cos \theta }{ \left ( x^2 / \cos^2 \theta \right) } \right ]
= \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {I \left ( x \sec^2 \theta d \theta \right ) \cos \theta }{ \left ( x^2 \sec^2 \theta \right) } \right ]
= \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I \cos \theta d \theta }{ x } \right ) ………. (5)
Magnetic field due to whole conductor AB is then calculated by integrating the equation (5) within the limits of \left ( - \theta _1 \right ) and \left ( + \theta _2 \right )
Therefore, \quad B = \int\limits_{- \theta _1}^{\theta _2} dB = \left ( \frac {\mu _0 I}{4 \pi x} \right ) \int\limits_{- \theta _1}^{\theta _2} \cos \theta d \theta
= \left ( \frac {\mu _0 I}{4 \pi x} \right ) \left [ \sin \theta \right ] _ {- \theta _1}^{\theta _2} = \left ( \frac {\mu _0 I}{4 \pi x} \right ) \left [ \sin \theta _2 - \sin \left ( -\theta _1 \right ) \right ]
= \left ( \frac {\mu _0 I}{4 \pi x} \right ) \left [ \sin \theta _1 + \sin \theta _2 \right ] ……….. (6)
This is the general equation to find magnetic field by a straight conductor carrying a current. Two different situations are possible –
- The conductor is of infinite length.
- The conductor is of finite length.
1.Magnetic field of an infinite long wire
A infinitely long wire means a wire of very large length. For an infinitely long wire, we have –
\theta _1 = \theta _2 = \left ( \frac {\pi}{2} \right )
Then equation (6) becomes –
B = \left ( \frac {\mu _0 I}{4 \pi x} \right ) \left [ \sin \frac {\pi}{2} + \sin \frac {\pi}{2} \right ] = 2 \left ( \frac {\mu _0 I}{4 \pi x} \right )
= \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {2 I}{x} \right ] ……….. (7)
2.Magnetic field of a finite long wire
A finite long wire means a wire of short length. For a finite long wire we have –
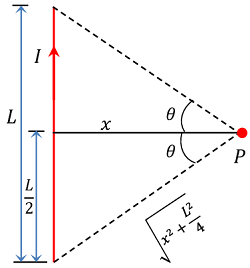
\theta _1 = \theta _2 = \theta (say)
Consider about a conductor of finite length as shown in figure. By geometry of the figure –
\sin \theta = \left ( \frac {L / 2}{\sqrt {x^2 + L^2 / 4}} \right ) = \left ( \frac {L}{\sqrt {L^2 + 4 x^2}} \right )
Hence, equation (6) becomes –
B = \left ( \frac {\mu _0 I}{4 \pi x} \right ) \times \left ( \frac {2 L}{\sqrt {L^2 + 4 x^2}} \right )
= \left (\frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 I L}{x \sqrt {L^2 + 4 x^2}} \right ) ………. (8)
See numerical problems based on this article.