Combination of Cells

How combination of cells are done?

Sometimes a combination of cells are used in a circuit to get the desired EMF which is not possible by a single cell. These cells are connected in different combinations as –

Identical cells of same EMF connected in series.
Different cells of different EMF connected in series.
Identical cells of same EMF connected in parallel.
Different cells of different EMF connected in parallel.

Combination of identical cells in Series

In series combination of cells the negative terminal of one cell is connected with the positive terminal of the next cell and so on.

Consider that $( n )$ identical cells $( C_1 ), \ ( C_2 ), \ ........... \ ( C_n )$ etc. each of EMF $( E )$ and internal resistance $( r )$ are connected in series to an external resistance $( R )$ .

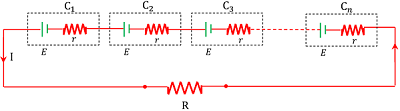
080701 SERIES COMBINATION OF IDENTICAL CELLS

Since, cells are connected in series. So, the total EMF of combination of cells will be –

$E_{eff} = n E$

Also, all the internal resistances of the cells are in series.

Therefore, effective internal resistance of the circuit will be –

$r_{eff} = nr$

This in turn is connected in series with the external resistance $( R )$ .

Therefore, equivalent resistance of circuit will be –

$R_{eq} = ( R + nr )$

Therefore, current flowing through the circuit will be –

$I = \left ( \frac {\text {Effective emf}}{\text {Equivalent resistance}} \right ) = \left ( \frac { nE }{ R + nr } \right )$ …….. (1)

Thus, combination of cells in series should be used after considering about two points as mentioned below –

External resistance is very large as compared to the internal resistance of cell.
External resistance is too small as compared to the internal resistance of cell.

1. When external Resistance is very large

When the external resistance in the circuit is very large such that $( R >> nr )$

Then, $\quad ( R + nr ) \cong R$

Hence, equation (1) becomes –

$I = \left ( \frac { nE }{ R } \right ) = n \left ( \frac { E }{ R } \right )$

But, $\left ( \frac { E }{ R } \right )$ is the current supplied by one cell.

Therefore, it is useful to use a combination of cells connected in series to increase current in a circuit having very large external resistance as compared to internal resistance of cells. The total current flowing in the circuit becomes $( n )$ times of the current supplied by one cell.

2. When external Resistance is very small

When external resistance is very small such that $( R << n r )$

Then, $( R + nr ) \cong n r$

Hence, equation (1) becomes –

$I = \left ( \frac { nE }{ nr } \right ) = \left ( \frac { E }{ r } \right )$ which is equal to the current supplied by one cell.

Therefore, when a large number of cells are connected to a very small external resistance, then total current flowing in the circuit will be the same as that of current supplied by one cell.

Therefore, it is use less to use a combination of cells connected in series to increase the current in a circuit having very small external resistance as compared to the internal resistance of cells.

Hence, combination of cells in series is of importance, only if the external resistance in the circuit is very large as compared to total internal resistance of a cells i.e. when $( R >> r )$

Combination of different cells in Series

Consider two cells of EMF $( E_1 ), \ ( E_2 )$ and internal resistances of $( r_1 ), \ ( r_2 )$ respectively are connected in series.

Since, cells are connected in series so the total EMF of combination of cells will be –

$E_{eff} = ( E_1 + E_2 )$

Also, the internal resistance of the cells are in series. So, the total internal resistance is –

$r_{ eq } = ( r_1 + r_2 )$ .

Then, current flowing through the circuit will be –

$I = \left ( \frac { E_{ eff }}{ r_{ eq }} \right ) = \left ( \frac { E_1 + E_2 }{ r_1 + r_2 } \right )$ ……… (2)

Combination of identical cells in Parallel

In a parallel combination of cells, negative terminals of all cells are connected together and in the same way all the positive terminals are connected together.

A parallel combination of cells is shown in figure.

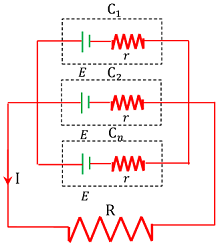
080702 PARALLEL COMBINATION OF IDENTICAL CELLS

Consider $( n )$ number of identical cells $( C_1 ), \ ( C_2 ), \ ........... \ ( C_n )$ , each of EMF $( E )$ and internal resistance $( r )$ , are connected in parallel to an external resistance $( R )$ .

Since, cells are connected in parallel so the total EMF of combination of cells will be –

$E_{eff} = E$

All the internal resistances of the cells are connected in parallel with each other. So, their effective internal resistance $( r_{eff} )$ is obtained as –

$\left ( \frac { 1 }{ r_{eff} } \right ) = \left [ \frac { 1 }{ r } + \frac { 1 }{ r } + \frac { 1 }{ r } + ........ \right ] = \left ( \frac { n }{ r } \right )$

Therefore, effective internal resistance is –

$r_{eff} = \left ( \frac { r }{ n } \right )$

Also, effective resistance $( r_{eff} )$ and external resistance $( R )$ are connected in series.

Therefore, equivalent resistance of the circuit is –

$R_{eq} = ( R + r_{eff} ) = \left ( R + \frac { r }{ n } \right )$

Then, current flowing through the circuit will be –

$I = \left ( \frac {\text {Effective emf}}{\text {Equivalent resistance}} \right ) = \left [ \frac { E }{ \left ( R + \frac { r }{ n } \right ) } \right ] = \left ( \frac { n E }{ nR + r } \right )$ ………. (3)

Thus, combination of cells in parallel should be used after considering about two points as mentioned below –

External resistance is very large as compared to the internal resistance of cell.
External resistance is too small as compared to the internal resistance of cell.

1. When external Resistance is very large

When external resistance is very large such that $( R >> r )$ . Then –

$( nR + r ) \cong nR$

Hence, equation (3) becomes –

$I = \left ( \frac { nE }{ nR + r } \right ) = \left ( \frac { nE }{ nR } \right ) = \left ( \frac { E }{ R } \right )$

But, $\left ( \frac { E }{ R } \right )$ is the current supplied by one cell.

Therefore, it is use less to use a combination of cells connected in parallel to increase the current in a circuit having very large external resistance as compared to the internal resistance of cells.

2. When external Resistance is very small

When external resistance is very small such that $( R << r )$

Then $( nR + r ) \cong r$

Hence, equation (3) becomes –

$I = \left ( \frac { nE }{ nR + r } \right ) = \left ( \frac { nE }{ r } \right ) = n \left ( \frac { E }{ r } \right )$ .

But, $\quad \left ( \frac { E }{ r } \right )$ is equal to the current supplied by one cell.

Therefore, it is useful to use a combination of cells connected in parallel to increase current in a circuit having small external resistance compared to internal resistance of cells. The total current flowing in the circuit becomes $( n )$ times of the current supplied by one cell.

Hence, combination of cells in parallel is of importance, only if the external resistance in the circuit is very small as compared to internal resistance of a cell i.e. when $( R << r )$

Combination of different cells in Parallel

Consider two cells of EMF $( E_1 ), \ ( E_2 )$ and internal resistances $( r_1 ), \ ( r_2 )$ respectively are connected in parallel.

If $( I_1 )$ and $( I_2 )$ are the currents supplied by individual cells then total current in the main circuit will be –

$I = ( I_1 + I_2 )$ ………. (a)

Since, cells are connected in parallel so the terminal potential difference of combination of cells will be the same. Let it is $( V )$ . Then –

For the first cell $\quad V = ( E_1 - I_1 r_1 )$

Or, $\quad I_1 = \left ( \frac {E_1 - V}{ r_1 } \right )$

Similarly for the second cell $\quad V = ( E_2 - I_2 r_2 )$

Or, $\quad I_2 = \left ( \frac {E_2 - V}{ r_2 } \right )$

Putting the values of $( I_1 )$ and $( I_2 )$ in equation (a) we get –

$I = \left [ \left ( \frac {E_1 - V}{ r_1} \right ) + \left ( \frac {E_2 - V}{ r_2} \right ) \right ]$

Or, $\quad I = \left ( \frac {E_1 r_2 + E_2 r_1}{ r_1 r_2} \right ) - V \left ( \frac { r_1 + r_2 }{ r_1 r_2} \right )$

Therefore, $\quad V = \left ( \frac {E_1 r_2 + E_2 r_1 }{ r_1 + r_2 } \right ) - I \left ( \frac { r_1 r_2 }{ r_1 + r_2} \right )$ ………. (b)

Let, the parallel grouping of cells is replaced by a single cell of equivalent emf $( E_{ eq } )$ and internal resistance $( r_{ eq } )$ then –

$V = ( E_{ eq } - I r_{ eq } )$ ……… (c)

By comparing equations (b) and (c) we get –

$E_{ eq } = \left ( \frac {E_1 r_2 + E_2 r_1 }{ r_1 + r_2 } \right )$

And $\quad r_{ eq } = \left ( \frac { r_1 r_2 }{ r_1 + r_2} \right )$

Therefore, $\left ( \frac { E_{ eq}}{ r_{ eq }} \right ) = \left ( \frac {E_1 r_2 + E_2 r_1 }{ r_1 r_2 } \right ) = \left ( \frac { E_1 }{ r_1 } + \frac { E_2 }{ r_2} \right )$

Or, $\quad E_{ eq} = \left [ \frac { E_1 }{ r_1 } + \frac { E_2 }{ r_2} \right ] r_{ eq }$ ………. (4)

See numerical problems based on this article.