Magnetic Field by Circular loop carrying current
Magnetic field produced by a circular loop carrying a current is obtained by the application of Biot-savart law.
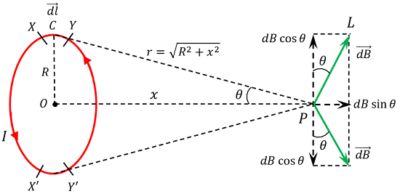
Consider about a point P on the axis of a circular loop carrying a current as shown in figure. Let –
- XY is a very small element of length ( dl ) of the loop.
- Current in the circular loop is ( I ) .
- Radius of the circular loop is ( R ) .
- Distance of point P from the centre of circular loop is ( x ) .
- Distance of point P from the centre of element XY is ( r ) .
- At point P , the intensity of magnetic field due to current in the loop is ( dB ) .
- Angle between ( \vec {dl} ) and ( \vec {r} ) is ( \phi ) .
Equation for Magnetic Field of circular loop
According to Biot-savart law, the strength of magnetic field ( dB ) at a point P will be –
- Proportional to the length of current element i.e. ( dB \propto dl )
- Inversely proportional to the square of the distance of point P from the current element i.e. \left [ dB \propto \left ( \frac {1}{r^2} \right ) \right ]
- Proportional to the magnitude of current in the element i.e. ( dB \propto I )
- Depends upon the angle between flow of current and radial distance i.e. ( dB \propto \sin \phi ) .
Every current element is perpendicular to ( \vec {r} ) i.e. the direction of ( r ) as shown in figure.
Therefore, \quad \phi = 90 \degree
Or, \quad \sin \phi = \sin 90 \degree = 1 .
According to Biot-savart law, magnetic field at point P due to small element XY , will be –
dB = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I dl \sin \phi }{r^2} \right ) ……. (1)
Since, for the circular loop ( \sin \phi = 1 ) , we get –
dB = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I dl}{r^2} \right ) ……….. (2)
The direction of ( \vec {dB} ) is obtained from Right hand screw rule or Right hand thumb rule. It is perpendicular to the plane formed by ( \vec {dl} ) and ( \vec {r} ) and is along PL which is perpendicular to PC as shown in figure.
Resolving ( dB ) into rectangular components, we get –
- Component ( dB \cos \theta ) is perpendicular to the axis of the loop.
- Component ( dB \sin \theta ) is along the axis of the loop and away from the centre of loop.
As the loop is symmetrical about its axis, so every current element of length ( dl ) has another equal and opposite element on the circular loop.
For example –
Current element XY has equal and opposite current element X'Y' . The perpendicular components of the magnetic field due to these current elements being equal and opposite, they will cancel to each other. Hence, the total contribution of perpendicular components of the magnetic field is zero.
Also, ( dB \sin \theta ) component of magnetic field due to each current element of the loop is directed in the same direction. So, magnetic field at point P due to the whole current carrying loop is equal to the sum of ( dB \sin \theta ) components of magnetic field of all current elements.
Therefore, \quad B = \Sigma ( dB \sin \theta )
= \int ( dB \sin \theta )
Using equation (2), we will get –
B = \int \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I dl}{r^2} \right ) \sin \theta
= \left ( \frac {\mu _0 I \sin \theta}{4 \pi r^2} \right ) \int dl
= \left ( \frac {\mu _0 I }{4 \pi r^2} \right ) \sin \theta \int dl ……… (3)
But, \left [ \int dl = ( 2 \pi R ) \right ] ( Circumference of the loop )
And, \left [ \sin \theta = \left ( \frac {R}{r} \right ) \right ]
Putting these values in equation (3), we get –
B = \left ( \frac {\mu _0 I}{4 \pi r^2} \right ) \left ( \frac {R}{r} \right ) \left ( 2 \pi R \right )
= \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 \pi I R^2}{r^3} \right )
Also, \quad r = \left ( \sqrt {R^2 + x^2} \right ) = \left [ \left ( R^2 + x^2 \right )^{\frac {1}{2}} \right ]
Therefore, \quad B = \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {2 \pi I R^2}{\left ( R^2 + x^2 \right )^{(3/2)}} \right ] ………… (4)
Magnetic Field at a point on axis of a Coil
Magnetic field at a distance ( x ) from centre of a loop on the axis is given by the equation –
B = \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {2 \pi I R^2}{\left ( R^2 + x^2 \right )^{(3/2)}} \right ] ………… (4)
Now, consider a coil having ( N ) number of turns.
Then magnetic field at a distance ( x ) from the centre of coil on its axis will be –
B' = \left ( \frac {\mu _0}{4 \pi} \right ) \left [ \frac {2 \pi N I R^2}{\left ( R^2 + x^2 \right )^{(3/2)}} \right ] …………. (5)
Magnetic Field at infinity from the centre of loop
Consider about a point P which is at infinite distance from centre of the loop. Then ( x >> R ) and so the term ( R^2 ) in equation (4) can be neglected.
Hence, \left ( R^2 + x^2 \right )^{3/2} \cong ( x )^3
Therefore, for magnetic field at infinity, the equation (4) becomes –
B = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 \pi I R^2}{x^3} \right )
= \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 I A}{x^3} \right ) …………. (6)
Here, ( \pi R^2 ) = A \ \text {( Area of the loop )}
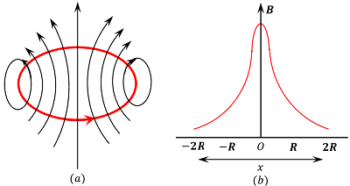
- Magnetic field lines of a current carrying circular loop or coil are shown in figure ( a ).
- Variation of magnetic field of a current carrying loop along its axis is shown in figure ( b ).
- Magnetic field intensity is maximum at the centre of the loop and it decreases exponentially with increase in distance from centre.
Magnetic Field at centre of loop
At the centre of loop ( x = 0 ) . Hence, from equation (4), we will get –
B = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 \pi I R^2}{R^3} \right )
= \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 \pi I}{R} \right ) …………. (7)
If a coil consists of ( N ) number of turns, then magnetic field due to the current carrying coil at its centre will be –
B = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {2 \pi N I}{R} \right ) ……….. (8)
- Direction of magnetic field is obtained from the Right hand screw rule or Right hand thumb rule.
- When the current flows in clockwise direction in the loop or coil, the direction of magnetic field at the centre is perpendicular to the plane of loop and in the downward direction.
- When the current flows in anti clockwise direction in the loop or coil, the direction of magnetic field at the centre is perpendicular to the plane of loop and in the upward direction.
Magnetic Field of an arc at centre
Consider about a current carrying wire of circular arc which subtends an angle ( \theta ) in radian at its centre as shown in figure.
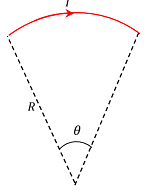
We know that, a complete circle subtends an angle ( 2 \pi ) in radians at its centre. Hence, magnetic field at the centre of circular loop due to an arc subtending unit radian angle will be –
B'' = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I}{R} \right ) \times \left ( \frac {1}{2 \pi} \right )
Therefore, magnetic field due to current carrying circular arc subtending an angle ( \theta ) in radian at its centre will be –
B = \left ( \frac {\mu _0}{4 \pi} \right ) \left ( \frac {I}{R} \right ) \times \left ( \frac {\theta}{2 \pi} \right )
See numerical problems based on this article.
