What are called Displacement and Velocity?
Displacement of any moving body is defined as the vector difference between the end and start position vectors of the body. It is different from the actual distance travelled by that moving body along the way. Velocity is the rate at which displacement changes with time.
Velocity
Velocity of a moving body is defined as the rate of change of position of body i.e. rate of displacement.
If, ( s ) is the displacement done by a moving body in a time span of ( t ) , then velocity is expressed mathematically in the form as \quad v = \left ( \frac {\Delta s}{\Delta t} \right )
Displacement
Displacement of body is the vector difference of the end and start position vectors of the body in the time span under consideration.
Therefore, displacement is defined as the change in position of an object in a given direction in a given time.
- Since, direction is considered, so velocity and displacement both are vector quantities.
- Displacement is the shortest distance between start point and end point of a journey.
Distance
Distance is defined as the actual length of path traveled by a moving body without specifying the direction of movement.
Since, direction is not considered, so distance is a scalar quantity.
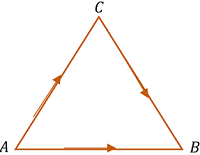
Consider that a body moves from point A to point B . The path of travel is from starting point A then to a mid point C and then from point C to end point B . Path of travel is shown in figure.
Thus, distance traveled by body will be ( AC + CB ) and displacement will be ( AB )
TO BE NOTED –
Physical quantities are of two types –
- Scalar Quantity – A scalar quantity is that quantity which has only magnitude. Example – Distance, time, density, specific heat etc.
- Vector Quantity – A vector quantity has magnitude and direction both. To specify a vector quantity magnitude and direction both are stated. Example – Displacement, velocity, acceleration, weight etc.
Difference between Distance and Displacement
The basic differences between distance and displacement of a body are as follows –
| Points | Distance | Displacement |
| Magnitude. | It is the total length of actual path traveled between start point and end point. | It is the shortest distance between start point and end point. |
| Route. | It is measured along the actual path traveled by object. | It is measured directly between start point and end point. Actual path of travel is insignificant. |
| Quantity. | It has only magnitude. It is a scalar quantity. | It has magnitude and direction both. It is a vector quantity. |
| Direction. | It has no direction. | It has specified direction. |
| Values. | Its value may be positive or zero but never be negative. | Its value may be positive, zero or even negative. |
| Comparison. | Its value is either equal to or greater than displacement. | Its value is either equal to or less than distance but never be greater than distance. |
Different types of Speed
Speed of a moving body is defined as the rate of change of its position with respect to time.
Therefore, \quad \text {Speed} = \left ( \frac {\text {Total distance traveled}}{\text {Total time}} \right )
The SI unit of speed is ( m \ s^{-1} )
Different types of speeds are –
- Uniform speed.
- Variable speed.
- Average speed.
- Instantaneous speed.
1. Uniform Speed
When a moving body covers equal distances in equal intervals of time, then its speed is said to be uniform speed.
Consider that a body covers a distance of ( s_1 ) \ \text {and} \ ( s_2 ) in time intervals of ( t_1 ) \ \text {and} \ ( t_2 ) respectively.
Then, for uniform speed –
\left ( \frac {s_1}{t_1} \right ) = \left ( \frac {s_2}{t_2} \right )
2. Variable Speed
When a moving body covers different distances in equal intervals of time, then its speed is said to be non-uniform speed or variable speed.
Consider that a body covers distances of ( s_1 ) \ \text {and} \ ( s_2 ) in time intervals of ( t_1 ) \ \text {and} \ ( t_2 ) respectively.
Then, for non-uniform or variable speed –
\left ( \frac {s_1}{t_1} \right ) \ \neq \ \left ( \frac {s_2}{t_2} \right )
3. Average Speed
The speed of a moving body can change several times during the entire journey due to acceleration, breaking, stalling etc. Hence, concept of average speed is of significant for long journey.
Average speed of a moving body is defined as the total distance traveled per unit time.
Therefore, average speed –
\bar {v} = \left ( \frac {\text {Total distance traveled}}{\text {Total time taken}} \right )
4. Instantaneous Speed
The speed of an object at any particular instant of time or at a particular point of its path is called the instantaneous speed.
Consider about a body which covers a distance ( \Delta x ) in a small time interval ( \Delta t ) around time instant ( t ) . Then it’s average speed is \left ( \frac {\Delta x}{\Delta t} \right ) .
The limiting value of this average speed, when time interval ( \Delta t ) approaches to zero, gives the instantaneous speed.
Thus, instantaneous speed –
v = \lim\limits_{\Delta t \rightarrow 0} \frac {\Delta x}{\Delta t} = \left ( \frac {dx}{dt} \right )
Hence, speed is the first order derivative of distance ( x ) with respect to time ( t ) .
Different types of Velocity
Velocity of a moving body is defined as the rate of change of position of body with respect to time in a particular direction.
It is equal to the displacement in unit time.
Therefore, \quad \text {Velocity} = \left ( \frac {\text {Displacement}}{\text {Total time}} \right )
In calculus method, velocity is defined as \left [ v = \left ( \frac {ds}{dt} \right ) \right ] Where ( s ) represents the displacement.
The SI unit of velocity is ( m \ s^{-1} )
Different types of velocities are –
- Uniform velocity.
- Variable velocity.
- Average velocity.
- Instantaneous velocity.
1. Uniform Velocity
When a moving body covers equal displacements in equal intervals of time, then its velocity is said to be uniform velocity.
Consider that a body covers a displacements of ( s_1 ) \ \text {and} \ ( s_2 ) in time intervals of ( t_1 ) \ \text {and} \ ( t_2 ) respectively.
Then, for uniform velocity –
\left ( \frac {s_1}{t_1} \right ) = \left ( \frac {s_2}{t_2} \right )
2. Variable Velocity
When a moving body covers different displacements in equal intervals of time, then its velocity is said to be non-uniform or variable velocity.
Consider that a body covers a displacements of ( s_1 ) \ \text {and} \ ( s_2 ) in time intervals of ( t_1 ) \ \text {and} \ ( t_2 ) respectively.
Then for non-uniform or variable velocity –
\left ( \frac {s_1}{t_1} \right ) \ \neq \ \left ( \frac {s_2}{t_2} \right )
3. Average Velocity
The velocity of a moving body can change several times during the entire journey due to acceleration, breaking, stalling etc. Hence, concept of average velocity is of significant for long journey.
Average velocity of a moving body is defined as the ratio of total displacement to total time interval.
Therefore, average velocity –
\bar {v} = \left ( \frac {\text {Total displacement}}{{Total time taken}} \right )
If ( x_1 ) \ \text {and} \ ( x_2 ) are the positions of an object at time ( t_1 ) \ \text {and} \ ( t_2 ) respectively, then the average velocity from time ( t_1 ) \ \text {to} \ ( t_2 ) is given by –
v_{av} = \left [ \frac {x_2 - x_1}{t_2 - t_1} \right ] = \frac {\Delta x}{\Delta t}
4. Instantaneous Velocity
The velocity of an object at any particular instant of time or at a particular point of its path is called the instantaneous velocity.
It is equal to the limiting value of the average velocity of object in small time interval ( \Delta t ) , when the time interval approaches to zero.
Thus, Instantaneous velocity –
\vec v = \lim\limits_{\Delta t \rightarrow 0} \frac {\Delta \vec x}{\Delta t} = \left ( \frac {d \vec x}{dt} \right )
Hence, Instantaneous velocity of an object is the first order derivative of displacement ( \vec x ) with respect to time ( t ) .
Difference between Speed & Velocity
The basic differences between speed and velocity of a moving body are as follows –
| Points | Speed | Velocity |
| Magnitude. | It is the distance covered per unit time. | It is the displacement covered per unit time. |
| Quantity. | It has only magnitude. So, it is a scalar quantity. | It has magnitude and direction both. So, it is a vector quantity. |
| Direction. | It has no direction. | It has specified direction. |
| Values. | Its value may be positive or zero. | Its value may be positive, zero or negative. |
| Comparison. | Its value is either equal to or greater than velocity. | Its value is either equal to or less than speed but never be greater than speed. |
See numerical problems based on this article.
