Charge Motion in Magnetic Field

What happen when a charge moves in a Magnetic Field?

When a charge is projected to move in a magnetic field, it experiences a force on it. Hence, a charge moving in a magnetic field experience Lorentz force.

The projected charged particle while moving through the region of magnetic field, gets deflected from its original path of motion die to force. The trajectory of the path of motion depends upon the direction of projection of the charge in the magnetic field. The motion of particle in the magnetic field will be influenced by the Lorentz force.

From Lorentz force, magnetic force on a charge ( q ) moving with velocity ( v ) at an angle ( \theta ) with the direction of magnetic field ( \vec {B} ) , is given by –

\vec {F_m} = q \left ( \vec {v} \ \times \ \vec {B} \right ) ( In vector form. )

Or, \quad F_m = q \ ( v \ B \ \sin \theta ) ( In analytical form. )

A charged particle may be projected to enter in the region of magnetic field in three different ways as follows –

1. Particle enters in the magnetic field in a direction parallel to the direction of magnetic field.
2. It enters in the magnetic field in a direction perpendicular to the direction of magnetic field.
3. Particle enters in the magnetic field at an angle to the direction of magnetic field.

1. Charge moving parallel to the direction of Magnetic Field

When a charge enters the magnetic field in parallel or anti-parallel direction to the direction of magnetic field, then ( \theta = 0 \degree \ \text {or} \ 180 \degree )

Therefore, \quad \sin \theta = 0

• Hence, the moving charge will experience no magnetic force.
• The charge will continue to move in projected direction of motion.

2. Charge moving perpendicular to the direction of Magnetic Field

When a charged particle enters in magnetic field in direction perpendicular to the direction of the field, then ( \theta = 90 \degree )

Therefore, \quad \sin \theta = 1

• Hence, the particle will experience a magnetic force and deviate from its original path.
• The particle will follow to move in a circular path.

Consider about a charged particle entering in a magnetic field. Let –

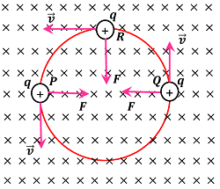
• Charge on particle is (+ q) .
• Initial velocity of projection is ( \vec {v} ) .
• Direction of projection is at right angle to the direction of magnetic field ( \vec {B} ) as shown in figure.

Then, magnetic force on the charge will be –

F = q v B \sin \theta = q v B \sin 90 \degree = q v B ……… (1)

By Fleming’s left hand rule, the direction of magnetic force is always (1) perpendicular to the direction of motion of the particle (2) perpendicular to the direction of magnetic field.

Thus, the path of the charged particle is circular in a plane which is perpendicular to the plane containing ( \vec {v} \ \text {and} \ \vec {B} ) as shown in figure.

Radius of circular path

Consider that –

• Mass of the charged particle is ( m ) and
• Radius of circular path of particle is ( r ) .

Then, necessary centripetal force on particle will be provided by Lorentz force. Therefore –

\left ( \frac {mv^2}{r} \right ) = q v B

So, \quad r = \left ( \frac {mv^2}{q V B} \right )

= \left ( \frac {m v}{q B} \right )

= \left [ \frac {v}{( q / m ) B} \right ] ……….. (2)

= \left [ \frac {v}{q_s \ B} \right ]

Here, \left [ \left ( \frac {q}{m} \right ) = q_s \right ] is the charge per unit mass of the particle. It is called specific charge.

Time period of circular motion

Time to complete one cycle by the charged particle will be –

T = \left ( \frac {\text {Distance}}{\text {Speed}} \right )

= \left ( \frac {2 \pi r}{v} \right )

Putting the value of ( r ) from equation (2), we get –

T = \left ( \frac {2 \pi m}{q B} \right ) ……. (3)

Frequency of motion

Frequency of a circular motion is given by –

\nu = \left ( \frac {1}{T} \right )

Hence, frequency of circular motion of the charged particle will be –

\nu = \left ( \frac {q B}{2 \pi m } \right ) ……… (4)

From equations (3) and (4), we find that, the time period and frequency of motions are –

1. Independent of projected speed ( v ) of particle.
2. Not depends on radius ( r ) of the circular path.
3. Depends on the magnetic field B .
4. Depends on specific charge \left [ q_s = \left (\frac {q}{m} \right ) \right ] of particle.

The above facts are used to accelerate a charged particle in a Cyclotron. This principle is also used in mass-spectrometer or bubble chamber.

Angular frequency of motion

Angular velocity or angular frequency of a particle in circular motion is given by –

\omega = 2 \pi \nu

Therefore, angular frequency of the charged particle will be –

\omega = 2 \pi \times \left ( \frac {q B}{2 \pi m } \right )

= \left ( \frac {q}{m} \right ) B ………… (5)

3. Charge moving in Magnetic Field in angular direction

Consider that, the charged particle enters at an angle ( \theta ) with the direction of magnetic field ( \vec {B} ) as shown in figure.

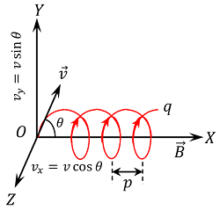
Let, the direction of magnetic field ( \vec {B} ) is along the X axis.

Components of initial velocity of charged particle are –

1. Along X direction -: ( v_x = v \cos \theta ) is the component along the direction of magnetic field.
2. Along Y direction -: ( v_y = v \sin \theta ) is the component perpendicular to the direction of magnetic field.

The charged particle moves with constant velocity of ( v \cos \theta ) along X axis in direction parallel to the direction of magnetic field. Hence, no force acts on the particle in this direction.

But, velocity component ( v \sin \theta ) is perpendicular to the direction of magnetic field. Hence, the particle experiences a force. Due to this force the charged particle tends to move in a circular path in a plane perpendicular to the direction of magnetic field.

Thus, the resultant path of the particle is a helix with its axis parallel to the direction of magnetic field as shown in figure.

Properties of helix motion

Centripetal force required for the particle to move in a circular path is provided by the Lorentz force.

\left ( \frac {mv_x^2}{r} \right ) = q ( v \sin \theta ) B

So, \quad \left [ \frac {m \left ( v \sin \theta \right )^2}{r} \right ] = q ( v \sin \theta ) B

Or, \quad r = \left [ \frac {m { \left ( v \sin \theta \right ) }^2}{q v B \sin \theta} \right ]

= \left [ \frac {m \left ( v \sin \theta \right )}{q B} \right ]

Radius of the circular path of particle is \quad r = \left [ \frac {m \left ( v \sin \theta \right )}{q B} \right ]

= \left [ \frac {\left ( v \sin \theta \right )}{q_s B} \right ] ………. (1)

Time period of the motion of particle is \quad T = \left ( \frac {2 \pi r}{v_x} \right )

= \left ( \frac {2 \pi r}{v \sin \theta} \right )

= \left ( \frac {2 \pi}{v \sin \theta} \right ) r

Putting the value of ( r ) from equation (1), we have –

Therefore, \quad T = \left ( \frac {2 \pi}{v \sin \theta} \right ) \times \left ( \frac {m v \sin \theta}{q B} \right )

= \left ( \frac {2 \pi m}{q B} \right )

= \left ( \frac {2 \pi}{q_s B} \right )

Frequency, of motion of particle is \quad \nu = \left ( \frac {1}{T} \right )

= \left ( \frac {q B}{2 \pi m} \right )

= \left ( \frac {q_s B}{2 \pi } \right )

See numerical problems based on this article.

• P090109