Electric Dipole

What is an Electric Dipole?

A pair of two equal and opposite charges separated by a small distance is called an electric dipole.

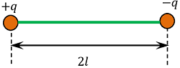
Two equal charges of opposite sign ( + q ) \text {and} ( - q ) , separated by a small distance ( 2 l ) constitute a dipole as shown in figure. The distance between two charges is known as dipole length.

EXAMPLE –

1. Molecules of water ( H_2 O ) , ammonia ( NH_3 ) , Hydrochloric acid ( HCl ) , Carbon dioxide ( CO_2 ) , Sodium chloride ( NaCl ) etc. are examples of electric dipoles.
2. Dipoles are very important for the study of the electric behavior of ionic compounds and their solutions.

Dipole Moment

The product of the magnitude of one of the charge of electric dipole and the dipole length is called dipole moment.

Therefore, dipole moment is –

p = ( q \times 2l )

1. The direction of dipole moment is from negative charge to positive charge.
2. It is a vector quantity.
3. SI unit of dipole moment is coulomb metre ( C \ m ) .

   

One coulomb metre is the dipole moment of a dipole consisting of end charges ( + 1 \ C ) \text {and} ( - 1 \ C ) which are separated by a distance of ( 2l =1 \ m )

Consider about two charges ( + q ) and ( - q ) , which are equal in magnitude but opposite in sign, kept at a small distance of ( 2 \ l ) apart as shown in figure. These to charges together will constitute an electric dipole. Its dipole moment will be p = ( 2 \ q \ l )

Polarity of a Dipole

All matter consists of molecules and these molecules behave as dipoles. These molecules may be of two types.

1. Polar molecule.
2. Non-polar molecule.

Polar molecule

In a molecule, if the centre of mass of positive charge ( i.e. protons ) does not coincide with the centre of mass of negative charge ( i.e. electrons ), then the molecule is said to be a polar molecule.

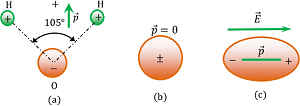
Polar molecules have permanent dipole moment ( \vec {p} ) . A water molecule is a polar molecule as shown in figure (a). The dipole moment of water molecule is ( 6.2 \ \times \ 10^{-30} C \ m ) .

Water being a polar substance acts as a very good solvent for ionic compounds. Ionic compounds when dissolved in water undergoes electrolysis and breaks into ions. A polar molecule is shown in figure ( a ).

Non-polar molecule

If the centre of mass of positive charge ( i.e. protons ) coincides with the centre of mass of negative charge ( i.e. electrons ), then the molecule is said to be a non polar molecule.

The dipole moment of a non-polar molecule is zero. A non-polar molecule is shown in figure ( b ).

When a non polar molecule is placed in a uniform electric field, positive charges experience force in the direction of electric field and negative charge experience a force in a direction opposite to the direction of the electric field. Thus, centres of mass of positive and negative charges displaced in opposite directions and the molecule gets elongated as shown in figure (c). Now it behaves as a dipole.

Therefore, a non-polar molecule becomes a polar molecule under the influence of a strong external electric field.

The dipole moment of such a molecule is called induced dipole moment.

Force on Dipole in uniform Electric Field

When a dipole is placed in an electric field produced by another charged source, it experience a force on it. This force produces a torque on the dipole. The magnitude of the force and torque depends upon following points –

1. The position of dipole with respect to the direction of electric field.
2. Dipole moment of the dipole.
3. Strength of the electric field in which the dipole is kept.
4. Uniformity of the electric field.

Consider about a dipole which is placed in an uniform electric field ( \vec {E} ) , such that the dipole moment ( \vec {p} ) of the electric dipole makes an angle ( \theta ) with the electric field as shown in figure.

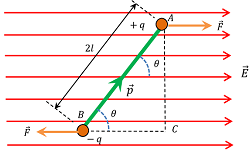
Due to the presence of electric field, the charges ( + q ) and ( - q) of the dipole will experience equal and opposite forces. These forces are given by –

1. \vec {F} = ( + q \vec {E} )
2. \vec {F} = ( - q \vec {E} )

Therefore, net force on the dipole will be –

\vec {F_{net}} = ( + q \vec {E} - q \vec {E} ) = 0

Thus, the net force acting on an electric dipole in a uniform electric field is zero.

But, two equal and opposite forces acting on the dipole will constitutes a couple. This couple will tend to rotate the dipole in the clockwise direction and hence tries to align the dipole along the direction of electric field.

Torque on a Dipole

We know that, torque of a force –

\text {Torque} = \text {Force} \ \times \ \text {Moment arm}

Therefore, torque acting on the dipole will be –

\tau = q E \times AC ……. (1)

From geometry of ( \triangle ABC ) , we will get –

\left ( \frac {AC}{AB} \right ) = \sin \theta

Or, \quad AC = AB \sin \theta = 2 l \sin \theta

Hence, equation (1) becomes –

\tau = q E \times 2l \sin \theta = ( q \times 2l ) E \sin \theta = p E \sin \theta ……. (2)

In vector form, the equation (2) can be written as –

\vec {\tau} = \vec {p} \times \vec {E} ……. (3)

The direction of torque \tau is given by right hand thumb rule.

Torque, when Dipole Moment is parallel to Electric Field

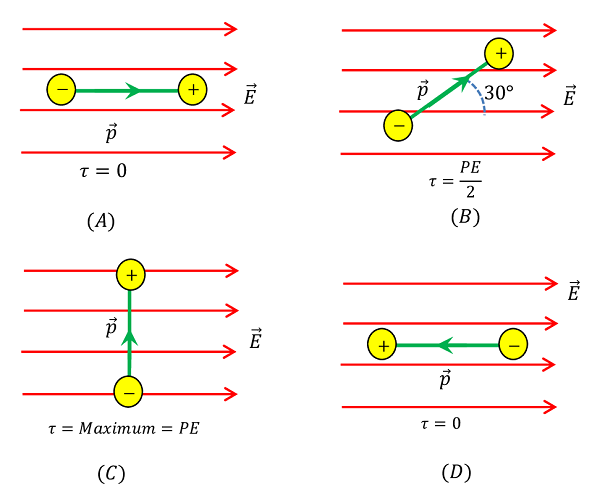
Consider that, the dipole is placed in the field such that the direction of dipole moment is parallel to the direction of electric field i.e. ( \theta = 0 \degree ) . Then, torque acting on the dipole will be –

\tau = p E \sin 0 \degree = 0

Thus, when dipole moment is parallel to the electric field, no torque acts on it. In this case, dipole is in stable equilibrium.

Position of dipole is shown in figure ( A ).

Torque, when Dipole Moment is inclined to Electric Field

Consider that, the dipole is placed in the electric field such that the direction of dipole moment is at an angle ( \theta = 30 \degree ) to the direction of electric field.

Then, torque acting on the dipole will be –

\tau = p E \sin 30 \degree = \left ( \frac {p E}{2} \right )

Thus, when dipole moment is makes an angle of ( 30 \degree ) with the direction of electric field, the torque acting on the dipole is half of the maximum value.

Position of dipole is shown in figure ( B ).

Torque, when Dipole Moment is perpendicular to Electric Field

Consider that, the dipole is placed in the electric field such that the direction of dipole moment is at an angle ( \theta = 90 \degree ) to the direction of electric field.

Then, torque acting on the dipole will be –

\tau = p E \sin 90 \degree = p E

Thus, when dipole moment is at ( 90 \degree ) to the direction of the electric field, torque acting on the dipole is maximum.

Position of dipole is shown in figure ( C ).

Torque, when Dipole Moment is anti-parallel to Electric Field

Consider that, the dipole is placed in the field such that the direction of dipole moment is anti-parallel to the direction of electric field i.e. ( \theta = 180 \degree )

Then, torque acting on the dipole will be –

\tau = p E \sin 180 \degree = 0

Thus, when dipole moment is anti-parallel to the electric field no torque acts on the dipole. Thus dipole is in highly unstable equilibrium.

Position of dipole is shown in figure ( D ).

Force on Dipole placed in Non uniform Electric Field

Consider about a dipole placed in a non uniform electric field \vec {E} as shown in figure.

Let, ( \vec {E_1} ) and ( \vec {E_2} ) are the electric field intensities at position of ( + q ) and ( - q ) charges respectively such that \left ( \vec {E_1} > \vec {E_2} \right ) .

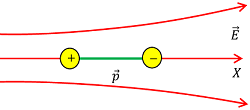
Then, force acting on the end charges of the dipole will be –

1. F_1 = ( + q E_1 )
2. F_2 = ( - q E_2 )

Therefore, net force acting on dipole will be –

F_{net} = ( F_1 + F_2 ) = q ( E_1 - E_2 ) =  q \Delta E ………. (1)

Where, \Delta E = ( \vec {E_1} - \vec {E_2} ) ( Change in electric field ).

Let, length of the dipole is represented as ( \Delta x ) . Then –

p = q \times \Delta x

Therefore, \quad q = \left ( \frac {p}{\Delta x} \right )

Hence, equation (1) can be written as –

F_{net} = \left ( \frac {p}{\Delta x} \right ) \Delta E ………. (2)

In differential form, \quad F_{net} = p \left ( \frac {d E}{d x} \right ) ……… (3)