What is called Parallel Axis Theorem?
If the moment of inertia of a body about an axis is known, then moment of inertia of that body about another parallel axis on the same plane can be obtained by a simple relation called Parallel axis theorem.
Parallel axis theorem is applicable for body of any shape and size. It states that –
Moment of inertia of a body about an axis which is parallel to an axis passing through the centre of mass of the body is equal to the sum of moment of inertia of body about the axis passing through centre of mass and product of area or mass and square of the distance between the two axes.
Consider about a body of area ( A ) as shown in figure.
Axis XX and axis YY are passing through centre of gravity of the body. Let, ( I_{xx} \ \text {and} \ I_{yy} ) are moment of inertia of body about these axes.
Let, OX and OY are another two axes parallel to XX \ \text {and} \ YY axis.

Then, by parallel axis theorem, moment of inertia of the body about OX axis will be –
I_{ox} = I_{xx} + A \left ( y^2 \right )
Similarly, moment of inertia of body about OY axis will be –
I_{oy} = I_{yy} + A \left ( x^2 \right )
See numerical problems based on this article.
Moment of Inertia of rectangular section
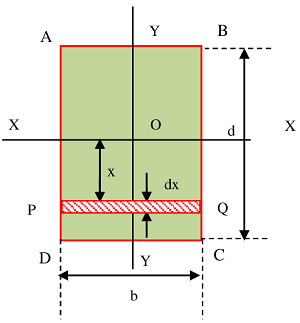
Consider about a rectangular section ABCD as shown in figure. Let, for rectangular section –
- Width ( b ) is parallel to XX axis.
- Depth ( d ) is parallel to YY axis.
- Section is laying on the XY plane.
- Origin lies at the centre of gravity O .
Consider about an elementary strip PQ of thickness ( dx ) .
Area of elementary strip is –
dA = ( b \times dx )
Or, \quad dA = b \ dx
Moment of inertia of elementary strip about XX axis –
d I = [ dA \times \ \text {distance}^2 ]
= ( b \ dx ) ( x )^2 = b \ x^2 \ dx
Therefore, moment of inertia of whole section about XX axis will be –
I_{xx} = \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} dI \right ]
= \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} b \ x^2 \ dx \right ]
= b \left [ \int\limits_{- \frac {d}{2}}^{+ \frac {d}{2}} x^2 dx \right ]
= b \left [ \left ( \frac {x^3}{3} \right )_{- \frac {d}{2}}^{+ \frac {d}{2}} \right ]
= \left ( \frac {bd^3}{12} \right )
Therefore, Moment of Inertia of a rectangular section about XX axis passing through the ( COG ) is given by \quad \left [ I_{xx} = \left ( \frac {bd^3}{12} \right ) \right ] . Where ( d ) is the side of rectangular section perpendicular to the XX axis.
Moment of Inertia of rectangular section about base
Moment of inertia of rectangular section about XX axis is –
I_{xx} = \left ( \frac {bd^3}{12} \right )
By parallel axis theorem, moment of inertia about the base DC will be –
I_{base} = I_{xx} + A \ x^2
Therefore, \quad I_{base} = \left [ \left ( \frac {bd^3}{12} \right ) + ( bd ) \ \left ( \frac {d}{2} \right )^2 \right ]
= \left [ \left ( \frac {bd^3}{12} \right ) + \left ( \frac {bd^3}{4} \right ) \right ]
= \left ( \frac {bd^3}{3} \right )
Therefore, moment of inertia of a rectangular section about its base is given by \left [ I_{base} = \left ( \frac {bd^3}{3} \right ) \right ] . Where ( b ) is the base of rectangular section about which moment of inertia of the body is calculated.
TO BE NOTED –
For calculation of moment of inertia of a rectangular section, cube of that side is taken which is perpendicular to the reference line about which moment of inertia is being calculated.
Moment of Inertia of circular section
Consider about a circle of radius ( r ) , centre O , laying on XY plane as shown in figure.
Let, the axes XX and YY are passing through centre of gravity O .
Consider an elementary circular ring of radius ( x ) and thickness ( dx ) .

Therefore, area of elementary ring is –
dA = 2 \pi \ x \ dx
Moment of inertia of this ring about an axis perpendicular to the plane of section will be –
dI = \text {Area} \ \times \ \text {distance}^2
= ( 2 \pi \ x \ dx ) ( x )^2
= 2 \pi x^3 dx
Therefore, moment of inertia of whole section about an axis perpendicular to the plane of section will be –
I_{zz} = \int\limits_{0}^{r} dI
= \left [ \int\limits_{0}^{r} 2 \pi x^3 dx \right ]
= \left [ 2 \pi \int\limits_{0}^{r} x^3 dx \right ]
= \left [ 2 \pi \left ( \frac {x^4}{4} \right )_{0}^{r} \right ]
= \left ( \frac {\pi r^4}{2} \right )
But, \quad r = \left ( \frac {d}{2} \right )
Therefore, \quad I_{zz} = \left ( \frac {\pi d^4}{32} \right )
Moment of inertia of a circular section about an axis passing through the centre of gravity of the section and perpendicular to the plane of the section is given by \left [ I_{zz} = \left ( \frac {\pi d^4}{32} \right ) \right ] where ( d ) is the diameter of the section.
Moment of Inertia of circular section about diameter
Moment of Inertia of circular section about perpendicular axis through centre of gravity is given by –
I_{zz} = \frac {\pi d^4}{32} .
From perpendicular axis theorem, we know that –
I_{zz} = ( I_{xx} + I_{yy} )
But \quad I_{xx} = I_{yy} ( Due to symmetry ).
Therefore, \quad I_{xx} = I_{yy} = \left ( \frac {1}{2} \right ) \times \left ( I_{zz} \right )
So, \quad I_{xx} = I_{yy} = \frac {1}{2} \left ( \frac {\pi d^4}{32} \right )
= \left ( \frac {\pi d^4}{64} \right )
Therefore, moment of inertia of a circular section about its diameter is \left ( \frac {\pi d^4}{64} \right ) .
Moment of Inertia of triangular section
Consider about a triangular section ABC as shown in figure.
Let, base BC of triangle is ( b ) and its height is ( h ) .
Consider an elementary strip PQ of thickness ( dx ) parallel to the base and at a distance ( x ) from vertex A as shown in figure.

From geometry of figure we have –
\triangle ABC and \triangle APQ are similar.
Hence, by properties of similar triangles, we get –
\left ( \frac {PQ}{BC} \right ) = \left ( \frac {x}{h} \right )
Therefore, \quad PQ = BC \left ( \frac {x}{h} \right ) = \left ( \frac {bx}{h} \right )
Area of the elementary strip will be –
dA = ( PQ \times dx ) = \left ( \frac {bx}{h} \right ) dx
Moment of inertia of this strip about base BC will be –
dI = \text {Area} \ \times \ \text {Distance}^2
= \left ( \frac {bx}{h} \right ) dx ( h - x )^2
= \left ( \frac {bx}{h} \right ) ( h - x )^2 dx
Moment of inertia of the whole section will be –
I_{base} = \int\limits_{0}^{h} dI
= \int\limits_{0}^{h} \left ( \frac {bx}{h} \right ) ( h - x )^2 dx
= \left ( \frac {b}{h} \right ) \int\limits_{0}^{h} x ( h^2 + x^2 - 2hx )dx
= \left ( \frac {b}{h} \right ) \int\limits_{0}^{h} ( xh^2 + x^3 - 2hx^2 ) dx
= \frac {b}{h} \left [ \frac {x^2h^2}{2} + \frac {x^4}{4} - \frac {2hx^3}{3} \right ]_{0}^{h}
= \left ( \frac {bh^3}{12} \right )
Therefore, moment of inertia of a triangular section about its base of is given by \left [ I_{base} = \left ( \frac {bh^3}{12} \right ) \right ] where ( b ) is the base of triangular section and ( h ) is the height.
Moment of Inertia of triangular section about centre of gravity
Moment of inertia of triangular section about its base is given by –
I_{base} = \left ( \frac {bh^3}{12} \right )
Centre of gravity of a triangle lies at \left ( \frac {h}{3} \right ) from its base.
Let, XX is an axis through centre of gravity of triangle and parallel to the base BC .
By parallel axis theorem, moment of inertia about XX axis will be –
I_{base} = I_{xx} + A d^2
Or, \quad I_{xx} = I_{base} - A d^2
NOTE – Here, minus sign is taken because, effective area distribution about XX axis has decreased as compared than effective area distribution about BC .
Therefore, \quad I_{xx} = \left ( \frac {bh^3}{12} \right ) - \left ( \frac {b h}{2} \right ) \left ( \frac {h}{3} \right )^2
= \left ( \frac {bh^3}{36} \right )
Hence, moment of inertia of a triangular section about an axis on the plane of section and parallel to base of triangle and passing through the centre of gravity is given by \left ( \frac {bh^3}{36} \right ) .
See numerical problems based on this article.
