What is called “Conservation of Energy”?
The principle of conservation of mechanical energy states that –
If only the conservative forces are acting on a body, then its total mechanical energy remains constant.
Total mechanical energy possessed by a body may consists of two types of energies –
- Kinetic energy ( K ) .
- Potential energy ( U ) .
Consider that a body undergoes a displacement of ( \Delta x ) under the action of a conservative force, ( F_x ) .
- Then, from work energy theorem, the change in kinetic energy is –
\Delta K = F_x \Delta x .
- For a conservative force, the change in potential energy is given by –
\Delta U = - F_x \Delta x .
From above two equations, we get –
\Delta K = - \Delta U
Or, \quad \Delta K + \Delta U = 0
Therefore, \quad \left ( K + U \right ) = \text {Constant}
Now, if ( K_i ) \ \& \ ( U_i ) are the initial values of kinetic energy & potential energy respectively and ( K_f ) \ \& \ ( U_f ) are the final values of respective quantities of a body, then –
\left ( K_i + U_i \right ) = \left ( K_f + U_f \right )
Hence, in a system of conservative forces, the total mechanical energy of the system is conserved.
Conservation of Energy in falling bodies
Consider that a body of mass ( m ) is laying at position A at a height of ( h ) above the ground level as shown in figure.
As the body falls, its kinetic energy increases gradually and potential energy decreases. That means kinetic energy increases at the expense of its potential energy.
Now, consider about the falling body at various locations during the course of falling.
AT POINT – A
- The body is at rest.
- Thus kinetic energy of the body is ( K_A = 0 )
- Potential energy of the body due to its position from the ground level ( U_A = mgh )
- Therefore, total energy at point A is –
E_A = K_A + U_A = 0 + mgh = mgh
AT POINT – B
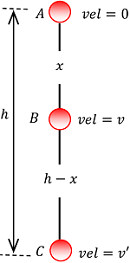
- Suppose the body falls freely through a height ( x ) and reaches the point B with velocity ( v ) .
Then –
v^2 - 0 = 2gx
Or, \quad v^2 = 2gx
- Kinetic energy at point B is –
K_B = \left ( \frac {1}{2} \right ) m v^2 = \left ( \frac {1}{2} \right ) m \times 2gx = mgx
- Potential energy at point B is –
U_B = mg ( h - x )
- Therefore, total energy at point B is –
E_B = ( K_B + U_B ) = [ mgx + mg ( h - x ) ] = mgh
AT POINT – C
- Suppose the body finally reaches to point C on the ground with velocity ( v' ) . Then –
v'^2 - 0 = 2gh
Or, \quad v'^2 = 2gh
- Kinetic energy at point C is –
K_C = \left ( \frac {1}{2} \right ) mv'^2 = \left ( \frac {1}{2} \right ) m \times 2gh = mgh
- Potential energy at point C will be –
U_C = mg ( h - h ) = 0
- Therefore, total energy at point C is –
E_C = K_C + U_C = mgh + 0 = mgh
Clearly, as the body falls its ( PE ) decreases and ( KE ) increases by an equal amount. However, its total mechanical energy i.e. ( KE + PE ) remains constant at all locations.
Hence, total energy of a freely falling body is conserved.
Conservation of Energy in Elastic Spring
Consider about an elastic spring as shown in figure.

- According to Hooke’s law, the spring force for an extension ( x_m ) is given by –
F_s = - \ k x_m
- Work done in stretching the spring will be –
\text {Work done} = \text {Average force} \ \times \ \text {Extension}
When, \quad ( x = 0 ), \quad ( F_s = 0 )
And when \quad ( x = x_m ), \quad ( F_s = - k x_m )
- Therefore, average force in stretching the spring is –
F_{av} = \left (\frac {0 + F_s}{2} \right )
- Work done in stretching the spring from ( x = 0 ) to ( x = x_m ) will be –
W = F_{av} \times x_m
Or, \quad W = \left (\frac {0 + F_s}{2} \right ) \times x_m = \left ( \frac {1}{2} \right ) F_s \times x_m
But \quad F_s = - k x_m
Therefore, \quad W = - \left ( \frac {1}{2} \right ) k {x_m}^2
- Hence, if we stretch a spring to a distance ( x_m ) , its potential energy will be –
U = \left ( \frac {1}{2} \right ) k {x_m}^2 .
When the spring is released, it begins to move under the spring force ( F = - k x ) till it reaches the equilibrium position at ( x = 0 ) where it has got maximum velocity. All its ( PE ) is now converted into ( KE ) .
But due to inertia of motion, the body over shoots the mean position ( x = 0 ) . Now, its velocity decreases until it stops at position ( x = - x_m ) , where all of its ( KE ) is again converted into ( PE ) .
The spring force again pulls the body towards the mean position ( x = 0 )
- Thus the body keeps on oscillating with its total mechanical energy remains constant.
At extreme positions
Here, ( x = \pm \ x_m ) and velocity ( v = 0 ) .
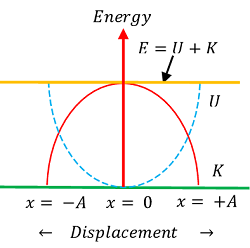
- Kinetic energy \quad K = \left ( \frac {1}{2} \right ) m v^2 = 0
- Potential energy \quad U = \left ( \frac {1}{2} \right ) k x_m^2
Therefore, total energy \quad E = 0 + \left ( \frac {1}{2} \right ) k x_m^2 = \left ( \frac {1}{2} \right ) k x_m^2
At any intermediate position
At intermediate positions, the energy is partly kinetic and partly potential energy.
- Kinetic energy \quad K = \left ( \frac {1}{2} \right ) mv^2 = 0
- Potential energy \quad U = \left ( \frac {1}{2} \right ) k x_m^2
Therefore, total energy \quad E = 0 + \left ( \frac {1}{2} \right ) k x_m^2 = \left ( \frac {1}{2} \right ) k x_m^2
- Variation of ( KE ) and ( PE ) with respect to the position of body is shown in figure.
Conservative Force
A conservative force is defined as a force in which work done by the force is independent of the actual path traveled by the particle between the points.
Consider that a particle moves from a point A to point B by following either of the two paths (1) or path (2) as shown in figure (a).
If the force acting on the particle is a conservative force, then the work done by the force will be the same if the particle moves along path (1) or path (2).

- Therefore, W_{AB} ( along path 1 ) = W_{AB} ( along path 2 )
Now consider about the figure (b). Suppose the particle moves from A to B via path (1) and returns from B to A via path (2).
- Then net work done –
W = W_{AB} ( along path 1 ) \ + \ W_{BA} ( along path 2 )
But, \quad W_{BA} ( along path 2 ) = - \ W_{AB} ( along path 1 )
- Therefore, in a cyclic movement net work done will be –
W = W_{AB} ( along path 1 ) \ + \ W_{BA} ( along path 2 ) = ( W_{AB} - W_{AB} ) = 0
Hence, if the work done by a force in moving a particle around any closed path is zero, then the force is called a conservative force.
Therefore, for conservative forces –
- The work done on a particle doesn’t depend upon the actual path of movement of particle. It depends only on the end points A and B .
- In a cyclic movement, the net work done will become zero, because the particle will return to initial position after completing one cycle.
EXAMPLE –
- Gravitational force, electrostatic force, spring force, elastic force etc. are conservative forces.
- Force of friction and viscous forces etc. are non conservative forces.
Potential Energy & Conservative Force
Potential energy is the energy stored in a body or a system by virtue of its position or by its configuration.
- A conservative force can be defined in terms of potential energy.
Consider that a conservative force ( F_x ) is acting on a particle and the work done is ( W ) .
- By definition, change in potential energy ( \Delta U ) of a system is equal to the negative work done by conservative force on the system.
Therefore, \quad \Delta U = - W
But, \quad W = \int\limits_{x=i}^{x=f} F_x dx
Therefore, \quad \Delta U = - \int\limits_{x=i}^{x=f} F_x dx
Differentiating the equation, we will get –
\left ( \frac {d U_x}{dx} \right ) = - F_x
Or, \quad F_x = - \left ( \frac {d U_x}{dx} \right )
Hence, potential energy ( U ) is defined as a function whose negative gradient gives the magnitude of a force.
Conversely, we may define a conservative force as a force which is equal to the negative gradient of the potential energy ( U ) .
Properties of Conservative Force
- A force ( F ) is called a conservative force if it can be defined as a scalar energy function by the relation \left [ F (x) = \left ( \frac {d U_x}{dx} \right ) \right ] .
- The work done by a conservative force is independent of path and depends only on the end points.
- For a conservative force, work done can be expressed as \left [ W = \int\limits_{x=i}^{x=f} F_x dx = \left ( K_f - K_i \right ) = \left ( U_i - U_f \right ) \right ] .
- The work done by a conservative force is zero if the object moves around a closed path returns to its initial position. Therefore, \left [ W_{(closed \ path)} = \int F_x dx = 0 \right ] .
- If only conservative forces are acting on a body, then its total mechanical energy is conserved.
See numerical problems based on this article.
