What is called Energy?
Energy of a body is defined as the capacity or ability of doing work. Kinetic energy is most important in among all forms of energies.
- Energy is measured by the amount of work that a body can perform.
- Energy and work are mutually interchangeable.
- Hence, all physical quantities like units and dimensions of energy are same as that of work.
There are various forms of energy, such as –
- Kinetic energy. Example – kinetic energy possessed by a moving car, kinetic energy of moving water body etc.
- Potential energy. Example – energy possessed by static water head in dams etc.
- Strain energy. Example – energy possessed by a compressed spring or elongated rubber band etc.
- Light energy. Example – energy of sun light, photoelectric effect etc.
- Electrical energy. Example – electric heater, motor etc.
- Magnetic energy. Example – electromagnets.
- Sound energy. Example – loudspeaker, transducer etc.
- Wind energy. Example – Wind mill etc.
- Pressure energy. Example – bursting of crackers, bombs etc.
- Nuclear energy. Example – nuclear power, atom bomb etc.
Energy in one form can be transformed into another form.
- Kinetic energy.
- Potential energy.
A detail discussion about mechanical energy is done.
Kinetic Energy
The energy possessed by a body due to its motion is called kinetic energy.
- The amount of work that a moving body can do before coming to rest is the measurement of its kinetic energy.
- Similarly, the amount of work required to bring a body from rest into motion is stored in that body as its kinetic energy.
Consider that a body of mass ( m ) is in rest and a force ( F ) is being applied to put it in motion of velocity ( v ) as shown in figure.
- From kinematic equations of motion we have –
( v^2 - u^2 ) = 2as
Since the body was in rest, then initial velocity ( u = 0 ) .
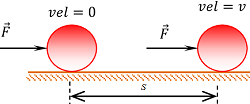
Therefore, \quad ( v^2 - 0 ) = 2as
Or, \quad a = \left ( \frac {v^2}{2s} \right )
- As the force and displacement are in the same direction, so the work done will be –
W = F \ s = m \ a \ s = m \left ( \frac {v^2}{2s} \right ) s = \left ( \frac {1}{2} \right ) mv^2
- This amount of work done will remain stored in the moving body as its kinetic energy.
Therefore, kinetic energy of a moving body of mass, ( m ) moving with a velocity ( v ) is given by –
K = \left ( \frac {1}{2} \right ) m v^2
Relation between Kinetic Energy & Momentum
- By definition of linear momentum, we have –
p = mv
- And, kinetic energy –
K = \left ( \frac {1}{2} \right ) m v^2
= \left ( \frac {1}{2m} \right ) ( m^2 v^2 )
= \left ( \frac {1}{2m} \right ) ( p^2 )
Therefore, \quad K = \left ( \frac {p^2}{2m} \right )
So, \quad p = \sqrt {2mK}
Potential Energy
Potential energy is the energy stored in a body due to its position or by its configuration. It is also called mutual energy or energy of configuration.
- Potential energy is measured by the amount of work that a body or system can do in passing from its present position or configuration to some standard position or configuration called zero position or zero configuration.
Most common types of potential energies are as follows –
- Gravitational potential energy – It is the potential energy associated with the state of separation of two bodies, which attract each other by gravitational force.
- Elastic potential energy – It is the potential energy associated with the state of compression or extension of an elastic object or spring.
- Electrostatic potential energy – It is the potential energy associated with interaction between two static charges.
Power
Power is defined as the rate of doing work.
Therefore, average power is given by –
\text {Average Power} = \text {Work done per unit time}
Or, \quad P_{av} = \left ( \frac {W}{t} \right )
- Power is a ratio of two scalar quantities i.e. work & time, hence it is also a scalar quantity.
Units of Power
Power of an agent is one watt if it does work at the rate of one joule per second.
1 \ \text {watt} = \left [ \frac {1 \ \text {joule}}{1 \ \text {second}} \right ]
Or, \quad 1 \ W = 1 \ \text {J - s}^{-1}
1 \ \text {kW} = 1000 \ \text {W} = 10^3 \ \text {W}
1 \ \text {HP} = 746 \ \text {W} = 0.746 \ \text {kW}
- Commercial unit of electrical power is called “Board of trade” ( BOT ) unit of electrical power. It is kilowatt hour.
One kilowatt hour is the electrical energy consumed by an appliance of 1000 watt for 1 hour.
- Therefore, \quad 1 \ \text {kWh} = 1 \ \text {kW} \times 1 \ \text {hour}
Or, \quad 1 \ \text {kWh} = 10^3 \ \text {W} \ \times 1 \ \text {hour} = 1000 \ \text {Wh}
Or, \quad 1 \ \text {kWh} = 1000 \ \text {J - s}^{-1} \ \times \ 3600 \ s = 3.6 \times 10^6 \ J
- Therefore, \quad 1 \ \text {BOT} = 3.6 \ \times \ 10^6 \ J
See numerical problems based on this article.
