Numericals » 03-Numerical Problems

On: April 12, 2022

“Mechanics” Numerical Problems

Try to solve the following numerical problems based on the topic “Mechanics” to clear the concepts in solving the numerical problems.

First of all go to the theory portion of the respective topic and then try to solve the numerical problems by yourself. If facing problem in solving the numerical, click on the Go to solution button to see the ready made solution placed at the bottom of each numerical problem.

01) PROBLEM – P030101

Two balls are thrown simultaneously. Ball A is thrown vertically upwards with a speed of $( 20 \ m/s )$ from the ground and ball B vertically downwards from a height of $( 40 \ m )$ with the same speed and along the same line of motion. At what points do the two balls collide? Take $( g = 9.8 \ m / s^2 )$

Go to solution –

Keywords related to this problem.

02) PROBLEM – P030102

As soon as a car just starts from rest in a certain direction, a scooter moving with a uniform speed overtakes the car. Their velocity-time graphs are shown in figure.

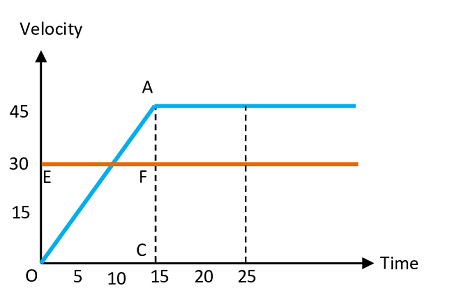
VELOCITY TIME GRAPH OF CAR AND SCOOTER — PROBLEM FIGURE P030102

Calculate (1) the difference between the distance traveled by the car and the scooter in $( 15 \ s )$ (2) the time when the car will catch up the scooter and (3) the distance of car and scooter from the starting point at that instant.

Go to solution –

Keywords related to this problem.

03) PROBLEM – P030103

A bullet is fired into a fixed target loses half of its velocity after penetrating $( 3 \ cm )$ . How much further will it penetrate before coming to rest? Assume that it faces constant resistance to motion.

Go to solution –

Keywords related to this problem.

04) PROBLEM – P030104

The relation between time $( t )$ and distance $( x )$ is $\left ( t = ax^2 + bx \right )$ . Where $( a )$ and $( b )$ are constants. Express the instantaneous acceleration in terms of instantaneous velocity.

Go to solution –

Keywords related to this problem.

05) PROBLEM – P030105

Points $P, \ Q \ \& R$ are in a vertical line such that $( PQ = QR )$ . A ball at point $P$ is allowed to fall freely. What is the ratio of the times of descent through $( PQ ) \ \& \ ( QR )$ ?

Go to solution –

Keywords related to this problem.

06) PROBLEM – P030106

A particle covers half of its total distance with speed $( v_1 )$ and rest half distance with speed $( v_2 )$ . Find its average speed for the whole journey.

Go to solution –

Keywords related to this problem.

07) PROBLEM – P030107

A particle moving along $X$ axis has acceleration $( f )$ at time $( t )$ which is given by the relation $\left [ f = f_0 \left ( 1 - \frac {t}{T} \right ) \right ]$ where $( f_0 ) \ \& \ ( T )$ are constants. Find the velocity of the particle at time $( t = 0 )$ and at the instance when $( f = 0 )$ .

Go to solution –

Keywords related to this problem.

08) PROBLEM – P030108

A person travelling Eastward with a speed of $( 3 \ KMPH )$ finds that wind seems to blow from North. On doubling his speed the wind appears to flow North-east. Find the magnitude of the actual velocity of the wind.

Go to solution –

Keywords related to this problem.

09) PROBLEM – P030109

A string breaks under a load of $( 4.8 \ Kg )$ . A mass of $( 0.5 \ Kg )$ is attached to one end of the string of $( 2 \ m )$ long and is rotated in a horizontal circle. Calculate the greatest number of revolutions that the mass can make without breaking the string.

Go to solution –

Keywords related to this problem.

10) PROBLEM – P030110

Rain is falling vertically with a speed of $( 30 \ m / s )$ . An woman rides a bicycle with a speed of $( 10 \ m / s )$ in the North to South direction. What is the relative velocity of rain with respect to the woman? What is the direction in which she should hold her umbrella to protect herself from rain?

Go to solution –

Keywords related to this problem.

11) PROBLEM – P030111

A ball rolls off the top of a stairway with a constant horizontal velocity $( v )$ . If the steps are $( h \ mtr )$ high and $( w \ mtr )$ wide. Show that the ball will just hit the edge of $( n_{th} )$ step if $\left ( n = \frac {2hv^2}{gw^2} \right )$ .

Go to solution –

Keywords related to this problem.

12) PROBLEM – P030112

Determine the tension in the strings and acceleration of block $A$ and $B$ weighing $( 150 \ Kg )$ and $( 50 \ Kg )$ connected by a string and a friction-less and weightless pulley as shown in figure.

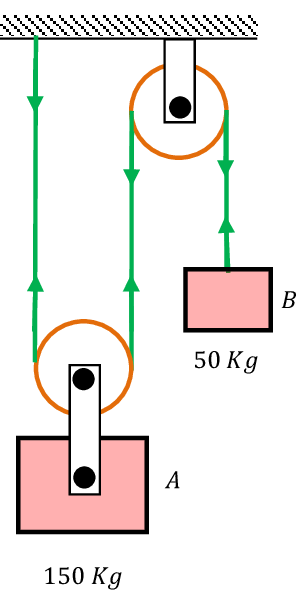
ACCELERATION OF BLOCKS MOVING ON FRICTION-LESS PULLEYS — PROBLEM FIGURE P030112

Go to solution –

Keywords related to this problem.

13) PROBLEM – P030113

An explosion blows a rock into $3$ pieces. Two pieces whose masses are $( 200 \ kg )$ and $( 100 \ kg )$ go off at right angles to each other with a velocity of $( 8 \ m / s ) \ \& \ ( 12 \ m / s )$ respectively. If third piece flies off with a velocity of $( 25 \ m / s )$ then calculate the mass of this piece and find its direction of flight.

Go to solution –

Keywords related to this problem.

14) PROBLEM – P030114

One end of a string of length $( 1.5 \ m )$ is tied to a stone of mass $( 4 \ kg )$ and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at the lower most point so that the string does not slack at any point in its motion along the vertical circle?

Go to solution –

Keywords related to this problem.

Minimum projection velocity of a body for motion in vertical circle.

15) PROBLEM – P030115

An aero plane flying in the sky dives with a speed of $( 360 \ KMPH )$ in a vertical circle of radius $( 200 \ m )$ . The weight of the pilot sitting in it is $( 75 \ kg )$ . Calculate the force with which the pilot presses his seat when the aero plane is (i) at the highest position and (ii) at the lowest position of the circle. Take $( g = 10 \ ms^{-1} )$ .

Go to solution –

Keywords related to this problem.

16) PROBLEM – P030116

A glass marble slides from rest from the topmost point of a vertical circle of radius $( r )$ along a smooth chord. Does the time of descent depend upon the chord chosen?

Go to solution –

Keywords related to this problem.

17) PROBLEM – P030117

Two tall buildings face each other and are at a distance of $( 180 \ m )$ from each other. With what velocity must a ball be thrown horizontally from a window at $( 55 \ m )$ above the ground in one building so that it enters a window $( 10.9 \ m )$ above the ground in the second building?

Go to solution –

Keywords related to this problem.

18) PROBLEM – P030118

A system of masses connected by strings passing over pulleys $A$ and $B$ is shown in figure.

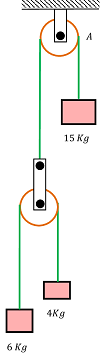
A SYSTEM OF MASS CONNECTED WITH STRING PASSING OVER PULLEY — PROBLEM FIGURE P030118

Find the acceleration of the $3$ masses assuming weightless strings and ideal pulley conditions.

Go to solution –

Keywords related to this problem.

19) PROBLEM – P030119

A projectile is fired horizontally with a velocity of $( 98 \ ms^{-1} )$ from the top of a hill $( 490 \ m )$ high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.

Go to solution –

Keywords related to this problem.

20) PROBLEM – P030120

A ball of mass $( 0.1 \ kg )$ is suspended by a string $( 30 \ cm )$ long. Keeping the string always taut, the ball describes a horizontal circle of radius $( 15 \ cm )$ . Calculate the angular speed.

Go to solution –

Keywords related to this problem.

21) PROBLEM – P030121

A car of mass $( 1500 \ kg )$ is moving with a speed of $( 12.5 \ m / s )$ on a circular path of radius $( 20 \ m )$ on a level road. What should be the frictional force between the car and the road so that the car doesn’t slip? What should be the value of coefficient of friction?

Go to solution –

Keywords related to this problem.

22) PROBLEM – P030122

A hunter aims his gun and fires a bullet directly at a monkey on a tree. At the instant the bullet leaves the barrel of the gun, the monkey drops. Will the bullet hit the monkey? Substantiate your answer with proper reasoning.

Go to solution –

Keywords related to this problem.

23) PROBLEM – P030123

A projectile can have the same range $( R )$ for two angles of projection. If $( t_1 ) \ \& \ ( t_2 )$ are the time of flights in the two cases, then prove that –

$\left ( t_1 . t_2 \right ) = \left ( \frac { 2 R }{ g } \right )$ .

Go to solution –

Keywords related to this problem.

24) PROBLEM – P030124

The radius of a wheel of a car is $( 0.4 \ m )$ . The car is accelerated from rest by an angular acceleration of $( 1.5 \ radian / s^2 )$ for $( 20 \ s )$ . How much distance the wheel covers in this time interval and what will be its linear velocity?

Go to solution –

Keywords related to this problem.

25) PROBLEM – P030125

A particle of mass $( m )$ is released from point $P$ at $( x = x_0 )$ on the $X$ axis from origin $O$ and falls vertically along $Y$ axis as shown in figure.

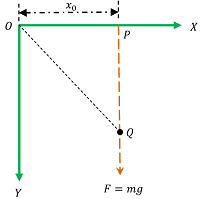
A PARTICLE OF MASS FALLING VERTICALLY — PROBLEM FIGURE P030125

(1) Find the torque acting on the particle at time $( t )$ when it is at point $Q$ with respect to $O$ . (2) Find the angular momentum $( L )$ of the particle about $O$ at this time $( t )$ . (3) Show that particle is following the relation $\left [ \tau = \left ( \frac {dL}{dt} \right ) \right ]$ .

Go to solution –

Keywords related to this problem.

26) PROBLEM – P030126

Calculate the rotational kinetic energy of the earth about its own axis. Mass of the earth is $( 6 \times 10^4 \ kg )$ and radius of the earth is $( 6400 \ KM )$ .

Go to solution –

Keywords related to this problem.

27) PROBLEM – P030127

A meter scale $AB$ is held vertically with its one end $A$ on the floor and is then allowed to fall. Find the speed of the other end $B$ when it strikes the floor. Assume that the end on the floor doesn’t slip.

Go to solution –

Keywords related to this problem.

28) PROBLEM – P030128

A bucket of mass $( 8 \ kg )$ is supported by a light rope wound around a solid wooden cylinder of mass $( 12 \ kg )$ and radius $( 20 \ cm )$ free to rotate about its axis. A man holding the free end of the rope with the bucket and cylinder at rest initially lets go the bucket freely downwards in a well $( 50 \ m )$ deep. Neglecting friction obtain the speed of the bucket and the angular speed of cylinder just before the bucket enters water. Take $( g = 10 \ m / s^2 )$ .

Go to solution –

Keywords related to this problem.

Share this post: