What is meant by Viscosity?
Viscosity is a property of a fluid by virtue of which an internal force of friction comes into play, when the fluid is in motion or tends to be in motion. This frictional force opposes the relative motion between different layers of the fluid.
- A backward dragging force develops in the flowing fluid which is called viscous drag or viscous force.
- This viscous force acts tangentially on the contact layers of the fluid in motion and tends to destroy its motion.
- Effect of Viscosity is felt when the fluid is in motion. Hence, it is also called dynamic viscosity.
Cause of Dynamic Viscosity
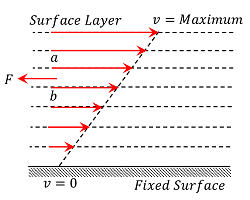
Consider about a liquid moving slowly and steadily over a fixed horizontal surface. The fluid layer which is in contact with the fixed surface is at rest and the velocity of other layers increases uniformly upwards as shown by increasing lengths of arrows in the given figure.
Consider any two adjacent layers ( a ) and ( b ) . The upper layer ( a ) will move faster than the lower layer ( b ) . So, fast moving layer ( a ) will tend to accelerate the lower layer ( b ) , while the slow moving layer ( b ) tends to retard the fast moving layer ( a ) . As a result, a backward dragging tangential force ( F ) will develop. This is called viscous force which tends to destroy the relative motion between these layers. To maintain the motion, an external force is required to be applied to overcome the dragging viscous force.
Coefficient of Viscosity
Coefficient of viscosity of a liquid is defined as the tangential viscous force required to maintain a unit velocity gradient between its two adjacent parallel layers each of unit area.
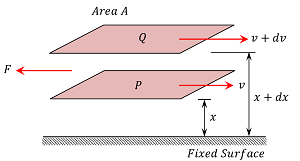
Suppose a liquid is flowing steadily in the form of parallel layers on a fixed horizontal surface as shown in figure.
Velocity gradient
Consider about two adjacent layers P \ \text {and} \ Q at distances ( x ) \ \text {and} \ ( x + dx ) from the fixed surface and moving with velocities ( v ) \ \text {and} \ ( v + dv ) respectively.
Then, \left ( \frac {dv}{dx} \right ) is the rate of change of velocity with distance in the direction of increasing distance and is called velocity gradient.
According to Newton, the force of viscosity ( F ) acting tangentially between two layers is –
(1) Proportional to the area A of the layers in contact.
F \propto A
(2) Proportional to the velocity gradient between the two layers.
F \propto \left ( \frac {dv}{dx} \right )
Therefore, \quad F \propto A \left ( \frac {dv}{dx} \right )
So, \quad F = - \eta A \left ( \frac {dv}{dx} \right )
Here ( \eta ) is the constant of proportionality. It is called coefficient of viscosity of the liquid.
- Coefficient of viscosity depends on the nature of the liquid.
- Negative sign indicates that the viscous force acts in a direction opposite to the direction of motion of the liquid.
If \quad A = 1 \quad \text {and} \quad \left ( \frac {dv}{dx} \right ) = 1
Then, \quad F = \eta ( numerically )
Therefore, co-efficient of viscosity is defined as the –
\eta = \left ( \frac {\text {Tangential viscous force}}{\text {Velocity gradient}} \right ) = \left ( \frac {F / A}{v / x} \right )
Units of coefficient of Viscosity
(1) In CGS system, unit of \eta \ \text {is} \ ( \text {dyne-s-cm}^{-2} ) \ \text {or} \ ( \text {g-cm}^{-1} \text {s}^{-1} ) .
Since, \quad \eta = \left ( \frac {F / A}{v / x} \right ) = \left ( \frac {F}{A}. \frac {x}{v} \right )
Therefore, 1 \ \text {poise} = \frac {1 \text {dyne}}{1 \text {cm}^2} . \frac {1 \text {cm}}{1 \text {cm-s}^{-1}} = 1 \text {dyne-s-cm}^{-2}
The coefficient of viscosity of a liquid is said to be of 1 \ \text {poise} if a tangential force of ( 1 \text {dyne} ) on the surface is required to maintain a relative velocity of ( 1 \text {cm s}^{-1} ) between two layers of the liquid which are 1 \text {cm} apart.
(2) In SI system, unit of \eta \ \text {is} \ ( \text {N-s-m}^{-2} ) \ \text {or} \ ( \text {kg-m}^{- 1} \ s^{-1} ) .
1 \ \text {poiseuille} = \frac { 1 \ \text {N}}{ 1 \ \text {m}^2 }. \frac { 1 \ \text {m}}{ 1 \ \text {m-s}^{-1}} = 1 \ \text {N-s-m}^{-2}
The coefficient of viscosity of a liquid is said to be 1 \ \text {poiseuille or decapoise} if a tangential force of ( 1 \ \text {N} ) on the surface is required to maintain a relative velocity of 1 \text {m-s}^{-1} between two layers of the liquid 1 \text {m} apart.
Relation between poise & poiseuille
We know that –
1 poiseuille or 1 decapoise = 1 \text {N-s-m}^{-2}
= ( 10^5 \text {dyne} ) \times \ s \ \times ( 10^2 \ \text {cm} )^{-2}
= 10 \ \text {dyne-s-cm}^{-2} = 10 \ \text {poise}
Therefore, \quad 1 \ \text {poiseuille} = 10 \ \text {poise}
Kinematic Viscosity
Kinematic viscosity is defined as the ratio of the dynamic viscosity of a fluid to its density.
Therefore, \quad \text {Kinematic viscosity} \ ( \gamma ) = \left ( \frac {\eta}{\rho} \right )
Hence, unit of kinematic viscosity will be \left ( \frac {\text {Unit of dynamic viscosity}}{\text {Unit of density}} \right )
The CGS unit of kinematic viscosity is \left ( \frac {\text {g-cm}^{-1} s^{-1}}{\text {g-cm}^{-3}} \right ) = ( \text {cm}^2 \ \text {s}^{-1} ) .
Effect of temperature
Temperature has different effects on viscosity of a fluid –
FOR LIQUIDS – It decreases with the increase in its temperature.
- When a liquid is heated, the kinetic energy of its molecules increases and the inter-molecular attractions become weaker. Hence, viscosity decreases.
Slotle’s empirical formula for the variation of viscosity of a liquid with temperature is –
\eta_t = \frac {\eta_0}{1 + \alpha t + \beta t^2}
Here ( \eta_t ) \ \text {and} \ ( \eta_0 ) are the coefficients of viscosity at ( t \degree C ) \ \text {and} \ ( 0 \degree C ) respectively, and ( \alpha ) \ \text {and} \ ( \beta ) are constants.
FOR GASES – It increases with the increase in temperature.
- Viscosity of gases is directly proportional to the square root of its absolute temperature.
\eta \propto \sqrt {T}
Effect of pressure
- The viscosity of all liquids increases with the increase in pressure. But, for water, viscosity decreases with the increase in pressure.
- The viscosity of gases is independent of pressure.
Comparison between Viscosity & Friction
Similarities between Viscosity & Friction
Viscosity in fluids and friction in solids has following similarities –
- Viscosity in liquids is similar to friction in solids and converts the kinetic energy into heat energy.
- Both viscous force and solid friction come into action when there is relative motion.
- The strain in a flowing liquid increases with time.
- In solids, the shearing stress is proportional to shear strain. In fluids the shearing stress is proportional to the time rate of change of strain or strain rate.
- So, the coefficient of viscosity of a fluid can be defined as the ratio of shearing stress to the strain rate.
- Co-efficient of viscosity in liquids is given as –
\eta = \left ( \frac {\text {Tangential viscous force}}{\text {Velocity gradient}} \right ) = \left ( \frac {F / A}{v / x} \right )
= \left ( \frac {F / A}{\frac {\Delta x / x}{t}} \right )
= \left ( \frac {\text {Shearing stress}}{\text {Shear strain / t}} \right ) = \left ( \frac {\text {Shearing stress}}{\text {Strain rate}} \right )
And, modulus of rigidity in solids is given as –
\eta = \left ( \frac {F / A}{\Delta x / x} \right ) = \left ( \frac {\text {Shearing stress}}{\text {Shear strain}} \right )
- Thus the coefficient of viscosity of liquids is analogous to the modulus of rigidity of solids.
Dissimilarities between viscosity & friction
Viscosity in fluids and friction in solids has following dissimilarities –
| Sl. No. | Viscous forces | Solid friction forces |
| 1 | Viscous force is directly proportional to the area of layers in contact. | Solid friction force is independent of the area of the surfaces in contact. |
| 2 | It is directly proportional to the relative velocity between the two liquid layers. | It is independent of the relative velocity between two solid surfaces. |
| 3 | It is independent of the normal reaction between the two liquid layers. | It is directly proportional to the normal reaction between the surfaces in contact. |
