How Electric Field develops in a conductor?
Gauss law helps in evaluating the electric field of bodies having continuous charge distribution. It is conveniently used to find the electric field in conductor like a charged wire etc.
As discussed earlier, an electric conductor have a large number of free electrons. These electrons are the carrier of charges. When this conductor is placed in an electric field, these free electrons re-distribute themselves to make the electric field zero at all the points inside the conductor.
Field produced in a solid Conductor
To find the electric field in solid conductor, Gauss law is used as follows.
Consider that, a charged body of conducting material is placed in an electric field as shown in figure. In this case, Re-distribution of free electrons will occur and there will be no field inside the conductor.
Now, consider about a closed surface ( S ) inside the conductor. The electric field associated with this closed surface is zero. Therefore –
\oint\limits_{S} \vec {E}. d \vec {S} = 0
From Gauss law, we know –
\oint\limits_{S} \vec {E}. d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
Therefore, \quad \left ( \frac {q}{\epsilon_0} \right ) = 0
Or, \quad q = 0
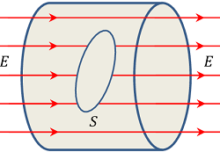
Hence, charge enclosed by the closed Gaussian surface is zero.
Therefore, any volume completely inside a conductor is electrically neutral as there is no electric field.
Now, if a charge is injected anywhere within the conductor, it will come over to the surface of the conductor and settled there on surface.
Therefore, interior of a conductor is always charge free.
Field produced in a hollow Conductor
To find the electric field in hollow conductor, Gauss law is used as follows.
Consider a hollow conductor or a conductor having a cavity as shown in figure. If a charge ( + q ) is injected in the cavity or hole, the inner surface of cavity or hole will get charged by ( - q ) .
By taking Gaussian surface ( S ) as shown in figure, we will find that, electric field ( \vec {E} ) at all points on this surface is zero because total charge enclosed by Gaussian surface becomes zero.
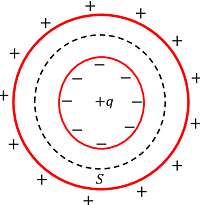
Hence, \quad \oint\limits_{S} \vec {E}. d \vec {S} = 0
Thus, when a charge ( + q ) is placed inside the cavity, there must be a charge ( - q ) developed on the inner surface of the cavity or hole. To counter balance this developed charge, a charge ( + q ) will appear on the outer surface of the conductor as shown in figure.
Thus, we can say that, the injected charge inside the cavity appears at the surface of the conductor. Therefore, interior of a hollow conductor is charge free.
Field produced by a Charged Wire
Consider about a thin straight wire of infinite length uniformly charged with linear charge density ( \lambda ) as shown in figure.
This wire is symmetrical about its axis. Let, we have to find the electric field at any point P which is outside the wire and at a distance ( r ) from the axis of wire.
Consider an imaginary cylindrical surface of radius ( r ) and length ( l ) which will be passing through the point P . This cylindrical surface is the Gaussian surface for this set up.
The charge inside the Gaussian surface is –
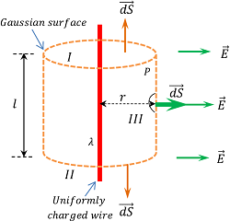
q = ( \lambda l )
According to Gauss law –
\oint\limits_{S} \vec {E} \ d \vec {S} = \left ( \frac {q}{\epsilon_0} \right )
Or, \quad \oint\limits_{S} \vec {E} \ d \vec {S} = \left ( \frac {\lambda l}{\epsilon_0} \right ) …….. (1)
The cylindrical Gaussian surface is consisting of 3 parts as shown in figure. Part (I) and part (II) are the top and bottom circular faces and are perpendicular to the axis of wire.
For these surfaces, angle between ( \vec {E} ) \ \text {and} \ ( d \vec {S} ) \ \text {is} \ ( 90 \degree ) .
So, \quad \vec {E} \ d \vec {S} = E dS \cos 90 \degree = 0
Hence, total flux through the Gaussian surface is only through the curved surface (III). Therefore –
\oint\limits_{S} \vec {E} \ d \vec {S} = \int\limits_{III} \vec {E} . d \vec {S} = \left ( \frac {\lambda l}{\epsilon_0} \right ) …….. (2)
But, direction of electric field vector and surface vector is same i.e. \quad \vec {E} \ d \vec {S} = E . d S \cos 0 \degree
Therefore, \quad \int\limits_{III} E \ d S \cos 0 \degree = \left ( \frac {\lambda l}{\epsilon_0} \right )
Or, \quad \int\limits_{III} E. dS = \left ( \frac {\lambda l}{\epsilon_0} \right )
Since, chosen Gaussian surface is symmetrical about the axis of charged wire, hence electric field intensity ( E ) is constant at every point on the Gaussian surface.
Therefore, \quad E \int\limits_{III} dS = \left ( \frac {\lambda l}{\epsilon_0} \right )
Or, \quad E \times 2 \pi r l = \left ( \frac {\lambda l}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {\lambda}{2 \pi\epsilon_0 r} \right )
Thus, \quad E \propto \left ( \frac {1}{r} \right )
Field produced by a Charged Plane Sheet
Consider about a thin sheet of infinite length uniformly charged with surface charge density \sigma as shown in figure.
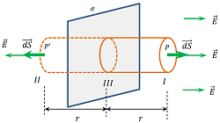
Let, we have to find the electric field at any point P which is outside the sheet and at a distance ( r ) from the plane of sheet.
Consider an imaginary closed cylindrical surface of end cap area ( S ) and length ( r ) located on both sides of sheet. Thus point P will lie on one end cap of the imaginary closed cylinder.
Since, electric field ( \vec {E} ) is normal to the charged sheet. Hence, it will be normal to the end caps also.
The charge inside this Gaussian surface is ( q = \sigma S ) . According to Gauss law –
\oint\limits_{S} \vec {E} \ d \vec {S} = \left ( \frac {q}{\epsilon_0} \right ) = \left ( \frac {\sigma S}{\epsilon_0} \right ) ………. (1)
The cylindrical Gaussian surface is consisting of 3 parts as shown in figure. For curved surface (III), angle between ( \vec {E} ) and ( d \vec {S} ) is ( 90 \degree ) .
So, \quad \oint\limits_{III} \vec {E} \ d \vec {S} = E dS \cos 90 \degree = 0
Therefore, total flux through the Gaussian surface is only through the surface (I) and (II). Therefore –
\oint\limits_{S} \vec {E} \ d \vec {S} = \int\limits_{I} \vec {E} . d \vec {S} + \int\limits_{II} \vec {E} \ d \vec {S} = \left ( \frac {\sigma S}{\epsilon_0} \right ) …….. (3)
Or, \quad \int\limits_{I} E . d S \cos 0 \degree + \int\limits_{II} E . d S \cos 0 \degree = \left ( \frac {\sigma S}{\epsilon_0} \right )
Therefore, \quad \int\limits_{I} E. dS + \int\limits_{II} E. dS = \left ( \frac {\sigma S}{\epsilon_0} \right )
Since, chosen Gaussian surface is symmetrical about the charged sheet, hence electric field intensity is constant at every point of the Gaussian surface.
So, \quad E \int\limits_{I} dS + E \int\limits_{II} dS = \left ( \frac {\sigma S}{\epsilon_0} \right )
Or, \quad ES + ES = \left ( \frac {\sigma S}{\epsilon_0} \right ) .
Or, \quad 2 ES = \left ( \frac {\sigma S}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {\sigma}{2 \epsilon_0} \right )
Therefore, field intensity is not depending upon the distance of point P .
Thus electric field intensity due to infinite sheet of charge is independent of the distance of the point of observation. It only depends upon the surface charge density.
SPECIAL CASE
When, the charged sheet is of considerable thickness, then charge of both sides are taken into consideration.
Then, \quad 2 E S = \left ( \frac {2 \sigma S}{\epsilon_0} \right )
Or, \quad E = \left ( \frac {\sigma}{ \epsilon_0} \right )
