Electric Potential of Dipole

What is the Electric Potential of a Dipole?

Electric potential of dipole at a point in the electric field produced by dipole is defined as the work done by an external force in bringing a test charge from infinity to that point.

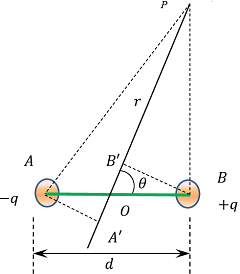
Consider about a dipole $AB$ as shown in figure. Let, –

End charges of dipole are $( - q ) \ \text {and} \ ( + q )$ .
Distance of separation between the charges is $d$ .
$O$ is the mid point of dipole length i.e. $( d = AB )$

Consider about a point $P$ , where $( OP = r )$ and $( \angle {POB} = \theta )$ .

Assume that $( r >> d )$ .

Let, $AA'$ is a perpendicular to $PO$ drawn from point $A$ and $BB'$ is another perpendicular drawn from $B$ .

Therefore, $\quad AP = A'P = ( OP + OA' ) = ( OP + AO \cos \theta ) = ( r + \frac {d}{2} \cos \theta )$

Similarly, $\quad BP = B'P = ( OP - OB' ) = ( r - \frac {d}{2} \cos \theta )$

Potential at $P$ due to the charge $( - q )$ is –

$V_1 = - \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{AP} \right )$

$= - \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r + \frac {d}{2} \cos \theta} \right )$

Potential at $P$ due to the charge $( + q )$ is –

$V_2 = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{BP} \right )$

$= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r - \frac {d}{2} \cos \theta} \right )$

071101 ELECTRIC POTENTIAL DUE TO A DIPOLE

Therefore, net potential at $P$ , due to the dipole is –

$V = ( V_1 + V_2 )$

$= - \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r + \frac {d}{2} \cos \theta} \right ) + \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r - \frac {d}{2} \cos \theta} \right )$

$= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \left ( \frac {q}{r - \frac {d}{2} \cos \theta} \right ) - \left ( \frac {q}{r + \frac {d}{2} \cos \theta} \right ) \right ]$

$= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q d \cos \theta}{r^2 - \frac {d^2}{4} \cos^2 \theta} \right ]$

$= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {q d \cos \theta}{r^2} \right ]$ . Neglecting the term $\left [ \frac {d^2}{4} \cos^2 \theta \right ]$ being very small.

So, $\quad V = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left [ \frac {p \cos \theta}{r^2} \right ]$

Electric Potential of a Point Charge

Consider about a point charge $( q )$ as shown in figure. Let, $P$ is a point at a distance $( x )$ from the charge.

A unit positive charge $( + 1 )$ is placed at $P$ in the electric field produced by the charge $( q )$ . The electrostatic force of repulsion between the charge $( q )$ and charge $( + 1 )$ , will be –

$F = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{x^2} \right )$

$= \left ( \frac {q}{4 \pi \epsilon_0 x^2} \right )$

Direction of force $( \vec {F} )$ is just opposite to the direction of electric field $( \vec {E} )$

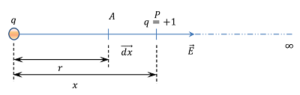
071102 ELECTRIC POTENTIAL OF A POINT CHARGE

Now, let the charge $( + 1 )$ is displaced by a small distance $( dx )$ towards the charge $( q )$ without producing any acceleration.

Small work done in displacing the charge will be –

$dW = \vec {F} . d \vec {x}$

$= F . dx \cos 180 \degree = - F dx$

$= - \left ( \frac {q}{4 \pi \epsilon_0 x^2} \right ) dx$ …….. (1)

Therefore, total work done in displacing the charge from infinity to point $A$ , will be –

$\int {dW} = \int\limits_{\infty}^{r} - \left ( \frac {q}{4 \pi \epsilon_0 x^2} \right ) dx$

Or, $\quad W = - \left ( \frac {q}{4 \pi \epsilon_0} \right ) \int\limits_{\infty}^{ r} x^{(- 2)} dx$

$= - \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {x^{- 1}}{- 1} \right ]_{\infty}^{r}$

$= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {1}{x} \right ]_{\infty}^{r}$

$= \left ( \frac {q}{4 \pi \epsilon_0} \right ) \left [ \frac {1}{r} - \frac {1}{\infty} \right ]$

$= \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r} \right )$

Because, $\quad \left ( \frac {1}{\infty} \right ) = 0$

But, work done in bringing a unit positive charge from infinity to a given point = Electric potential due to the source charge at that point.

Therefore, electric potential at a point at distance $( r )$ from a point charge will be –

$V_{r} = \left ( \frac {1}{4 \pi \epsilon_0} \right ) \left ( \frac {q}{r} \right )$

If the source charge is a positive i.e. $( + q )$ , then electric potential $( V_{r} )$ is positive.
If the source charge is negative i.e. $( - q )$ , then electric potential $( V_{r} )$ is negative.

Variation of Potential with distance

A figure is drawn to illustrate the variation of electric potential at a point with respect to its distance from the source point charge. Two graphs are most important.

Graph of potential versus distance.
Graph of potential versus reciprocal of distance.

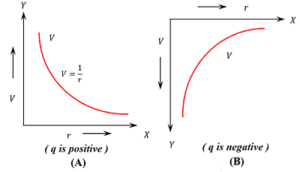
Graph of potential versus distance

Variation of electric potential $( V )$ at a point with respect to its distance $( r )$ from a positive source charge is shown in figure (A).
Variation of electric potential $( V )$ at a point with respect to its distance $( r )$ from a negative source charge is shown in figure (B).

The graph is having following properties.

It is a curve.
Potential is decreasing exponentially with increase in distance $( r )$

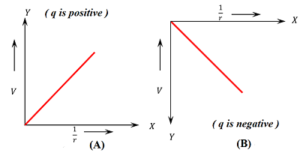
071103 VARIATION OF POTENTIAL WITH DISTANCE

Graph of V versus $\left ( \frac {1}{r} \right )$

Variation of electric potential $V$ at a point with respect to its reciprocal of distance $\left ( \frac {1}{r} \right )$ from a positive point source charge is shown in figure (A).
Variation of electric potential $V$ at a point with respect to its reciprocal of distance $\left ( \frac {1}{r} \right )$ from a negative point source charge is shown in figure (B).

The graph has following properties.