Ideal Gas Equation

What is Ideal Gas Equation?

An equation which gives a relationship between pressure $( P )$ , volume $( V )$ and temperature $( T )$ of any gas, is called Ideal Gas Equation.

Consider about a gas of mass $( m )$ .

According to Boyle’s law $\quad P V = \text {Constant}$
According to Charle’s law $\quad \left ( \frac {V}{T} \right ) = \text {Constant}$

Combining above two relations, we will get –

$\left ( \frac {PV}{T} \right ) = K$

Here, $( K )$ is the constant of proportionality. For one mole of a gas, the constant $( K )$ has the same value for all gases and so, it is called universal gas constant. It is denoted by $( R )$ .

So, gas equation becomes –

$\left ( \frac {P V}{T} \right ) = R$

Or, $\quad P V = R T$ ……… (1)

For $( n )$ number of moles of the gas –

$P V = n R T$ ……… (2)

This equation is called Ideal gas equation or Perfect gas equation.

If $( M )$ is the molecular mass of the gas, then mole number –

$n = \left ( \frac {\text {Mass of gas}}{\text {Molecular mass}} \right ) = \left ( \frac {m}{M} \right )$

Then, ideal gas equation reduces to the form –

$P V = n R T = \left ( \frac {m}{M} \right ) R T$

Or, $\quad P V = m \left ( \frac {R}{M} \right ) T = m k T$

Therefore, $\quad P V = m k T$ ……… (3)

Here, $\quad k = \left ( \frac {R}{M} \right )$ is another constant.

It’s $SI$ unit is $( \text {J-gram}^{-1} K^{-1} ) \ \text {or} \ ( \text {J-kg}^{-1} K^{-1} )$

Also, $\quad P \left ( \frac {V}{m} \right ) = k T$

If $1$ gram of gas is taken then –

$P v = k T$ ………. (4)

Universal Gas Constant

From ideal gas equation for $( n )$ moles of a gas, we have the relation –

$P V = n R T$

Therefore, $\quad R = \left ( \frac {PV}{nT} \right )$

$= \left ( \frac {\text {Pressure} \times \text {Volume}}{\text {Number of moles} \times \text {Temperature}} \right )$

$= \left ( \frac {\text {Work done}}{\text {Number of moles} \times \text {Temperature}} \right )$

Therefore, the universal gas constant represents the work done per mole per Kelvin.

The $SI$ unit of universal gas constant is $\left ( \text {J-mole}^{-1} K^{-1} \right )$ and its $CGS$ unit is $\left ( \text {calorie-mole}^{-1} \degree C^{-1} \right )$

Value of Gas Constant

Consider one mole of a gas at $STP$ , then –

$R = \left ( \frac {P_0 V_0}{T_0} \right )$

We know that –

Standard pressure $( P_0 ) = 0.76 \ m$ of mercury column $= 0.76 \times 13.6 \times 10^3 \times 9.8 \ N m^{-2}$
Standard temperature $( T_0 ) = ( 0 + 273 ) \ K = 273 \ K$
And volume of one mole of gas at $STP \ ( V_0 ) = 22.4 \ \text {litres} = 22.4 \times 10^{-3} m^3$

Therefore, $\quad R = \frac {0.76 \times 13.6 \times 10^3 \times 9.8 \times 22.4 \times 10^{-3}}{273} = 8.31 \text {J-mole}^{-1} K^{-1}$

From mechanical equivalent of heat, the value of $( R )$ in $CGS$ unit system will be obtained after dividing by $\quad j = 4.2$

Therefore, $\quad R = \left ( \frac {8.31}{4.2} \right ) = 1.98 \ \text {cal-mole}^{-1} \degree C^{-1}$

Boltzmann’s Constant

If $( N )$ represents the number of molecules and $( N_A )$ represents the Avogadro’s number for a certain mass of a gas, then –

$\left ( \frac {R}{N_A} \right ) = \text {Constant}$ This is called Boltzmann’s constant. It is represented as $( k_B )$ .

Therefore, $\quad R = k_B N_A$

Value of Boltzmann’s constant is obtained as follows –

$k_B = \left ( \frac {R}{N_A} \right )$

$= \left [ \frac {8.31 \text {J-mole}^{-1} K^{-1} }{6.02 \times 10^{23} \text {mole}^{-1} } \right ]$

$= 1.38 \times 10^{-23} J K^{-1}$

Also, number of moles –

$n = \left ( \frac {\text {Number of molecules}}{\text {Avogadro's number}} \right ) = \left ( \frac {N}{N_A} \right )$

Therefore, using Boltzmann’s constant ideal gas equation can be written as –

$P V = n R T = \left ( \frac {N}{N_A} \right ). k_B N_A. T = k_B N T \quad$

Where $( N )$ is the number of molecules of the gas.

So, $\quad P V = k_B N T$ ………. (5)

Gas Equations

Equation numbers (1), (2), (3), (4) and (5) are the different forms of gas equations. They are used depending upon the given conditions as follows –

Sl. No.	Gas Equation	Gas Constant	Gas Quantity
1	$\quad P V = R T$	Universal gas constant $R = 8.31 \text {J-mole}^{-1} K^{-1}$	One mole of gas.
2	$\quad P V = n R T$	Universal gas constant $R = 8.31 \text {J-mole}^{-1} K^{-1}$	$n$ moles of gas.
3	$\quad P V = m k T$	Gas constant $k = \frac {R}{\text {Molecular mass}}$	$m$ mass of gas.
4	$\quad P v = k T$	Gas constant $k = \frac {R}{\text {Gram Molecular mass}}$	$1$ gram mass of gas.
5	$\quad P v = k_B N T$	Boltzmann constant $k_B = \frac {R}{\text {Avogadros number}} = 1.38 \times 10^{-23} J \ K^{-1}$	$N$ number of molecules of gas.

Ideal Gas

While deriving of the ideal gas equation the following two assumptions are considered –

The size of the gas molecule is so small that it can be neglected.
There is no force of attraction among the molecules of the gas.

However, no real gas fulfill the above two conditions. Hence, the behavior of real gases differ from the ideal gas behavior.

A gas which obeys the ideal gas equation for all values of pressure, volume and temperature is called an ideal gas and a gas which deviate from ideal gas equation is called a Real gas.

Boyle’s Law

Boyle’s law gives a relationship between pressure and volume of a gas at constant temperature.

Boyles law states that, the volume of a given mass of a gas is inversely proportional to its pressure if the temperature remains constant.

Therefore, $\quad V \propto \frac {1}{P}$

Or, $\quad V = K \left ( \frac {1}{P} \right )$

Here, $( K )$ is a constant of proportionality.

Or, $\quad PV = K$

If $( P_1, \ V_1 )$ are the initial values of pressure and volume and $( P_2, \ V_2 )$ are their final values, then –

$P_1 V_1 = P_2 V_2$

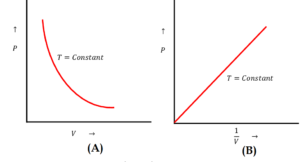
P-V & P-T DIAGRAM OF BOYLE'S LAW — 051501 P-V & P-T DIAGRAM OF BOYLE’S LAW

Figure (A) shows Pressure versus Volume relationship and figure (B) shows Pressure versus Temperature relationship of a gas obeying Boyle’s law.

Charle’s Law

Charle’s law gives a relationship between volume and temperature of a gas at constant pressure.

Charles law states that, the volume of a given mass of a gas is directly proportional to its absolute temperature if the pressure remains constant.

Therefore, $\quad V \propto T$

P-T DIAGRAM OF CHARLE'S LAW — 051502 P-T DIAGRAM OF CHARLE’S LAW

Or, $\quad V = KT$

Or, $\quad \left ( \frac {V}{T} \right ) = K$

Where $( K )$ is a constant of proportionality.

If $( V_1, \ T_1 )$ are the initial values of volume and temperature and $( V_2, \ T_2 )$ are their final values, then –

$\left ( \frac {V_1}{T_1} \right ) = \left ( \frac {V_2}{T_2} \right )$

Following figure shows volume verses temperature relationship of a gas obeying Charle’s law.

If initial conditions of a gas are taken at $( 0 \degree C )$ and final conditions at $( t \degree C )$ , then –

$\left ( \frac {V_0}{T_0} \right ) = \left ( \frac {V_t}{T} \right )$

Or, $\quad V_t = V_0 \left (\frac {T}{T_0} \right ) =V_0 \left (\frac {t + 273}{273} \right )$

For $( 1 \degree C )$ rise in temperature –

$V_1 = V_0 \left (\frac {1 + 273}{273} \right ) = V_0 \left ( 1 + \frac {1}{273} \right )$

$= \left [ V_0 + \left ( \frac {V_0}{273} \right ) \right ]$

Therefore, Charles law can also be expressed as –

If the pressure remains constant then the volume of a given mass of gas increases or decreases by $\left ( \frac {1}{273} \right )$ of its volume at $( 0 \degree C )$ for each $( 1 \degree C )$ rise or fall in temperature respectively.

Gay Lussac’s Law

Gay Lussac’s law gives a relationship between pressure and temperature of a gas at constant volume.

Gay Lussac’s law states that the pressure of given mass of a gas is directly proportional to its absolute temperature if the volume remains constant.

Therefore, $\quad P \propto T$

Or, $\quad P = KT$

So, $\quad \left ( \frac {P}{T} \right ) = K$

Where $( K )$ is the constant of proportionality.

If $( P_1, \ T_1 )$ are the initial values and $( P_2, \ T_2 )$ are final values of pressure and temperature, then –

$\left ( \frac {P_1}{T_1} \right ) = \left ( \frac {P_2}{T_2} \right )$

If initial conditions of gas are taken at $( 0 \degree C )$ and final conditions at $( t \degree C )$ , then –

$\left ( \frac {P_0}{T_0} \right ) = \left ( \frac {P_t}{T} \right )$

Or, $\quad P_t = P_0 \left ( \frac {T}{T_0} \right )$

For $( 1 \degree C )$ rise in temperature –

$P_1 = P_0 \left ( \frac {1 + 273}{273} \right ) = P_0 \left ( 1 + \frac {1}{273} \right )$

Or, $\quad P_1 = \left [ P_0 + \left ( \frac {P_0}{273} \right ) \right ]$

Therefore, Gay Lussac’s law may be expressed in different manner as –

If the volume remains constant then the pressure of a given mass of gas increases or decreases by $\left ( \frac {1}{273} \right )$ of its pressure at $( 0 \degree C )$ for each $( 1 \degree C )$ rise or fall of temperature respectively.

Avogadro’s Law

Avogadro’s law states that –

Under same conditions of temperature and pressure (1) all gases will occupy the same volume and (2) it will contain equal number of molecules.

At $STP$ one mole of every gas will occupy $( 22.4 )$ liters of volume.
It will contain $( 6.0223 \times 10^{23} )$ number of molecules.

Avogadro’s Number

Avogadro’s law further stated that –

The number of particles present in one mole of a substance is $( N_A = 6.0223 \times 10^{23} )$ . This number is called, Avogadro’s number.

In Avogadro’s law the number of particles can be –

Number of atoms present in one gram atom of elements.
Number of molecules present in one gram molecule of compounds.
Number of ions present in one mole of solute in solutions etc.

Dalton’s Law of Partial Pressure

Dalton’s law of partial pressure states that –

The total pressure exerted by a mixture of non reacting gases occupying a given volume is equal to the sum of the partial pressures which gas would exert if it alone occupied the same volume at the given temperature.

Consider about a gas of mass $( m )$ is at pressure $( P )$ and volume $( V )$ . Let it is a mixture of different constituent gases exerting partial pressures $\left ( P_1, \ P_2, \ P_3, \ .... \right )$ etc. then –

$P = \left ( P_1 + P_2 + P_3 + ..... \right )$

Partial Pressure

Partial pressure of a constituent gas in a gas mixture is the pressure which the constituent gas would exert if it alone occupied the total volume at the given temperature.

Let, $\left ( P \right )$ is the pressure of a gas mixture constituting of two gases of mass $\left ( m_1 \right )$ of gas -1 and mass $\left ( m_2 \right )$ of gas – 2.

Also let $\left ( V \right )$ is the volume and $\left ( T \right )$ is the temperature of the gas mixture.

Therefore, total mass of gas mixture $\quad m = \left ( m_1 + m_2 \right )$

And, total pressure of gas mixture $\quad P = \left ( P_1 + P_2 \right )$

Where, $( P_1 )$ and $( P_2 )$ are the partial pressures of the constituent gases in the mixture.

Therefore, $\left ( P_1 \right ) =$ Partial pressure of gas -1. It is the pressure of gas -1 of mass $\left ( m_1 \right )$ , volume $\left ( V \right )$ and temperature $\left ( T \right )$ .

Similarly, $\left ( P_2 \right ) =$ Partial pressure of gas -2. It is the pressure of gas -2 of mass $\left ( m_2 \right )$ , volume $\left ( V \right )$ and temperature $\left ( T \right )$ .

See numerical problems based on this article.