What is Moment Area Method?
Moment area method, is a very convenient way to find slope and deflection of a beam.
It is based on Mohr’s theorem for use of bending moment diagram and enables a quicker solution to find slope and deflection of a beam.
These theorems are stated as follows –
- Mohr’s theorem – 1
- Mohr’s theorem – 2
Mohr’s Theorem – 1
Mohr’s theorem – 1 can be stated as –
Change of slope between any two points on the elastic curve of a beam is equal to the area of bending moment diagram between these points divided by ( EI ) .
PROOF –
Consider about a loaded beam AB whose BM diagram is shown in figure. Now, consider a small element PQ of length ( dx ) of the beam which is at a distance ( x ) from end B .
In figure AP'Q'B is elastic curve of deflected beam. P' and Q' are the corresponding points of element PQ on elastic curve.
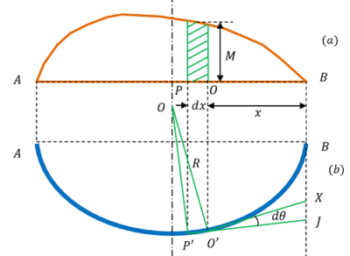
Let, ( R ) is the radius of curvature of bent beam and suppose arc P'Q' subtends an angle ( d \theta ) at the centre of curvature. Then, length of P'Q' will be ( R d \theta )
Since, bending occurs very slightly, so ( P'Q' ) = ( PQ ) = ( dx ) . Therefore, \quad dx = ( R d \theta )
Or, \quad d \theta = \left ( \frac {dx}{R} \right ) …….. (1)
In previous article, from equation of bending stress, we have got the relation –
\left ( \frac {M}{I} \right ) = \left ( \frac {E}{R} \right )
Or, \quad R = \left ( \frac {EI}{M} \right )
Putting this in equation (1) we get –
d \theta = \left ( \frac {dx}{R} \right )
= \left ( \frac {Mdx}{EI} \right )
= \left ( \frac {1}{EI} \right ) M dx ……. (2)
Hence, total change in slope from point A to B , is find by integrating this equation between the limits ( x = l ) to ( x = 0 )
Therefore, expression for the slope will be –
i = \left ( \frac {1}{EI} \right ) \int\limits_{0}^{l} M dx
But, product ( M dx ) represents the area of bending moment diagram shown as shaded area in figure.
Therefore, slope will be –
i = \left ( \frac {\text {Area of BM diagram between A and B}}{EI} \right )
Mohr’s Theorem – 2
Mohr’s theorem – 2 can be stated as –
Intercepts taken on a vertical reference line of tangents at two points on the elastic curve of a beam, is equal to the moment of area of BM diagram about same reference line divided by ( EI ) .
PROOF –
Consider about the BM diagram of the loaded beam as shown in figure. Let P'J and Q'K are two tangents from points P' and Q' respectively, which intersect at points J and K on a vertical reference line drawn from point B .
From geometry of the figure, the tangents at P' and Q' will also meet at an angle ( d \theta ) .
Therefore, length of intercept is –
JK = x \ d \theta = x \left ( \frac {M dx}{E I} \right ) = \left ( \frac {M x dx}{EI} \right )
Total intercept is then find by integrating the above equation between the limits ( x = l ) to ( x = 0 )
Therefore, deflection will be –
y = \left ( \frac {1}{EI} \right ) \int\limits_{0}^{l} M x dx
But, term ( M x dx ) represents the moment of area of the bending moment diagram.
Therefore, \quad y = \left ( \frac {\text {Moment of area of BM diagram between A and B}}{EI} \right )
We will learn in detail about the procedure of application of Mohr’s theorem, to find slope and deflection in beams in following numerical problems.
See numerical problems based on this article.
Conjugate Beam Method
A conjugate beam is defined as an imaginary beam whose – (1) length is equal to the length of original beam (2) width is equal to \left ( \frac {1}{EI} \right ) times the width of original beam (3) loaded with the bending moment diagram of the original beam.
Concept of conjugate beam is used to find the slope and deflection of original beam in a more simpler and convenient way. It is a modified form of “moment area method”, discussed above.
In conjugate beam method, modified Mohr’s theorems are used which may be stated as –
Mohr’s Theorem – 1 (For Conjugate beam)
Shear force at any section of a conjugate beam is equal to the slope of elastic curve at the corresponding section of original beam.
Mohr’s Theorem – 2 (For Conjugate beam)
Bending moment at any section of a conjugate beam is equal to the deflection of elastic curve at the corresponding section of original beam.
We will learn in detail about the procedure of application of “Mohr’s theorem for conjugate beam” to find slope and deflection in numerical problems.
Features of Conjugate beam
Comparative features of an actual beam and its corresponding conjugate beam is tabulated below.
| Sl. No. | Actual beam. | Conjugate beam. | Remarks. |
| 1 | Fixed end. | Free end. | Slope and deflection at fixed end of actual beam is zero. SF \ \& \ BM at free end of conjugate beam is zero. |
| 2 | Free end. | Fixed end. | Slope and deflection at free end of actual beam is zero. SF \ \& \ BM at fixed end of conjugate beam is zero. |
| 3 | Simply supported or roller supported end. | Simply supported end. | Slope at free end of actual beam exists but deflection is zero. SF at simply supported end of conjugate beam exists but BM is zero. |
See numerical problems based on this article.
