Addition of Forces

What is called Addition of Forces?

A body may be subjected upon various forces acting simultaneously upon it. It is very cumbersome and difficult to analyze the effect of each force separately. So, these forces are required to be added together to get the cumulative effect of all the forces acting on that body. This process is called “addition of forces”.

Therefore, addition of forces is a process in which the effect of many forces acting on a body or at a point, are added to express them into the effect of a single force.

The process of adding of two or more forces is also called as “composition of forces”.

Resultant Force

A single force, which we get after addition of many forces by specified rules of vector addition, is called a Resultant Force.

Therefore, the resultant force of two or more forces is defined as that single force which will produce the same effect as if the individual forces together would produce.

Many forces acting at a point are added or subtracted analytically or graphically to find a single resultant force such that the effect of resultant force is same as that of the combined effect of all forces acting on that point.
Since, force is a vector quantity, so its addition or subtraction is carried out as per laws of vector addition.

As a force is a vector quantity, it has magnitude and direction both. So, the forces cannot be added by using simple rules of algebra or arithmetic. Forces can be added by following the rules of addition of vectors in two different methods. These are called as –

Geometrical method of addition of forces.
Analytical methods of addition of forces by resolving them into components.

Laws of Addition of Forces

Many processes are available for addition of forces. These are called as laws of addition of forces. Following are most important Laws for Addition of Forces –

These laws are applicable for both, graphical and analytical methods of addition of forces.

1.Parallelogram Law of Addition of Forces

Among all of the method of addition of forces, parallelogram law of addition of forces is the most convenient way. It is used used to find the resultant of two concurrent forces.

Parallelogram law of addition of forces states that –

If two forces $( \vec { P } )$ and $( \vec { Q } )$ are acting on a point object $O$ are represented in direction and magnitude by two consecutive sides of a parallelogram $OACB$ , then the diagonal of parallelogram passing through the point $O$ will represent the Resultant Force of these two forces.

Magnitude of Resultant Force

Consider about two forces $( \vec { P } )$ and $( \vec { Q } )$ acting at a point $O$ of an object as shown in figure. Let $( \angle { AOB } = \alpha )$ and $( \angle { AOC } = \theta )$ .

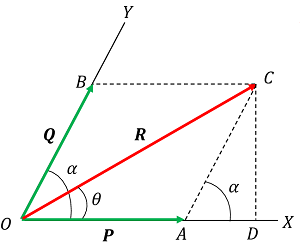
020301 PARALLELOGRAM LAW OF ADDITION OF FORCES

A perpendicular $CD$ is drawn from point $C$ which cuts the extension of side $OA$ at point $D$ .

Since, side $AC$ is equal and parallel to side $OB$ , so $AC = ( \vec {Q} )$

Therefore, $\quad \angle { DAC } = \angle { AOB } = \alpha$

By trigonometric relations, we have –

$AD = Q \cos \alpha \quad$ And $\quad DC = Q \sin \alpha$

Also $\quad OC^2 = ( OD^2 + DC^2 ) = \left [ \left ( OA + AD \right )^2 + DC^2 \right ]$

Therefore, $\quad R^2 = \left [ \left ( P + Q \cos \alpha \right )^2 + \left ( Q \sin \alpha \right )^2 \right ]$

$= \left [ P^2 + 2 P Q \cos \alpha + Q^2 \cos^2 \alpha + Q^2 \sin^2 \alpha \right ]$

$= \left [ P^2 + Q^2 + 2 P Q \cos \alpha \right ]$

Therefore, $\quad R = \sqrt {P^2 + Q^2 + 2 P Q \cos \alpha}$ . This equation gives the magnitude of resultant force $( R )$ .

Direction of Resultant Force

Now let, the resultant force $( R )$ makes an angle $( \theta )$ in positive direction with force $( P )$ .

Then $\tan \theta = \left ( \frac{ DC }{ OD } \right ) = \left ( \frac { Q \sin \alpha }{ P + Q \cos \alpha } \right )$

This equation gives the direction of resultant force $( R )$ with respect to the force $( P )$ .

See numerical problems based on this article.

2.Triangle Law of Addition of Forces

Triangle law of addition of forces is another convenient method to find resultant of two concurrent forces acting on a body. It is stated as –

If two forces $( \vec { P } )$ and $( \vec { Q } )$ are acting on a point object $O$ are represented in magnitude and direction by the two sides of a triangle taken in same order, then their resultant force is represented in magnitude and direction by the third side taken in opposite order.

Consider about two forces $( \vec {P} )$ and $( \vec {Q} )$ acting at a point $O$ as shown in figure.

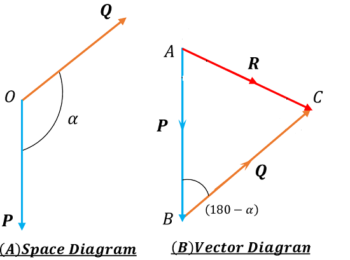
020302 TRIANGLE LAW FOR ADDITION OF FORCES

By taking a suitable scale for magnitude, we can draw a line $AB$ parallel to the force $( \vec {P} )$ which will represent the force $( \vec {P} )$ in magnitude and direction both. Now line $BC$ is drawn starting from point $B$ and parallel to force $( \vec {Q} )$ which will represent the force $( \vec {Q} )$ in magnitude and direction both.

Now, if a triangle $( \triangle ABC )$ is completed by drawing the third side $AC$ , then the magnitude of side $AC$ will give the magnitude of the resultant force $( \vec R )$ and its direction will be from $A$ to $C$ i.e. in reverse order of completing the triangle.

This law is used to find the resultant of two forces only.

Alternative of Triangle Law

In alternate way, triangle law of forces can be expressed as –

If three co-planer and concurrent forces $( \vec P ), \ ( \vec Q )$ and $( \vec R )$ are acting on a body at point $O$ such that it can be represented as sides $AB, \ BC$ and $CA$ of a closed triangle $( \triangle ABC )$ , then body must be in a state of equilibrium.

Consider about a system of three forces as shown in space diagram.

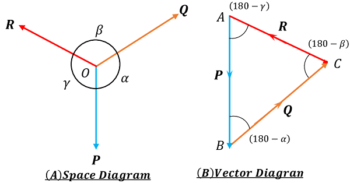
The resultant of two forces $( \vec {P} )$ and $( \vec Q )$ can be obtained from triangle law of forces. It will be $( \vec {R} )$ .

Now if a third force $( \overleftarrow {R} )$ is added in the system which will act in opposite direction of the resultant force $( \vec {R} )$ then these two being equal but opposite in direction will balance to each other.

Thus the body will remain in static equilibrium.

3.Polygon Law of Addition of Forces

Polygon law of addition of forces is used for adding of more than two coplanar and concurrent forces. It is stated as –

If many co-planer forces are acting at a point of a body and if they can be represented by the sides of a closed polygon, then resultant of the forces will be zero and body must be in static equilibrium.

To prove the polygon law of addition of forces, we take the help of triangle law of forces.

Consider that five forces $( \vec {P_1} ), \ ( \vec {P_2} ), \ ( \vec {P_3} ), \ ( \vec {P_4} )$ and $( \vec {P_5} )$ are acting at point $O$ of a body as shown in space diagram.

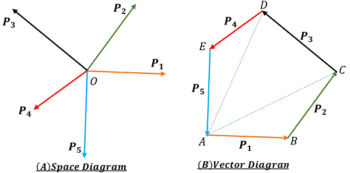
A polygon $ABCDE$ is drawn taking its sides in a scale proportional to these forces. In the polygon we have taken –

Side $AB = ( P_1 )$
Side $BC = ( P_2 )$
Side $CD = ( P_3 )$
Side $DE = ( P_4 )$
Side $EA = ( P_5 )$

Now join $A$ to $C$ and $A$ to $D$ .

By triangle law of addition of forces, we get $AB + BC = AC$ .

Again, $\quad AC + CD = AD$ and $\quad AD + DE = AE$

But, body is subjected to a fifth force $( EA )$ which is just equal in magnitude but opposite in direction to the developed resultant force $( AE )$ .

These two forces, $( AE )$ and $( EA )$ being equal in magnitude but opposite in direction are balancing to each other. Therefore, the resultant of five forces is zero.

Since the resultant of all five forces becomes zero, therefore the body must be in equilibrium. Polygon law is applicable for any number of forces.

See numerical problems based on this article.