Magnetic Effect of Current

What is magnetic effect of current?

If an electric current is passes through a conductor, it start to behave like a magnet. This means that, the current carrying conductor get magnetized due to current flowing through it. This phenomenon is called the magnetic effect of current. If the electric current through the conductor is switched off, it loses its magnetic effect.

Hans Christian Oersted performed a series of experiments and observed that electric current flowing in a conductor produces magnetic effect in the space around itself. This is called magnetic effect of current.

A current carrying conductor produces a magnetic field around itself in a circular fashion. The conductor lies at the centre of this circular magnetic field lines.

The direction of magnetic field lines produced by magnetic effect of electric current can be determined by following rules –

Right hand thumb rule.
Right hand screw rule.

Right Hand Thumb rule

Right hand thumb rule stated as –

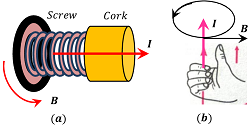
If a conductor carrying current is imagined to be held in the right hand such that the thumb points in the direction of the current, then the tips of the curled fingers encircling the conductor will give the direction of magnetic field lines.

Right hand thumb rule is illustrated in figure ( b ). The conventional representation for a magnetic field coming out of the plane of figure and normal to it is a dot. In other words, the magnetic field perpendicular to the plane in upward direction is denoted by dots. The magnetic field going into the plane of figure in the downward direction and normal to plane is denoted by cross.

Right Hand Screw rule

Right hand screw rule is stated as –

If the forward motion of an imaginary right handed screw is in the direction of current through a linear conductor, then the direction of rotation of the screw gives the direction of magnetic lines of force around the conductor.

Right hand screw rule is illustrated in figure ( a ). This rule is also called Maxwell’s Cork Screw Rule.

Magnetic Force due to Magnetic effect of current

If an static charge i.e. a non-moving charge is placed in a magnetic field, it will experience no magnetic force. But when a moving charge i.e. electric current is placed in a magnetic field, it will experience a magnetic force.

This is explained as below –

Phenomenon associated with stationary charges –
1. When charges are stationary, they only produce electric field around them.
2. Electric field of stationary charges do not affect magnetic fields of near by magnets or magnetic field of conductors carrying current.
Phenomenon associated with moving charges –
1. When charges are moving, they produce magnetic fields as well as electric fields.
2. The magnetic fields produced by moving charges exert forces on magnetic field of nearby magnet or conductors carrying current.

Force on a Single moving charge

Consider about following experiment –

090702 MAGNETIC FORCE ON A MOVING CHARGES

A stationary charge $( q )$ is placed at point $P$ near a metallic wire $AB$ as shown in figure. Wire $AB$ is carrying a current $( i )$ . So, it will produce its magnetic field around it.

Since the charge $( q )$ is stationary, it will experience no magnetic force.

Now, let the charge $( q )$ is projected with certain initial velocity $( v )$ from point $P$ . Because the charge is now moving, it experiences a magnetic force.

By projecting the particle in different directions with different speeds, the following observations are found –

Through point $P$ a line is found such that if the charge is projected along this line, there is no magnetic force.
This line is defined as the direction of the generated magnetic field of the current carrying wire $AB$ .
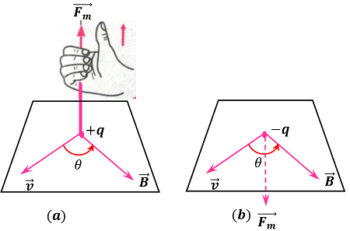
If the direction of velocity $( v )$ of the charge makes an angle $( \theta )$ with this line, then magnitude of the magnetic force $( F_m )$ is found to be proportional to $( v \sin \theta )$ .
The direction of this magnetic force $( F_m )$ is found perpendicular to the direction of the magnetic field as well as to the direction of the velocity.
The magnetic force $( F_m )$ is also proportional to the magnitude of the charge $( q )$ .

This experiment results important information about magnetic field of current carrying wire $AB$ . All of the above facts from (1) to (5) of the above experiment results a definition of the magnetic field of current carrying wire $AB$ . This is –

$\vec {F_m} = q ( \vec {v} \ \times \ \vec {B} )$ …….. (1)

This force $( \vec {F_m} )$ is called magnetic force and the phenomenon is called magnetic effect of electric current.

Directions of magnetic force acting on a positive charge is shown in figure ( a ) and for a negative charge is shown in figure ( b ). These directions of magnetic force are in accordance to the Fleming’s left hand rule.

090703 DIRECTION OF MAGNETIC FORCE ON A MOVING CHARGE

Fleming’s Left Hand rule

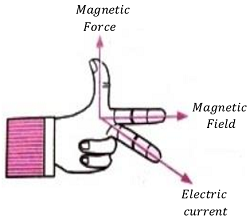
Direction of magnetic force $( \vec {F_m} )$ on a conductor is perpendicular to the plane containing $( \vec {I} )$ and $( \vec {B} )$ and can be determined by using Fleming’s left hand rule.

Fleming’s left hand rule is stated as –

Stretch the left hand such that the fore finger, the central finger and the thumb are mutually perpendicular to each other. When fore finger points in the direction of magnetic field and central finger points in the direction of current , then the thumb gives the direction of the force acting on the conductor.

Fleming’s left hand rule can be applied to determine the direction of magnetic force (1) acting on a charge moving in a magnetic field (2) acting on a conductor carrying current placed in a magnetic field.

Magnitude of Magnetic Field produced by Current

By measuring the magnetic force acting on a moving charge, we can obtain the magnitude of magnetic field $( \vec {B} )$ produced by the wire in which the charge is moving.

The magnetic force is zero when the charge is moving in a direction perpendicular to the direction of magnetic field i.e. when $( \vec {v} \perp \vec {B} )$ .
When the charge is moving in a direction parallel to the direction of magnetic field i.e. when $( \vec {v} \parallel \vec {B} )$ , then magnetic force is $( F_m = q v B )$ .
When the charge is stationary i.e. if $( \vec {v} = 0 )$ , the magnetic force is zero. In this case force $( F_m = q \times 0 \times \vec {B} = 0 )$ .

From equation (1), force on a moving charge will be –

$\vec {F_m} = q ( \vec {v} \ \times \ \vec {B} )$

Therefore, $\quad B = \left ( \frac {F_m}{q \ v} \right )$

This gives the magnitude of magnetic field of a current carrying wire.
The direction of magnetic field $( B )$ is determine by the rules of vector product.

See numerical problems based on this article.