Centre of Pressure

What is called centre of Hydrostatic pressure?

The point at which the resultant hydrostatic pressure acts on the immersed surface is called centre of pressure.

• The intensity of pressure is not uniform at all points on a vertical immersed surface or inclined immersed surface.
• It depends upon the depth of the point below the free liquid surface. As the depth of surface increases, the pressure intensity also increases.
• Hence, the resultant pressure act at a point C which always lies below the centroid G of the surface.
• This point is called the centre of pressure.

Centre of pressure of immersed surfaces

Intensity of hydrostatic pressure at a point on an immersed surface depends upon the depth of that point below the free liquid surface. As the depth of point ( \bar {h} ) increases, the pressure intensity ( p ) also increases.

Therefore, intensity of hydrostatic pressure –

p \ \propto \bar {h}

Therefore, following conclusions can be made –

In vertically immersed surface –

• Average pressure intensity on the area below a horizontal line passing through centroid of the surface will be more as compared to the average pressure intensity on the area above that line.
• Therefore, the centre of pressure ( C ) of a vertically immersed lamina always lies below the centroid ( G ) .

In inclined immersed surface –

• Due to similar reason, average pressure intensity on the area below a horizontal line passing through centroid of the surface will be more compared as compared to the average pressure intensity on the area above the line.
• Therefore, the centre of pressure ( C ) of an inclined immersed lamina also lies below the centroid ( G ) .

In horizontal immersed surface –

• Whole surface area lie at the same depth from the free water surface. Hence, average pressure intensity on the whole area is same.
• Therefore, the centre of pressure ( C ) of a horizontally immersed lamina coincides with the centroid ( G ) .

Centre of pressure of vertically immersed lamina

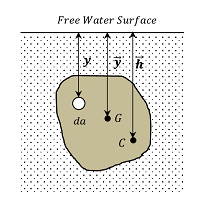
Consider about a vertically immersed lamina as shown in figure.

Let, ( \bar h ) is the depth of point C below the free water surface as shown in figure.

Consider about an elemental area ( da ) of the lamina situated at a depth of ( y ) below the free water surface.

• The total pressure force on the elemental area is  ( w \ y \ da )
• Moment of this force about the water surface will be ( w \ y^2 \ da )

Therefore, moment of the total pressure on the lamina about the water surface will be –

\sum {w \ y^2 \ da} = w \sum {da \ y^2} = w \ I_0

But, ( \sum {da \ y^2} ) represents the moment of inertia of the lamina about the line of intersection of the water surface and the plane of the lamina. Let, it is represented by ( I_0 ) .

• Also total pressure on the lamina is –

P = w \ A \ \bar {y}

This pressure is acting at the centre of pressure C

• Moment of the total pressure about the free water surface will be –

P \ \bar {h} = ( w \ A \bar {y} ) \bar {h}

For equilibrium of the lamina –

( w \ A \bar {y} ) \bar {h} = w \ I_0

So, \quad \bar {h} = \left ( \frac {I_0}{A \bar {y}} \right )

= \left ( \frac {\text {Second moment of the area about the water surface}}{\text {First moment of the area about the water surface}} \right )

Let, ( I_y ) is moment of inertia of the lamina about the centroidal horizontal axis in the plane of the lamina.

By parallel axes theorem of moment of inertia, we get –

I_0 = I_y + A {\bar {y}}^2

Therefore, \quad \bar {h} = \left ( \frac {I_0}{A \bar {y}} \right ) = \left ( \frac {I_y + A {\bar {y}}^2}{A \bar {y}} \right )

= \bar {y} + \left ( \frac {I_y}{A \bar {y}} \right )

Centre of pressure of inclined immersed lamina

An inclined immersed lamina as shown in figure.

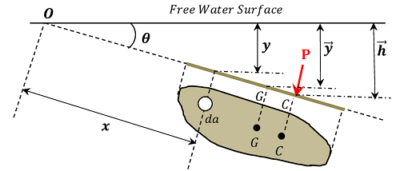
Consider about an elemental area ( da ) of the lamina at a depth ( y ) from free water surface. Force on the elemental area will be –

P = w \ y \ da = w \ da \ x \sin \theta .

This force acts normal to the lamina as shown in figure.

• Moment of this force about O is –

( w \ da \ y ) \times x = w \ da \ x^2 \sin \theta

• Therefore, moment of the total pressure about O will be –

\sum w \ da \ x^2 \sin \theta = w \sin \theta \sum da \ x^2 = w \sin \theta I_0

Here, ( I_0 ) is the moment of inertia of the lamina about the line of intersection of the plane of the lamina and free water surface.

Let, depth of the centre of pressure is ( \bar h ) .

So, distance of point C \text {from point} \ O = \frac {\bar h}{\sin \theta}

• Moment of the total pressure on the lamina about point O will be –

\text {Total pressure} \times \frac {\bar h}{\sin \theta} = w \ A \ \bar y . \frac {\bar h}{\sin \theta}

Therefore, \quad w \ A \ \bar y . \frac {\bar h}{\sin \theta} = w \ \sin \theta \ I_0

Or, \quad \bar h = \frac {I_0}{A \ \bar y} \sin ^2 \theta

Let, ( I_g ) is the moment of inertia of the lamina about centroidal axis in the plane of the lamina parallel to the water surface.

• Distance between the centroidal axis and the water surface is ( \bar y \cosec \theta )

By parallel axes theorem of moment of inertia –

I_0 = I_g + A ( \bar y \cosec \theta )^2 = I_g + A \bar y^2 \cosec^2 \theta

Substituting in the above expression for ( \bar h )

\bar h = \left [ \frac {I_g + A \ \bar y^2 \cosec^2 \theta}{A \bar y} \right ] \sin^2 \theta

= \bar y + \left [ \frac {I_g \sin^2 \theta}{A \bar y} \right ]