What is called simple bending of a beam?
In previous articles, we have discussed about bending moment and different types of loading of beams. Stress developed in a beam depends upon the type of loading.
Simple bending or pure bending is a special condition of loading of a beam in which only bending stress is induced in the section of beam and other type of stresses such as longitudinal stress, shear stress or tangential stress etc. are absent.
Simple bending stress develops only occurs when a beam is loaded with constant bending moment and there is no shear force. In actual conditions, a state of simple bending is difficult to achieve due to self weight of a beam. Because, every beam has weight which produces a shear stress in the beam section.
Therefore, beams are assumed weightless to simplify the process of numerical problems in derivation of equation for bending stress.
Neutral layer
Consider about a small portion ( dx ) of a simply supported beam between two sections AB and CD which is subjected to a sagging bending moment ( M ) as shown in figure.
Due to bending moment, the beam bends in the form of ∪ . Before bending of the beam, these two sections were perpendicular to the longitudinal axis RS . Also, the extreme layers AC and BD were parallel to the RS axis and their lengths were equal as shown in figure.
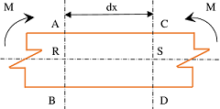
It is evident that, length \quad ( AC ) = ( BD ) = ( RS )
From figure, it is clear that the top layer AC has suffered compression and bottom layer BD has suffered elongation. The layer AC has compressed to A'C' and layer BD has elongated to B'D' .
It is now clear that, in between layers AC and BD there must be a layer RS , which have neither compressed nor elongated. This layer is called neutral layer.

All layers of beam above the neutral layer, will suffer compression and all layers below it, will suffer elongation. Though neutral layer RS has deformed to R'S' but, it has no change in length.
Thus, \quad ( R'S' ) = ( RS )
Neutral layer normally passes through the centre of mass of the beam section.
Bending Stress
Stress developed in a beam section due to a pure bending moment is called bending stress.
Consider about a small length ( dx ) between two sections AB and CD of a simply supported beam subjected to a sagging bending moment ( M ) as shown in figure.
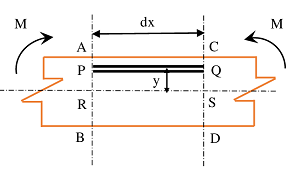
Due to bending moment ( M ) , beam will bend into a curvature. Since the length ( dx ) is very small, the curvature of bending is considered as a circular arc.
Let, radius of curvature of ( dx ) is ( R ) and its centre is at O .
Consider about layers AC \ \text {and} \ BD of beam which has now deformed to A'C' \ \text {and} \ B'D' \ respectively due to bending moment. Consider another layer PQ at a distance ( y ) from neutral layer RS .
Before bending, the layers AC, \ BD, \ RS \ \text {and} \ PQ all were of equal lengths. After bending of the beam, layer AC has compressed, layer BD has elongated and layer RS remain unchanged in length.
Let, decrease in length of layer PQ is ( \delta l ) . Then \quad \delta l = ( PQ - P'Q' )
Therefore, strain of this layer will be –
e = \left ( \frac {\delta l}{l} \right ) = \left ( \frac {PQ - P'Q'}{PQ} \right )
From geometry of curved beam we find that, the two sections ( OP'Q' ) and ( OR'S' ) are sectors of two concentric circles of radii ( R - y ) and ( R ) respectively. The sectors have subtended an angle ( \theta ) at centre O .
Hence, sectors OP'Q' and OR'S' are similar.
So, \quad \left ( \frac {P'Q'}{R'S'} \right ) = \left ( \frac {R - y}{R} \right )

Or, \quad \left [ 1 - \left ( \frac {P'Q'}{R'S'} \right ) \right ] = \left [ 1 - \left ( \frac {R - y}{R} \right ) \right ]
So, \quad \left [ \frac {R'S' - P'Q'}{R'S'} \right ] = \left [ \frac {( R - R + y )}{R} \right ]
= \left ( \frac {y}{R} \right )
Since, ( RS ) is the neutral axis. So, ( R'S' ) = ( RS )
And, before bending of beam ( RS ) = ( PQ )
So, \quad \left ( \frac {R'S' - P'Q'}{R'S'} \right ) = \left ( \frac {PQ - P'Q'}{PQ} \right )
Or, \quad \left ( \frac {PQ - P'Q'}{PQ} \right ) = \left ( \frac {y}{R} \right )
Therefore, strain \quad e = \left ( \frac {y}{R} \right )
Therefore, strain ( e ) of a layer is proportional to its distance ( y ) from neutral axis.
We also know that –
\text {Stress} = \text {Strain} \ \times \ \text {Elasticity} .
Therefore, \quad f = ( e \ \times \ E )
= \left [ \left ( \frac {y}{R} \right ) \times E \right ]
= \left [ y \times \left ( \frac {E}{R} \right ) \right ]
So, \quad \left ( \frac {f}{y} \right ) = \left ( \frac {E}{R} \right )
This equation is known as Equation for Bending Stress.
Since, ( E ) and ( R ) are constants, therefore bending stress ( f ) on a layer is proportional to its distance ( y ) from the neutral axis.
Therefore, \quad f \propto y
Neutral Axis
The line of intersection of neutral layer with any normal cross section of a beam is known as neutral axis.
Consider about a transverse cross section of a rectangular section beam as shown in figure. Let NS is the neutral axis of the section.
Now consider a small layer PQ of area ( \delta a ) at a distance ( y ) from neutral axis. Intensity of bending stress on this layer will be –

f = y \left ( \frac {E}{R} \right )
Therefore, total resistance offered by the layer PQ will be –
\text {Resistance} = \text {Stress} \ \times \ \text {Area}
= ( f \times \delta a ) = \left [ y \left ( \frac {E}{R} \right ) \delta a \right ]
Beam is in equilibrium. Therefore, sum of total resistance over whole section ( i.e. above and below the neutral axis ) must be zero.
So, \quad \sum { \left [ y \left ( \frac {E}{R} \right ) \delta a \right ]} = 0
Or, \quad \sum { \left [ \left ( \frac {E}{R} \right ) ( y \delta a ) \right ]} = 0
But, \left ( \frac {E}{R} \right ) is a constant. Therefore, \quad \sum {( y \delta a )} = 0
But –
- ( y \delta a ) represents the moment of small area ( \delta a ) about neutral axis.
- And ( \sum y \delta a ) represents the moment of whole area of section about neutral axis.
Therefore, it is concluded that neutral axis is so located that moment of whole area of section about this axis must equals to zero. This condition will be true only with the centroid of any section.
Therefore, neutral axis of any beam section passes through centroid or centre of gravity of that section.
See numerical problems based on this article.
