What is called a Projectile Motion?
When a particle is thrown in space near the earth’s surface then it moves along a curved path under the influence of gravity, then its motion is called a projectile motion.
In a projectile motion –
- Particle thus thrown is called a projectile.
- The curved path traced by the projectile motion is called its trajectory.
- The trajectory of a projectile motion is a parabolic curve shown by Galileo.
- If the particle is thrown vertically upward, it will return back moving on same path. Then its trajectory will be a vertical straight line.
- In the absence of air resistance, the motion of a projectile is considered as the combination of two independent motions – (1) motion along horizontal direction with constant velocity and (2) motion in vertical direction with constant acceleration of ‘g’. This is called “principle of independence of motions”.
EXAMPLES OF PROJECTILE MOTION –
- A javelin thrown by a player.
- A jet of water coming out from the side hole of a vessel.
- A stone thrown horizontally from the top of a building.
Principle of Independence of Motions
In the absence of air resistance, the motion of a projectile is considered as the combination of following two independent motions –
- Motion along horizontal direction with uniform velocity.
- Motion along vertical direction with uniform acceleration equal to acceleration due to gravity, ( g ) .
The above two motions ( i.e. motion in horizontal and vertical directions ) of a projectile are independent of each other. This is called the principle of physical independence of motions.
EXAMPLE –
The principle of physical independence of motion can be understood with the following example –
- If a ball A is dropped downward from the roof of a building and at the same time from the same place another ball B is thrown in a horizontal direction, then both the balls will reach the ground at different places but at the same time.
- It proves that the vertical motion of ball B is not affected by its horizontal motion.
Angular projection from ground
Consider about a body which is projected with initial velocity ( u ) from a point O on the ground level at an angle ( \theta ) with the horizontal as shown in figure.
The initial velocity ( u ) of body has two rectangular components –
- Horizontal component ( u \cos \theta ) .
- Vertical component ( u \sin \theta ) .
Equation of Trajectory
The equation of the path traversed by a projectile is called equation of trajectory.
Suppose, the body reaches the point P after time ( t ) .
Horizontal motion has no acceleration. Thus, using kinematic equation, horizontal distance covered will be –
x = u \cos \theta t
Or, \quad t = ( \frac { x }{ u \cos \theta } )
Vertical motion has constant acceleration ( g ) . Thus, distance covered will be –
y = ( u \sin \theta ) t - \left ( \frac {1}{2} \right ) g t^2
= ( u \sin \theta ) \left ( \frac {x}{u \cos \theta} \right ) - \left ( \frac {1}{2} \right ) g \left ( \frac {x}{u \cos \theta} \right )^2
= \left ( \tan \theta \right ) x - \left ( \frac {g}{2 u^2 \cos^2 \theta} \right ) x^2
In this equation, ( \theta, \ u \ \text {and} \ g ) are constants. Thus,
- Term \left ( \tan \theta \right ) is a constant, let it is ( p )
- Term \left [ \left ( \frac {g}{2 u^2 \cos^2 \theta} \right ) \right ] is also a constant, let it is ( q )
So, \quad y = p x - q x^2
Therefore, ( y \propto x^2 ) , which is a required condition of a parabola.
Therefore, the trajectory of the projectile is a parabola.
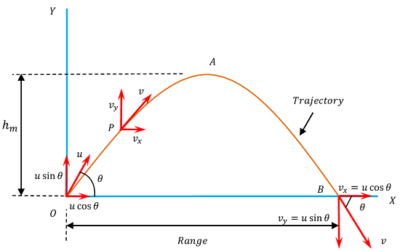
Time of Maximum height
As the body is projected it goes up. Vertical component of velocity ( u \sin \theta ) gradually diminishes and becomes zero at the maximum height of flight. After that, body starts moving downwards.
Let, ( t_m ) is the time to reach at maximum height ( h_m ) of flight.
Therefore, from kinematic equation, we have –
0 = u \sin \theta - g t_m
Or, \quad t_m = \left ( \frac {u \sin \theta}{g} \right )
Time of Flight
Total time taken by the projectile between the instant it is projected and till it reaches at a point in the horizontal plane of its projection is called Time of flight.
Let, the body reaches at point B on ground after time ( T_f ) of projection. Then –
Net vertical displacement covered during the time of flight is zero. Using kinematic equation of motion, we get –
0 = ( u \sin \theta ) T_f - \left ( \frac {1}{2} \right ) g \ ( T_f )^2
Or, \quad T_f = \left ( \frac {2 u \sin \theta}{g} \right ) = 2 \left ( \frac {u \sin \theta}{g} \right )
= 2 t_m
Thus, \quad \text {Total time of flight} = \text {Time of ascent} + \text {Time of descent}
= 2 \times \text {Time of maximum height.}
Maximum height of Flight
It is the maximum height reached by a projectile. It is denoted by ( h_m ) .
At the highest point of flight, the vertical component of velocity becomes zero.
From kinematic equation of motion, we have –
v^2 = u^2 + 2 a s
Therefore, \quad 0^2 - ( u \sin \theta )^2 = 2 ( - g ) h_m
Or, \quad h_m = \left ( \frac {u^2 \sin^2 \theta}{2 g} \right )
Horizontal Range
Horizontal distance traveled by a projectile during its total time of flight is called Horizontal Range.
\text {Horizontal range (R)} = \text {Horizontal velocity} \times \text {Time of flight}
So, \quad R = ( u \cos \theta ) \times 2 \left ( \frac {u \sin \theta}{g} \right ) = \left ( \frac {u^2}{g} \right ) ( 2 \sin \theta \cos \theta )
= \left ( \frac {u^2 \sin 2 \theta}{g} \right )
See numerical problems based on this article.
Horizontal Projection from Height
Consider about a body projected horizontally with initial velocity ( u ) from a point O at a height ( h ) above the ground level as shown in figure.
The body is under the influence of two independent motions –
- Uniform horizontal velocity ( u ) .
- Vertical downward accelerated motion with constant acceleration ( g ) .
Under the combined effect of these two motions, the body moves along a curved path OPA .
Trajectory of Projectile

After time ( t ) , suppose the body reaches at point P .
Acceleration in horizontal direction is zero and initial velocity is ( u ) . Using kinematic equation, the horizontal distance covered by the body will be –
x = u t
Or, \quad t = \left ( \frac {x}{u} \right )
Acceleration in vertical direction is ( g ) but initial velocity is zero. Using kinematic equation, vertical distance traveled will be –
y = 0 \times t + \left ( \frac {1}{2} \right ) g t^2
Putting the value of time \left ( t = \frac {x}{u} \right ) \quad , we get –
y = \left ( \frac {1}{2} \right ) g \left ( \frac {x}{u} \right )^2 = \left ( \frac {g}{2u^2} \right ) x^2
But, \left ( \frac {g}{2u^2} \right ) is constant because u \ \text {and} \ g are constants.
So, \quad y = k x^2
Therefore, ( y \propto x^2 ) , which is a required condition of a parabola.
Therefore, the trajectory of the projectile is a parabola.
Time of Flight
Total time for which a projectile remains in space is called its time of flight.
Let, ( T ) is the time of flight.
Consider vertical motion of body. Using kinematic equation, we will get –
h = 0 \times T + \left ( \frac {1}{2} \right ) g T^2
Therefore, \quad T = \sqrt { \left ( \frac {2h}{g} \right ) }
Horizontal Range
Total horizontal distance covered by the projectile during time of flight is called horizontal range. It is equal to OA = R .
\text {Horizontal range (R)} = \text {Horizontal velocity} \times \text {Time of flight}
Or, \quad R = u \times T
Putting the value of T = \left [ \sqrt { \left ( \frac {2h}{g} \right ) } \right ] , we will get –
R = u \sqrt { \left ( \frac {2h}{g} \right ) }
Velocity at an instant
At any instant ( t ) , let the body is at point P and its velocity is ( v ) .
This velocity has two rectangular components –
- Horizontal component ( v_x = u )
- Vertical component ( v_y = 0 + gt = gt )
Therefore, resultant velocity at point P is –
v = \sqrt { ( v_x )^2 + ( v_y )^2 } = \sqrt { ( u^2 + g^2 t^2 ) }
If the velocity ( v ) makes an angle ( \beta ) with the horizontal, then –
\tan \beta = \left ( \frac {v_y}{v_x} \right ) = \left ( \frac {g t}{u} \right )
Or, \quad \beta = \tan^{-1} \left ( \frac {g t}{u} \right )
See numerical problems based on this article.
